运筹规划(零)-运筹优化基础

运筹学是一本规划数学，是数学建模的基础课程之一，本文将介绍一些和运筹学相关的知识。

如果解决一个问题

十分简单没有任何反直觉的步骤，我们尽量通过一些经典的运筹学问题来讲解这门科学。

有一家工厂有三个厂房，厂房1制作铝框架和硬件，木制框架给厂房2生产，厂房3负责玻璃产品和组装。最近发现市场上有几个比较大的产品新产品。

很明显，产品需要厂房1和3，而产品需要厂房2和3，那么问题来了如何让收益最大化呢。

先来看以下这个表格，根据收集的数据

工厂	每批产品1生产时间	每批产品2生产时间	每周可用小时数
1	1	0	4
2	0	2	12
3	3	2	18
每批利润	3000	5000

首先我们来定义这个问题是一个生产组合问题，是一个线性规划问题，然后我们根据步骤建立数学模型。

我们来定义如下变量, $x_1=每周生产产品1的批次$ ， $x_2=每周生产产品2的批次$ ， $Z=每周生产产品的总利润(千美元)$

很容易写出计算公式。

Z=3x_1+5x_2 \tag{1.1}

我们需要求 $x_1,x_2$ ,让Z最大，Z就是我们经常提到的目标函数。我们根据实际情况将一些情况受限制条件列出来。

x_1<=4 \tag{1.2}

2x_2<=12\tag{1.3}

$3x_1+2x_2<=18 \tag{1.4}$

x_1>0 , x_2>0 \tag{1.5}

我们来看看上面这个表达式的约束，对照表格十分好理解是不是，接下来我们就是要解这个模型，从而获得符合条件的目标函数。

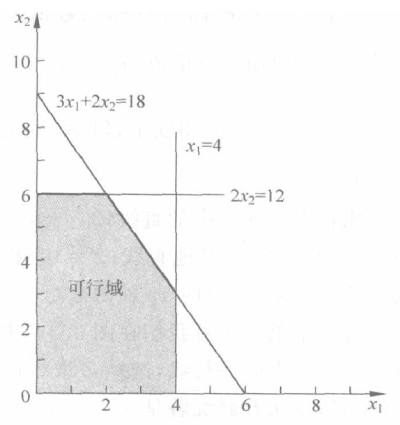
我们将所有受到限制的条件都画到一个坐标系中，如上图。我们很容易的构建了一个可行域。通过这个可行域我们来看我们的目标函数。

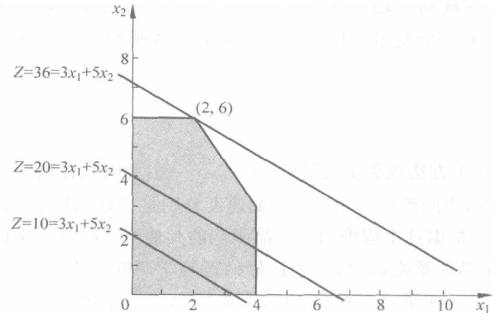
我们的问题就是在可行域内找到一个能让Z最大的取值。这个时候你是不是有个疑问，你画的线怎么都是平行的，这是为啥，我明明有无数种画法，好我们来解决这个问题。我们来看公式1.1与下面的公式不是等价

x_2=-\frac{3}{5}x_1 + \frac{1}{5}Z \tag{1.6}

很明显我们的 $`$ \frac{3}{5} $`$ 就是这个表达式的斜率，并且是一个定值，也就是上图画的。我们使用这个斜率平行滑动，在可行域的边界找到了这个最大值。好了一不小心给解啦。

通过上面这个例子我们来给出线性规划的一般形式

max\ Z=c_1x_1+c_2x_2+..+c_nx_n

st.\ a_ix_i<b_1 ...

等等，这样的表达就是线性规划的标准形式，接下来我们会将更多关于线性模型的知识。