今天这章主要介绍一些聚类算法。
无监督算法相信大家工作中用到的并不是很多,这里先来宏观上介绍一下无监督算法的相关知识。
随机性判断
随机性判断是指当我们拿到一份数据的时候,首先要判断一下这个数据是否适合聚类,如果数据分布不适合聚类就没必要进行下一步的动作啦。
霍普金斯统计量
随机性判断是最经典的指标就是霍普金斯统计量,这个指标主要是告诉我们数据集R遵循空间的均匀分布的概率。从聚类视角来看,它可以评估给定数据集合是或否存在聚类的必要性,所以我们希望数据是非均匀分布的,才有聚类的必要性。
计算步骤
在数据集合R中随机抽取n个点p1,...,pn.对每个点pi,我们找到pi在R中的最近邻的pj,并令xi为pi和pj之间的距离
在数据集R的定义域中随机生成n个点q1,...,qn,将构成的数据集记为R’,对每个点qi,我们找出qi在R′−qi中的最邻近的点qi−j,并另yi为qi与qi−j之间的距离。霍普金斯统计量计算的方式如下
H=∑i=1nxi+∑i=1nyi∑i=1nyi
如果R是均匀的∑i=1nxi,∑i=1nyi将会很接近,因而H大于为0.5.如果R 倾斜的,H将接近于1.
类簇的选择
对于一个存在聚类趋势的数据,类簇的数量是决定算法的重要因素,接下来咱们一起看看哪些指标是选择类簇的指标。
误差平方和(SSE)
SSE=i=1∑nwi∣yi−H(x)i∣2
这个指标一般实际计算回归算法的整体误差,这里可以计算聚类误差,但是要做一些修改。
SSE=k=1∑mi=1∑nwi(yi−Ck)2
其中Ck表示每个类簇中心,m表示类簇的数量,这里的误差不是预测值和真实值的误差,而是样本与类簇中心的距离。当类簇数量变化时,误差平方也会随着变化,一般情况下类簇越多,误差平方越小,当类簇数量等于样本数量的时候,误差平方为0.在误差平方和随着类簇数量增多变化的过程中,有一个下降最快的方向,一般称为肘点。
l另一个反应类簇数量和聚类效果的叫做轮廓系数。
si=max∣a(i),b(i)∣b(i)−a(i)
其中a(i)表示类簇内的近距离,b(i)表示簇间的距离,s(i)取值间是正负一之间。轮廓系数越大,说明内聚性好。轮廓系数不仅能给出合理的类簇数量,同时也反应出聚类得效果。
Kmeans
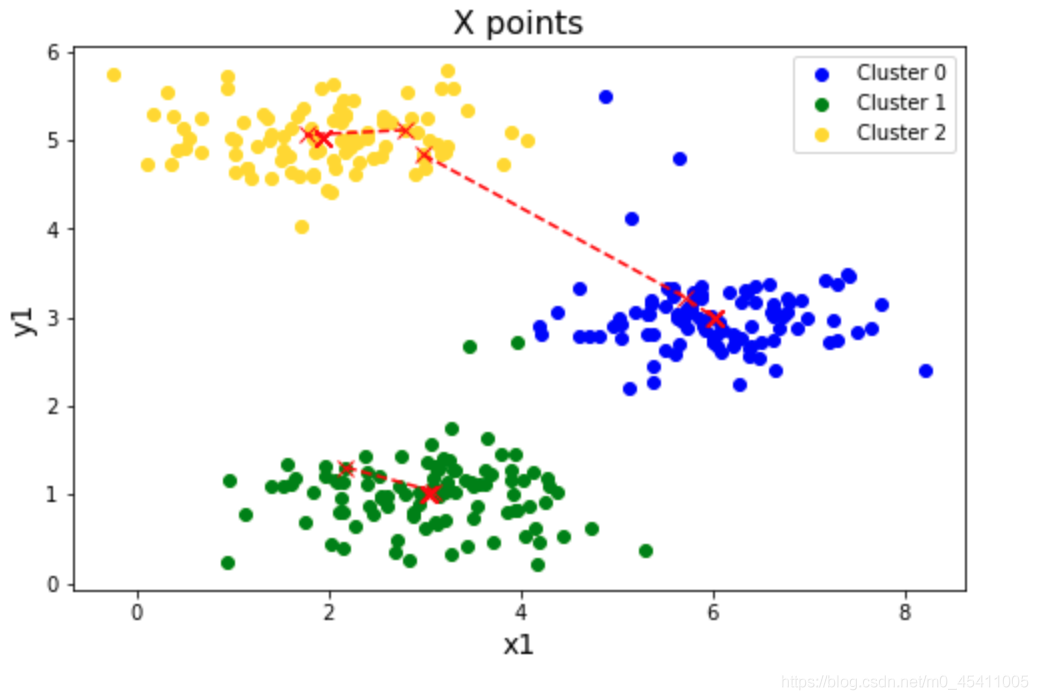
Kmeans的算法思路十分简单,主要有以下的一个步骤。
1. 分配数据点到最近的簇心所在的簇中。
2. 重新计算每个簇的簇心,即将同一簇中所有数据点的坐标取平均值,得到新的簇心。
Kmeans优点
K-Means算法的优点是简单、易于实现,同时适用于大规模数据集。
缺点是需要事先指定聚类数量K,且对初始选取的簇心较为敏感,容易陷入局部最优解。因此,K-Means算法通常需要多次运行,并选择最优的聚类结果。
K-Means算法聚类的结果一般会成圆形,这种结果是因为聚类的方法决定的。
DBScan
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,可以自动识别数据中的噪声点,并将数据点分为不同的簇。相比于K-Means等算法需要预先指定簇的数量,DBSCAN能够自适应地确定簇的数量,同时具有较好的鲁棒性和可扩展性。
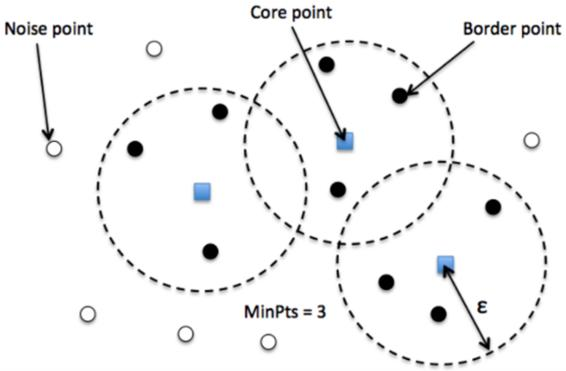
DBSCAN算法的基本思路是,对于每个数据点,以其邻域内的其他数据点密度作为判定标准,将其划分为核心点、边界点或噪声点。然后,以核心点为中心,不断扩张邻域,将所有密度可达的点划分为同一簇。最终,所有不属于任何簇的噪声点会被单独标记出来。
DBSCAN算法特点
DBSCAN算法的优点是能够处理任意形状的簇,对初始值不敏感,且能够识别噪声点。
缺点是需要手动调整两个参数:邻域半径和最小密度,同时对高维数据的聚类效果不如低维数据。
这里需要解释一下,DBSCAN算法在高维数据上的聚类效果不如低维数据,主要原因是高维空间中的数据点之间的距离变得很稀疏,即所谓的“维数灾难”问题。在高维空间中,数据点的密度会呈现出非常稀疏的分布,这就导致DBSCAN算法很难确定合适的邻域半径和最小密度参数。
因此,在高维数据中进行聚类分析时,需要考虑采用其他的聚类算法或者对数据进行降维处理,以获得更好的聚类效果。
DBSCAN算法对于密度较高的异常值具有一定的容忍度,但对于密度较低的异常值仍然是敏感的。
分层聚类
层次聚类算法(Hierarchical Clustering)是一种基于距离的聚类算法,它的主要思想是将数据样本逐步合并成越来越大的簇,直到所有样本都被合并为一个簇或者满足某个停止准则为止。层次聚类算法可以分为两种:凝聚层次聚类和分裂层次聚类。
凝聚层次聚类的基本思路是,首先将每个样本看作一个初始簇,然后将距离最近的两个簇合并成一个新簇,重复该过程直到所有样本都被合并为一个簇或者满足某个停止准则为止。
分裂层次聚类的基本思路是,首先将所有样本看作一个初始簇,然后将簇中距离最远的样本拆分成两个簇,重复该过程直到满足某个停止准则为止。
层次聚类算法的优点是能够自动确定聚类数量,不需要事先指定簇的数量,同时可以形成层次结构,方便分析和可视化。缺点是计算复杂度较高,尤其是对于大规模数据集,同时对初始簇的选取较为敏感,容易陷入局部最优解。
举一个例子
| 商铺编号 |
经度 |
纬度 |
商铺类型 |
营业额(万元) |
| 1 |
116.397128 |
39.916527 |
餐饮 |
120 |
| 2 |
116.397458 |
39.917285 |
餐饮 |
80 |
| 3 |
116.396966 |
39.918009 |
服装 |
200 |
| 4 |
116.397562 |
39.918444 |
服装 |
150 |
| 5 |
116.397982 |
39.917799 |
书店 |
90 |
d(i,j)=(xi−xj)2+(yi−yj)2+w1(ti−tj)2+w2(pi−pj)2
其中,xi和yi表示商铺i的经度和纬度,ti和pi表示商铺i的类型和营业额,w1和w2表示类型和营业额的权重。
伪代码
输入:n个样本的相似度矩阵D,停止合并条件stop
输出:聚类树T
初始化n个初始簇C1,C2,...,Cn
for i = 1 to n do
T.add_node(Ci)
while T 中簇的数量>1 do
找到距离最近的两个簇Ci,Cj
新建一个簇Ck,将Ci,Cj并入Ck
计算新簇与其他簇的相似度,并更新相似度矩阵D
T.add_edge(Ci,Ck)
T.add_edge(Cj,Ck)
删除相似度矩阵D中Ci,Cj两行两列的元素
将Ck与其他簇的相似度加入相似度矩阵D的末尾
if 距离最近的两个簇的距离 > stop then
break
返回聚类树T
这里也说明一个问题就是分层聚类最后输出是一个树状的结构。
高斯混合模型聚类
高斯混合模型聚类(Gaussian Mixture Model Clustering,简称高斯聚类)是一种基于概率密度函数的聚类算法,它假设数据样本是由多个高斯分布混合而成,通过对每个高斯分布的参数进行估计,可以对数据进行聚类。
高斯混合模型聚类步骤
- 初始化模型参数:随机初始化每个高斯分布的均值、方差和权重系数。
- 计算样本属于每个高斯分布的概率:对每个样本计算其属于每个高斯分布的概率,并根据加权平均值确定其所属的簇。
- 更新模型参数:根据当前样本的簇分配情况,重新估计每个高斯分布的均值、方差和权重系数。
- 重复步骤2和3,直到收敛或达到预设的迭代次数为止。
再白话一点,先假设几个簇的均值和方差,这样就构建了几个高斯分布,然后遍历节点,看节点属于哪个分布的概率最大,然后加入到这个簇中,更新分布,依次类推最终构建好一个完整的簇。
高斯聚类的特点
优点
- 可以适用于不同的数据分布,对数据的分布没有假设限制。
- 可以对每个高斯分布的参数进行估计,反映了不同高斯分布在总体数据分布中的贡献程度。
- 可以估计每个样本属于每个高斯分布的概率,得到更加细致的聚类结果。
- 可以通过增加高斯分布的数量来适应更加复杂的数据分布。
缺点
- 对于数据量较大的情况,计算复杂度较高。
- 对初始参数的选取比较敏感,容易陷入局部最优解。
- 对于数据中存在噪声或异常值的情况,容易对聚类结果产生影响。
- 算法的理论基础较为复杂,不易理解和解释。
谱聚类
谱聚类(Spectral Clustering)是一种基于图论的聚类算法,它将数据样本看作是图上的节点,通过对图的特征向量分解来实现聚类。
谱聚类的步骤
- 距离矩阵计算:根据数据样本之间的相似度计算距离矩阵。
- 相似度矩阵计算:根据距离矩阵计算相似度矩阵,常用的相似度计算方法有高斯核函数和K近邻法。
- 拉普拉斯矩阵计算:根据相似度矩阵计算拉普拉斯矩阵,常用的拉普 拉斯矩阵计算方法有对称归一化拉普拉斯矩阵和非对称归一化拉普拉斯矩阵。
- 特征向量分解:对拉普拉斯矩阵进行特征向量分解,得到每个样本点对应的特征向量。
- K-Means聚类:将特征向量作为输入进行K-Means聚类,得到最终的聚类结果。
谱聚类的特点
谱聚类的优点是可以处理非线性可分数据、适用于各种数据分布,且具有较好的聚类效果。同时,谱聚类的计算复杂度与样本数量和特征维度相关,不受样本分布的影响,因此对于大规模数据集具有较好的可扩展性。缺点是需要手动设置参数(如相似度计算方法、K值等),且对于数据中存在噪声或异常值的情况需要进行额外的处理。
谱聚类之所以能解决非线性问题是经过一次矩阵分解,相当于进行了特征的升维提取。
总而言之
K-Means聚类算法
适用场景:适用于大规模数据集,数据分布比较明显的情况,如对用户行为进行分析、对产品分类等。
层次聚类算法
适用场景:适用于数据之间的距离或相似度比较容易计算的情况,如对文本进行分类、对图像进行分割、对基因序列进行聚类等。
DBSCAN聚类算法
适用场景:适用于数据分布比较稠密的情况,可以处理各种形状的聚类簇,对噪声和异常值具有较好的鲁棒性,如对地理位置进行聚类、对网络攻击进行检测等。
高斯混合模型聚类算法
适用场景:适用于数据分布不同或者数据分布未知的情况,可以估计每个样本属于每个高斯分布的概率,得到更加细致的聚类结果,如对客户进行分类、对金融市场进行分析等。
谱聚类算法
适用场景:适用于非线性可分数据,对数据分布没有假设限制,具有较好的聚类效果,对大规模数据集有较好的可扩展性,如图像分割、社交网络分析、生物信息学等领域。