时间序列预测(五)--Prophet模型

今天来介绍一个Prophet模型是FB出品的一个可解释性极强的一个模型，使用起来十分简单，咱们主要还是讲解其中的原理。

Prophet模型

Prophet模型使用经典的时间分解预测的方法，将预测任务分类趋势影响、季节影响、节假日影响，以及噪声影响，这也比较适合咱们的时间预测的场景。

y_{t}=g(t)+s(t)+h(t) \tag{1.1}

$y_{t}$ 是预测值， $s(t)$ 季节趋势、 $g(t)$ 趋势函数， $h(t)$ 节假日影响。当然上文使用的加法模型，也可以使用其他模型。

这里需要普及一下时间分解的方法，你可能会觉得这直接拆成了3份，如何做模型呢？其实趋势项一般是预测一段时间内的均值，刻画整个序列的趋势的。这里文中使用了两种方法，一种是逻辑回归，一种是分段线性回归。

图1-1

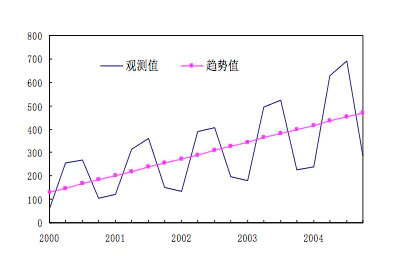
逻辑回归的一形式如下

\sigma(x)=\frac{1}{1+e^{-x}} \tag{2.1}

然后他有一个特别舒服的导数形式。本文使用是的如下的形式。

f(x)=\frac{C}{1+e^{-k(x-m)}} \tag{2.2}

其中C是承载量，就是是如果你是统计UV，那么你这些UV是由多少个用户产生的？就是这个C。k表示增长率，m表示曲线中点，现实中C、k、m不是一成不变的值而是一个函数，g(t)的最终形式如下。

g(t)=\frac{C(t)}{1+exp(-(k+a(t)\delta))*(t-(m+a(t)r))}

其中，a(t)表示序列中的变点参数，t表示时间戳,当有变点的时候是1，没有变点是0，$$\delta$$表示每个变点以后增长率变化.r是边界处理。

g(t)=(k+a(t)\delta)t+(m+a(t)r)

目标涵数如上， k是增长率， $\delta$ 是增长率变化率，m是离线参数。

季节性符合傅里叶变化趋势。

s(t)=\sum_{1}^{N}(a_{n} cos(\frac{2 \pi nt}{P})+b_{n}sin(\frac{2 \pi nt}{P}))

P表示周期，P=7表示周为周期，当N=3的时候。

X(t)=[cos(\frac{2 \pi (1)t}{7}),...,sin(\frac{2 \pi (3)t}{7})]

s(t)=X(t)\beta

$\beta = Normal(0, \sigma^{2})$

h(t)=Z(t)k \\ k=Normal(0, v^{2})

v受默认的节假日的超参影响。

最后使用这个多维度的分量进行累加以后就完成了这个预测值的预测，因为算法本身使用了大量分布数据，所以预测值也能预测数数据分布。大家可以在使用过程中体会。