思考如下问题，如果有一个数据集合不是特别容易分类，这个可能是我们的数据维度并不能描述我们的数据本身，导致我们不能将数据完全切分开，如果能经过相应的变换，让我们的数据在某个变换以后变得显而易见，那是不是我们就解决了分类问题呢？本文就将介绍这这样的一个算法。就如下图所示。

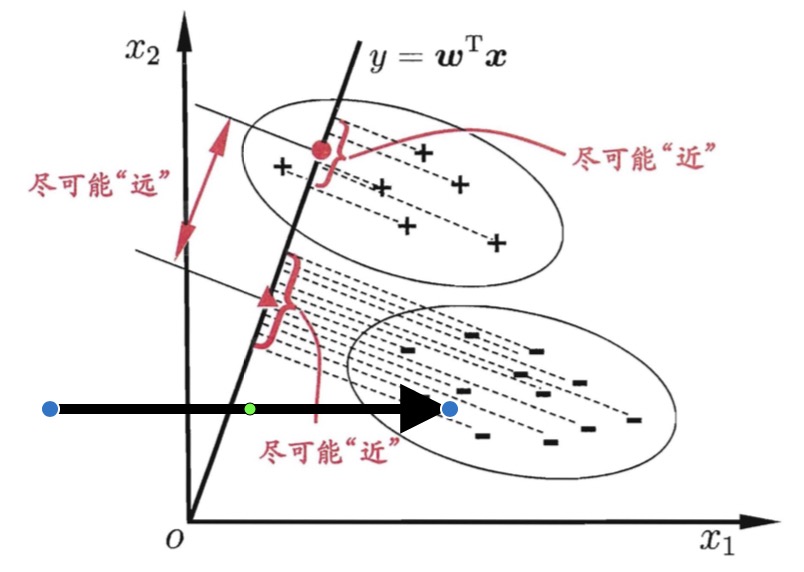
LDA算法描述

现在我们用白话了解了一个问题，接下来我们需要用数学的语言将这个问题定义出来。这里想要提醒大家，学习一个问题，对于算法的同学，比较重要的是将这个问题的数学表达定义好，否则问题会变得格外的复杂和无从下手。大的思路还是要将原始数据x,通过权重矩阵w，转变成y且也具有比x更好的区分的性能。

$$y=wx$$

对于这个问题的输入数据是这样的,我们有$n$个样本数据，它们的特征向量是$x_i$,属于不同的类别。其中属于类$C_1$的样本集合为$D_1$,且有$n_1$个样本，属于$C2$的样本集合$D_2$有$n_2$个。对于每类样本的均值的定义为

$$\vec{m}=\frac{1}{n}\sum_{x \in D_i}x$$

经过投影后的均值为

$$m=\frac{1}{n}\sum_{x \in D_i}w^Tx$$

投影后两类样本的均值绝对差为：

$$w^T(m_1-m_2)$$

而对于类内的误差，我们使用方差来衡量，i表示第i类。

$$s_{i}^{2}= \sum (y-m_i)^2$$

这时候我们想要的损失函数是怎样的呢？我们肯定希望投影以后的数据，类内间距尽量小，类间的间距尽量大，所以不难定义我们的损失函数。

$$L(w)=\frac{(m_1-m_2)^2}{s_{1}^{2}+s_{2}^{2}}$$

我们发现这个损失函数竟然连w都没有，我们必需想尽办法写成关于w的函数，至于为什么呢？我们想求梯度，当然需要有优化的对象呀。

定义类内的散布函数如下

$$S_i=\sum (x-m_i)(x-m_i)^T$$

总体的散布矩阵为

$$S_w=S_1 + S_2$$

这样就有

$$s_{i}^{2}=\sum (w^T-w^Tm)^2$$

$$=\sum w^T (x-m_i)(x-m_i)^T w$$

$$=w^TS_iw$$

这样总体的个个类的散布之和为

$$s^{2}_1+ s^{2}_2=w^TS_ww$$

好了，从这里开始我们已经结束了分母的改写，接下来咱们就开始处理分子。

$$(m_1-m_2)^2=(w^T(m_1-m_2))^2=w^T(m_1-m_2)(m_1-m_2)^Tw$$

如果定义$S_B=(m_1-m_2)(m_1-m_2)$,那么

$$(m_1-m_2)^2=w^TS_Bw$$

综合上面的描述，我们的最后的大公式终于出炉拉。

$$L(w)=\frac{w^TS_Ww}{w^TS_Bw}$$

我们尝试加上一个约束条件

$$w^TS_Ww=1$$

这问题又转化到了一个带有限制条件的最优化问题。

$$max\ w^TS_Bw$$

$$st.w^TS_Ww=1$$

$$L=w^TS_Ww + \lambda(w^TS_ww-1)$$

对$w$求导，能够得到

$$S_Bw+\lambda S_ww=0$$

$$S_Bw=\lambda S_ww$$

同时乘以$S_w^{-1}$

$$S_w^{-1}S_Bw=\lambda w$$

发现了什么？

$\lambda$是$S_w^{-1}S_Bw$的特征值，$w$是特征向量，将这个表达式放到目标函数中。

$$\frac{w^TS_Ww}{w^TS_Bw}=\frac{w^T(\lambda S_Ww)}{w^TS_ww}=\lambda$$

所以最大特征值
和其对应的特征向量就是本问题的最优解。

那么最后的问题来了，即使投射到一维空间，如何做分类呢？ 其实我们可以把这个问题想简单点，例如KNN算法的方式也是可以接受的，就是用它的邻居来决定它的分类。