xgboost

xgboost可能是现在用的最多的模型了，炒的火热的深度学习解决实际业务的落地点还是比较少的，比起这种可解释模型，在工程界可能更加受追捧。

xgboost的组成

话说xgboost是由什么组成的呢？答案就是一堆CART树，但是有了这些CART树怎么做预测呢，难倒是投票，好吧也是一种方式，但是如果多个CART树都采用同样的样本数据，那可能结果也是惊人的一致，大家都会为你转身？ 其实xgboost使用的方式是多个CART树的预测结果进行加权相加，最后就是预测结果。

我们尽量用官网的例子进行说明

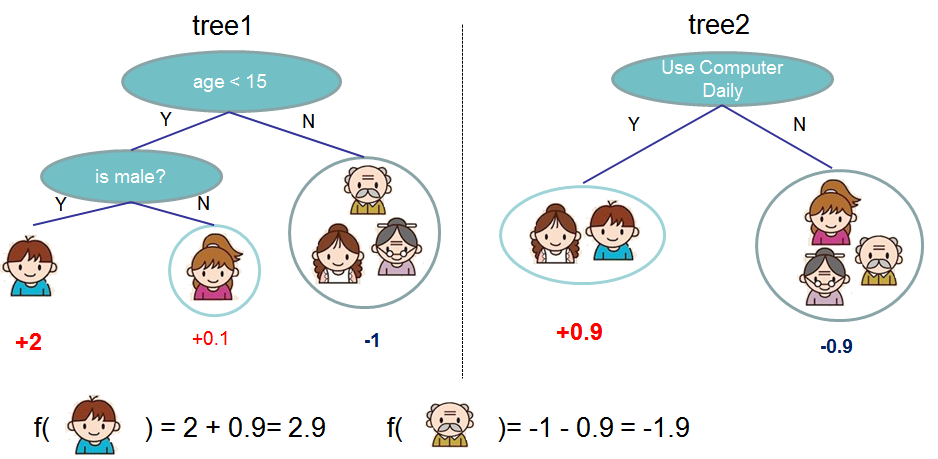
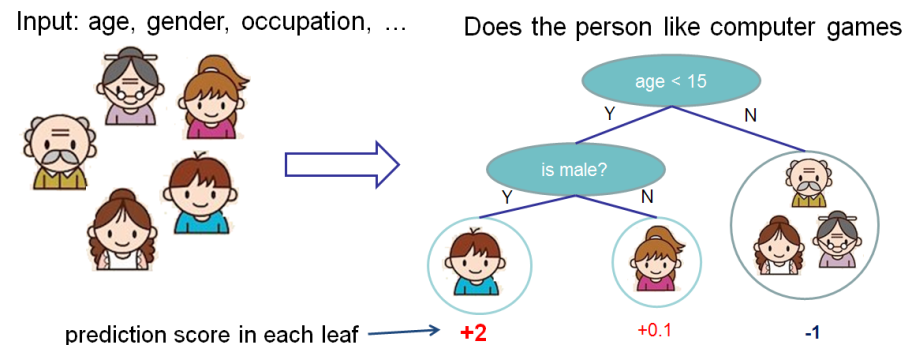
第二图的底部说明了如何用一堆CART树做预测，就是简单将各个树的预测分数相加。

xgboost为什么使用CART树而不是用普通的决策树呢？
简单讲，对于分类问题，由于CART树的叶子节点对应的值是一个实际的分数，而非一个确定的类别，这将有利于实现高效的优化算法。xgboost出名的原因一是准，二是快，之所以快，其中就有选用CART树的一份功劳。

xgboost的数学表达

$$y_i=\sum f_k(x_i)$$

这里的K就是树的棵数，f表示所有可能的CART树，f表示一棵具体的CART树。这个模型由K棵CART树组成。模型表示出来后，我们自然而然就想问两个问题

一、这个模型的参数是什么？因为我们知道，“知识”蕴含在参数之中。

二，用来优化这些参数的目标函数又是什么？

咱们来看看目标函数这个问题，以为面对一个学习算法的时候最重要的就是目标函数。

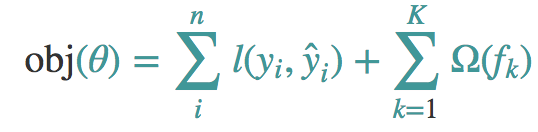
这个目标函数同样包含两部分，第一部分就是损失函数，第二部分就是正则项，这里的正则化项由K棵树的正则化项相加而来，你可能会好奇，一棵树的正则化项是什么？后面会解释这个问题。

xgboost的训练

现在我们总算是知道目标函数了，现在就是让目标函数最小化的过程了。 奇怪的是我们没有找到参数呀，如果是个线性回归我们还可以知道参数在表达式里，但是CART树需要什么参数呢。瞬间懵逼了。

根据我们对CART树的理解，确定一棵CART树需要确定两部分，第一部分就是树的结构，这个结构负责将一个样本映射到一个确定的叶子节点上，其本质上就是一个函数。第二部分就是各个叶子节点上的分数。

你要说叶子节点的分数作为参数，还是没问题的，但树的结构如何作为参数呢？而且我们还不是一棵树，而是K棵树!

假设一下，如果K棵树的结构都已经确定，那么整个模型剩下的就是所有K棵树的叶子节点的值，模型的正则化项也可以设为各个叶子节点的值的平方和。此时，整个目标函数其实就是一个K棵树的所有叶子节点的值的函数，我们就可以使用梯度下降或者随机梯度下降来优化目标函数。现在这个办法不灵了，必须另外寻找办法。

加法训练

所谓加法训练，本质上是一个元算法，适用于所有的加法模型，它是一种启发式算法。运用加法训练，我们的目标不再是直接优化整个目标函数，这已经被我们证明是行不通的。而是分步骤优化目标函数，首先优化第一棵树，完了之后再优化第二棵树，直至优化完K棵树。整个过程如下图所示：

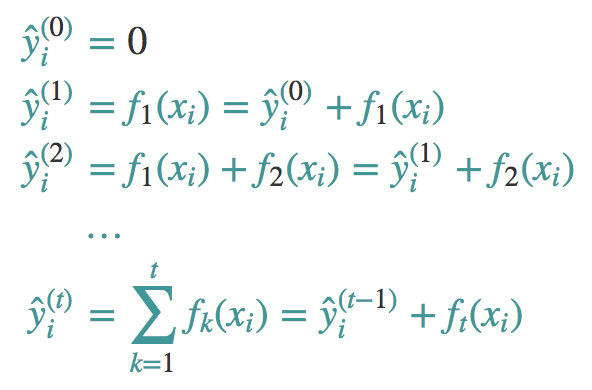
到达第t步的时候，我们添加一颗最优的CART树$f_t$,这棵最优的CART树$f_t$是怎么得来的呢？非常简单，就是在现有的t-1棵树的基础上，使得目标函数最小的那棵CART树，如下图所示：

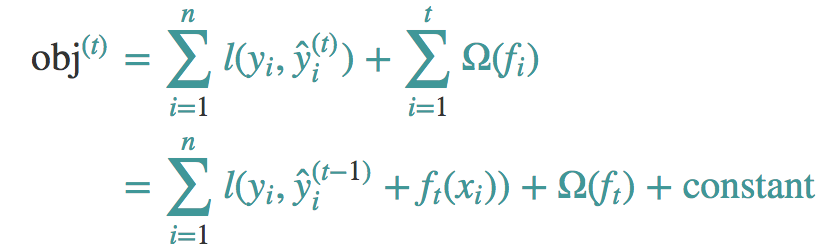
如果我们采用MSE当做我们的损失函数。

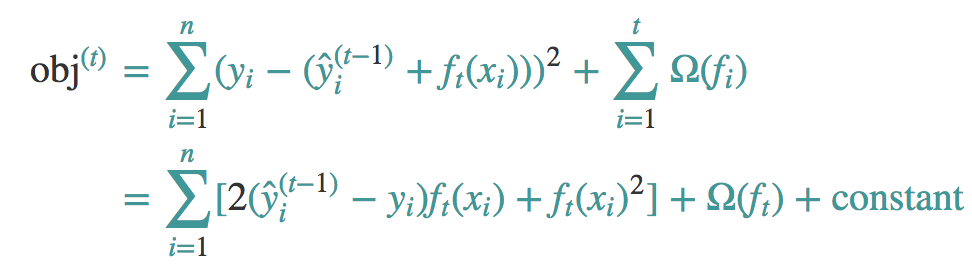
可以看到MSE是很好的，它是包含$f_t$的一次式子和二次式子，而且一次式项的系数是残差。

注意：$f_t(x_i)$是什么？它其实就是$f_t$的某个叶子节点的值。之前我们提到过，叶子节点的值是可以作为模型的参数的。

这里我们使用泰勒展开式来近似原来的表达式。

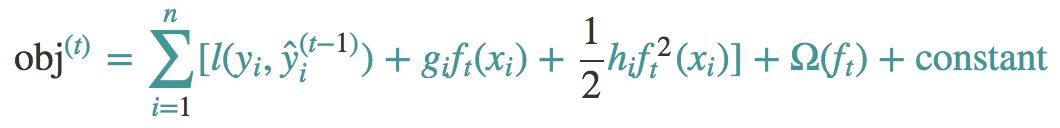
这里的h和g就是下面的表达

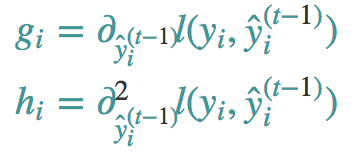
这里我们还是要说一下，g和h实际上就是损失函数的一阶导数和二阶导数。这里就是为什么我们可以指定自己的损失函数，只要损失函数可以有二阶导数就可以拿来当我们的损失函数。

举个栗子：
假设我们正在优化第11棵CART树，也就是说前10棵 CART树已经确定了。这10棵树对样本$(x_i,y_i=1)$的预测值是$y^i=-1$，假设我们现在是做分类，我们的损失函数是交叉熵.

$$L=\sum y^i ln(1+e^{-y^i}) + (1-y^i)ln(1+e^{y^i})$$

当$y_i=1$的时候，损失函数就变成了

$$L=ln(1+e^{-y^i})$$

而它的导数就是

$$\frac{-e^y}{1+e^y}$$

将$y=-1$带入，就得到了-0.27=g，这个值是负的，也就是说，如果我们想要减小这10棵树在该样本点上的预测损失，我们应该沿着梯度的反方向去走，也就是要增大$y^i$ 的值,使其趋向于正，因为我们的$y_i=1$就是正的。你也许会说，这肯定要计算很多个g和h，对的 你说的很对，但是想想这些g和h的计算是独立的，无非就是并行计算就能解决这些计算量，所以对我们来说也是好事。

当我们消灭所有的常数的时候就有了如下的表达式:

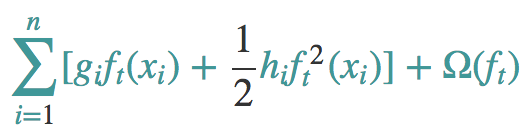
模型复杂度

其实我们还有一个问题没有解决，那就是正则化项去哪里了，这个其实是我们之前回避的一个问题，那么现在我们来好好说说。让我们来重新定义$f(x)$，

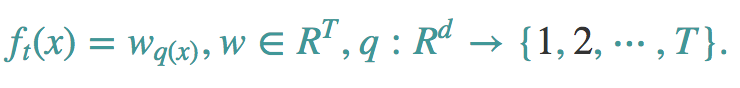
一棵树有T个叶子节点，这T个叶子节点的值组成了一个T维向量w，q(x)是一个映射，用来将样本映射成1到T的某个值，也就是把它分到某个叶子节点，q(x)其实就代表了CART树的结构。$w_q(x)$自然就是这棵树对样本x的预测值了。

那么我们使用下面这个正则化项。

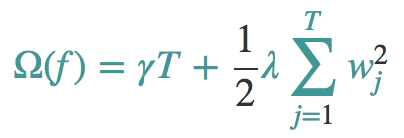
注意：这里出现了γ和λ，这是xgboost自己定义的，在使用xgboost时，你可以设定它们的值，显然，γ越大，表示越希望获得结构简单的树，因为此时对较多叶子节点的树的惩罚越大。λ越大也是越希望获得结构简单的树。

当然之所以这么定义，完全是经验的结果。

接近尾声

现在我们来看看第t课树的优化目标：

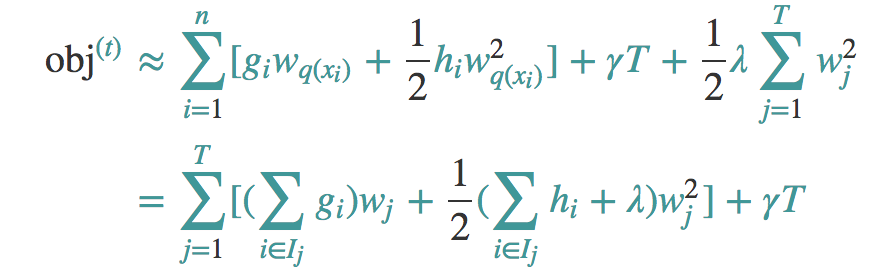
$I_j$它代表一个集合，集合中每个值代表一个训练样本的序号，整个集合就是被第t棵CART树分到了第j个叶子节点上的训练样本。

当然上面的公式是可以被简化为如下形式:

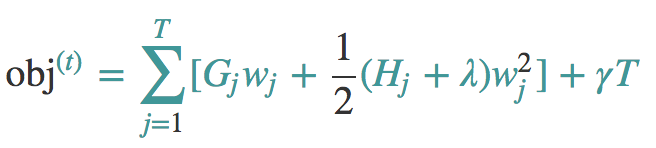
对于第t棵CART树的某一个确定的结构（可用q(x)表示），所有的$G_j$和$H_j$都是确定的。而且上式中各个叶子节点的值$w_j$之间是互相独立的。上式其实就是一个简单的二次式，我们很容易求出各个叶子节点的最佳值以及此时目标函数的值。如下所示：

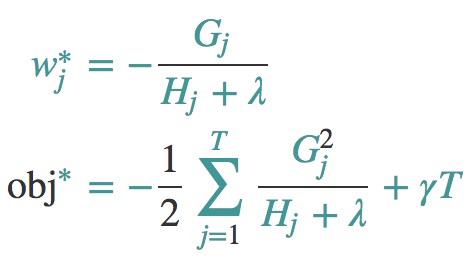
第一个公式是对obj进行$w_j$求导为0，第二个式子就是将w带入就可以。

obj表示了这棵树的结构有多好，值越小，代表这样结构越好！也就是说，它是衡量第t棵CART树的结构好坏的标准。这个值仅仅是用来衡量结构的好坏的，与叶子节点的值可是无关的。为什么？请再仔细看一下obj的推导过程。obj只和$G_j$和$H_j$和T有关，而它们又只和树的结构(q(x))有关，与叶子节点的值可是半毛关系没有。

上面这个图就能计算这个树到底有多好。什么 不懂？ 那就再详细说说。

看看咱们对于$w^*$的解释，加入分到第j个叶子上的节点只有一个对象，那w应该是什么样子。

$$w*=\frac{1}{h_j+\lambda} (-g_j)$$

咱们是不是可以这么看，$\frac{1}{h_j+\lambda}$ 这个就是学习率，而$(-g_j)$很显然是一阶导数也就是梯度的负方向。

这个式子告诉我们，$w_j$的最佳值就是负的梯度乘以一个权重系数，该系数类似于随机梯度下降中的学习率。观察这个权重系数，我们发现，$h_j$越大，这个系数越小，也就是学习率越小。$h_j$越大代表什么意思呢？代表在该点附近梯度变化非常剧烈，可能只要一点点的改变，梯度就从10000变到了1，所以，此时，我们在使用反向梯度更新时步子就要小而又小，也就是权重系数要更小。

真的要结束了

有了评判树的结构好坏的标准，我们就可以先求最佳的树结构，这个定出来后，最佳的叶子结点的值实际上在上面已经求出来了。

问题是：树的结构近乎无限多，一个一个去测算它们的好坏程度，然后再取最好的显然是不现实的。所以，我们仍然需要采取一点策略，这就是逐步学习出最佳的树结构。这与我们将K棵树的模型分解成一棵一棵树来学习是一个道理，只不过从一棵一棵树变成了一层一层节点而已。如果此时你还是有点蒙，没关系，下面我们就来看一下具体的学习过程。

我们就用官网的例子来解释这个事情。

最简单的树结构就是一个节点的树。我们可以算出这棵单节点的树的好坏程度obj*。假设我们现在想按照年龄将这棵单节点树进行分叉，我们需要知道：
1、按照年龄分是否有效，也就是是否减少了obj的值
2、如果可分，那么以哪个年龄值来分。

为了回答上面两个问题，我们可以将这一家五口人按照年龄做个排序。如下图所示：

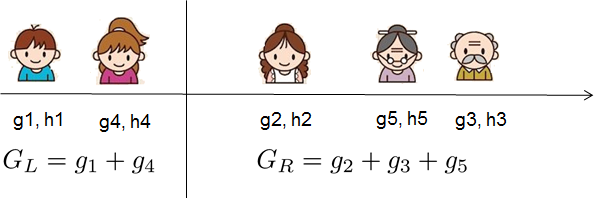
按照这个图从左至右扫描，我们就可以找出所有的切分点。对每一个确定的切分点，我们衡量切分好坏的标准如下：

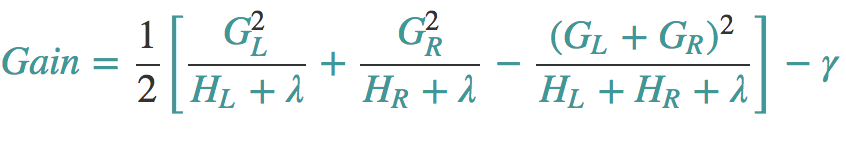
这个Gain实际上就是单节点的obj减去切分后的两个节点的树obj，Gain如果是正的，并且值越大，表示切分后obj越小于单节点的obj，就越值得切分。同时，我们还可以观察到，Gain的左半部分如果小于右侧的γ，则Gain就是负的，表明切分后obj反而变大了。γ在这里实际上是一个临界值，它的值越大，表示我们对切分后obj下降幅度要求越严。这个值也是可以在xgboost中设定的。

扫描结束后，我们就可以确定是否切分，如果切分，对切分出来的两个节点，递归地调用这个切分过程，我们就能获得一个相对较好的树结构。

注意：xgboost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度，而依赖后续的剪枝操作来控制。xgboost在切分的时候就已经考虑了树的复杂度，就是那个γ参数。所以，它不需要进行单独的剪枝操作