支持向量机
支持向量机,千呼万唤始出来,SVM作为远古时期最接近深度学习的算法,理论想起来比较简单,但是想要理解深刻还是需要花些周章的,这里会尽我所能给出一个比较好解释的方式。
SVM应该是第一个解决线性不可分的算法,假如我没有孤陋寡闻的话,这里会介绍基本的SVM原理,高维度经过核函数转换的会提到,但是不会深入讲,因为原理都是一样的。
起点
好吧,尴尬的是复杂的问题总是从简单的问题演变过来的,这个其实对于一个学习者来说是痛苦的,你想要了解A,就会发现你必须要了解B。。。,所以我们会一直强调基础基础。
线性回归记得吗?
wT+b=0
好熟悉的表达式,其中w=(w1,w2,,,,wn)是n个参数。
这是一个二维空间中,我们用一条线切分两个类别显得十分简单,思考这个问题,对于样本空间而言,是否存在一个超平面空间,我们需要找到一个面切分两个类别。盗个图解释一下。
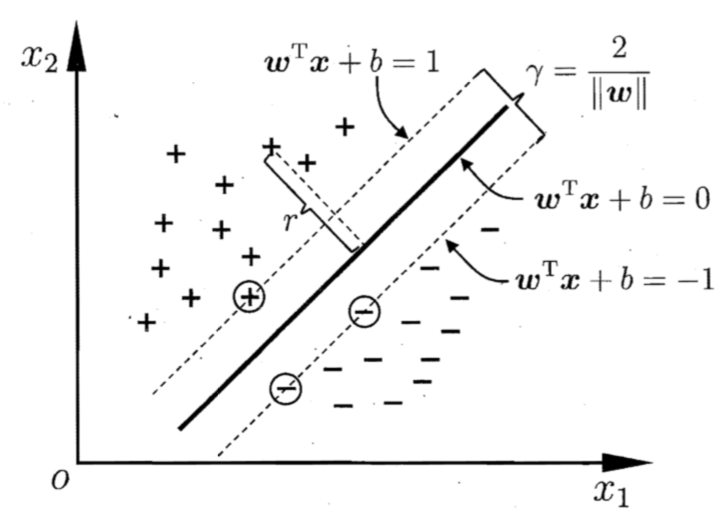
r=∣∣w∣∣wT+b
且满足
wTxi+b>=1 yi=1
wTxi+b<=1 yi=−1
在向量空间中,两条直线的间隔可以表示为
r=∣∣w∣∣2
我们要找到一个很好的间隔,我们就要满足如下表达式
max∣∣w∣∣2
st. y(wTxi+b)>=1
好了,支持向量机的内容讲完了! 是不是很突然,核心的思想就没有了。
对偶问题
上面一节中咱们给出我们要满足的条件,但是怎么求呢?原来在拉格朗日乘子中讲过这类问题的优化方法,这个就是基础基础。咱们就试着用这样的方法求的上一节提到的条件下w的值。
第一步添加拉格朗日乘子。
L(w,b,α)=21∣∣w∣∣2+∑α(1−yi(wTxi+b))
第二步,对要求的参数求偏导且等于0
w=∑αiyixi
0=∑αiyi
接下来的步骤就简单了。将偏导等于0的式子w带入L(w,b,α)
L(w,b,α)=21∑αiαjyiyjxTx+∑αi−∑αiyiαjyjxjxi−∑αibyi
L(w,b,α)=max∑α−21∑∑αiαjyiyjxixj
st.0=∑αiyi
推导到上面这个过程,也就差不多了,当然咱们这个问题需要满足KKT条件,这个在拉格朗日乘子中也是讲过的。
为了计算上面这个式子,一般会使用SMO算法,大致的思想就是先固定α以外的所有产出,然后调节α。
最终我们会的到一个支持向量,模型最后只需要保存这个支持向量。
核函数
咱们将支持向量机讲到这里貌似已经结束了,但是我们还有一个问题就是,这一些的假设都是线性可分的情况下,如果遇到线性不可分的情况下,该如何找到一个线或是面来切分样本呢?这个时候我们就引入和核函数。
这里我来重新看一下原始的公式
f(x)=wT∅(x)+b
看起来很好理解,我们将输入样本x,在有限维度的空间下,进行一次核函数映射,这个核函数的选取有很多种,可以自行查阅一下,∅(x)就是我们说的核函数。
这里不去展开讲,当然这里同样很复杂,但是原理上应该通的,所以没有必须讲的太仔细。