基于策略的深度强化学习

循环确定性策略梯度(RDPG)

RDPG属于策略梯度算法。和前面讲到的基于值函数的训练方法不同，策略通过计算梯度更新策略网络中的参数，使得整个策略朝着奖励增高的方向更新。

基于DQN的方法动作都是离散的，但是实际的应用中动作空间往往是连续的，例如自动驾驶的方向盘转换角度等。主要原因还是因为DQN的学习方式是随机策略进行探索，但是对于一个连续或者是高维度的问题，就会出现模型很难收敛以及需要探索的的空间过于巨大。

这就引出了另一种策略的更新方法，策略梯度方法，也就是本章的主题确定策略梯度方法（DPG）。

POMDP（部分可观察MDP）

这里也介绍一个新的强化学习场景，POMDP，主要是针对一些场景中不能观察到完整的上下文信息，例如自动驾驶场景，我们利用驾驶员的操作记录来作为强化学习的数据，但是驾驶员观察的信息可能是远远高于车上的摄像头以及雷达的。例如驾驶员看到了远处有人准备开始过道，但是摄像头可能还没有采集到，这个时候数据呈现的样式就是踩了刹车，这样就会对学习到这个过程会产生巨大的困难 。

RDPG算法介绍

RDPG使用RNN神经网络来构造估计策略的确定策略梯度算法。这种算法在POMDP的场景尤其试用，这是因为每个智能体只能观察环境中的一部分，环境的真实状态是无法得到的。所以为了逼近真实状态，我们用从开始到现在的观察片段来逼近整个环境。而RNN的使用，使得我们不需要每次从头开始观察所有片段，而是存储在RNN的隐状态中，每次这增加当前观察片段即可。

RDPG算法过程

作为actor-critic算法族中的一员，RDPG中也使用了策略网络和价值网络。价值网络用于估计状态-动作价值，然后把评分信息送到策略网络中，用作动作函数在Q网络上的几何梯度$\Delta_{a}Q^{critic}(o,a)$.。
更新的过程是首先扫描代表过去一段时间的状态向量$h_{-1}$

$$h_{-1}=f((o_{t})|h_{init}) \tag{1.1}$$

其中t代表观察到的时间长度，，f是策略网络或者价值网络中记忆过去一段时间的RNN函数。

之后， 计算从经验池中选取的小批量的TD梯度数据，也就是预测价值网络的误差梯度$\Delta_{\theta}L(\theta^{Q})$

$$\Delta_{\theta}L(\theta^{Q})=\frac{1}{NT} \sum_{i}\sum_{t}(Q(h_{t,i},a_{t,i}|\theta^{Q})-y_{t}^{i})\Delta_{\theta}Q(h_{t,i},a_{t,i}|\theta^{Q}) \tag{1.2}$$

其中$y_{i}^{i}$是通过价值网络计算出来的预期目标值。目标价值网络的输入是下一个时刻的历史状态$h_{i+1}^{i}$和下一个时刻状态下的动作$a_{t+1,i}$,该动作是由目标策略网络µ’产生的，其输入是$h_{i+1}^{i}$，$y_{t}^{i}$的计算过程是

$$y_{t}^{i}=\gamma^{i}_{t}+\gamma Q'(h_{i+1}^{i},µ'(h_{i+1}^{i}|\theta^{µ'})|\theta^{Q'}) \tag{1.4}$$

然后使用ADAM优化器通过最小化上述价值网络的误差来更新价值网络。然后我们使用Q网络梯度来计算策略网络的梯度

$$\Delta _{\theta^{µ}}J=\frac{1}{NT} \sum_{i}\sum_{t} \Delta _{a} Q(h,a|\theta^{Q}) \Delta_{\theta^{µ}} µ(h|\theta^{µ}) \tag{1.5}$$

在循环使用确定性神经网络中，还使用了经验复用的优化训练过程。这是这个复用会有一点不同是每次采用一个片段进行训练。

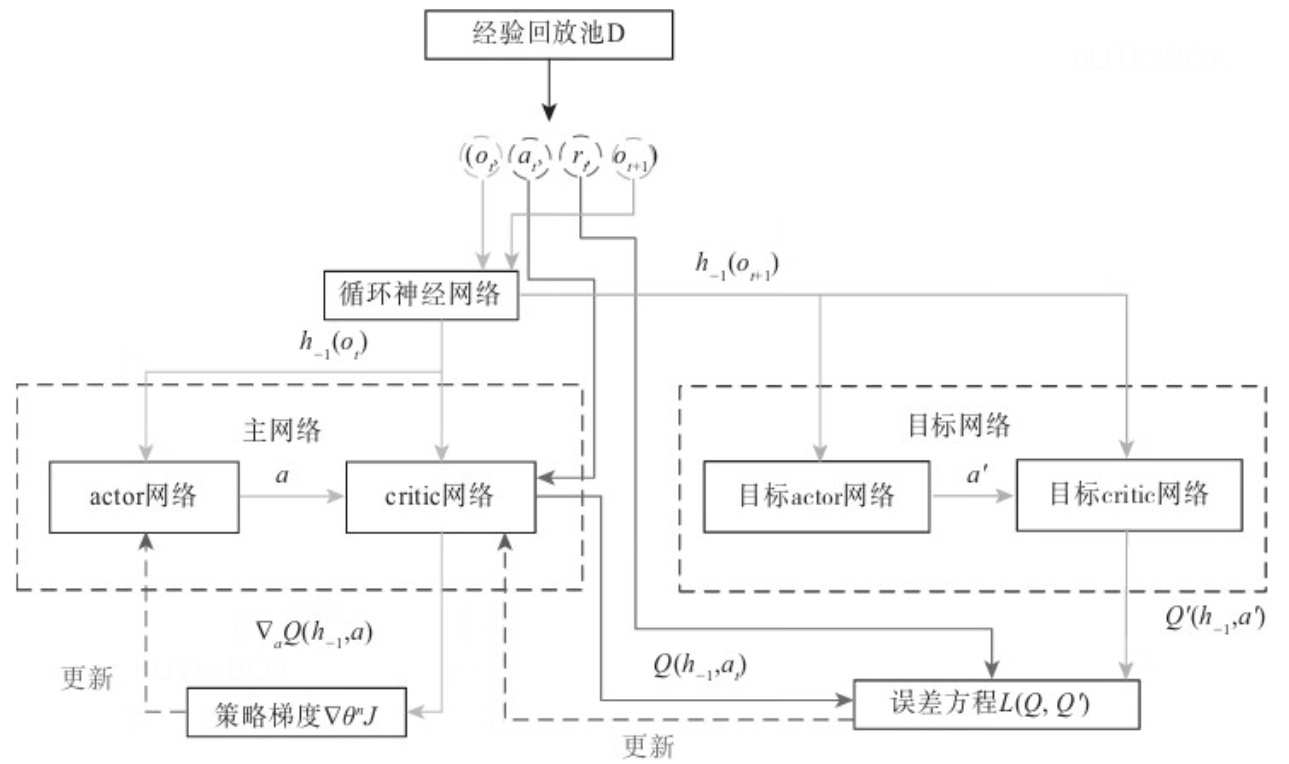
伪代码

使用场景

RDPG从提出来以后主要是解决智能体在POMDP的环境中无法得到全局的状态的情况下怎么根据当前的观察以及之前的记忆经验得到一个近似的最优策略。