今天来介绍经典算法中的回溯算法，这类算法是一种弱枚举（这里大家千万不要认为枚举很low，很多问题能够枚举出来还是万幸的）的算法，一般如果代码实现十分简单，但是真的思考出来还是有些难度的，因为一般使用递归实现，所以代码十分简洁，但是执行过程会让你十分痛苦，你即使在项目中打上断点追踪，最后很快就追丢了。所以本节咱们来列举几个经典问题，然后详细介绍一下这类问题的解决办法。

组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。 
例如， 
输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
] 

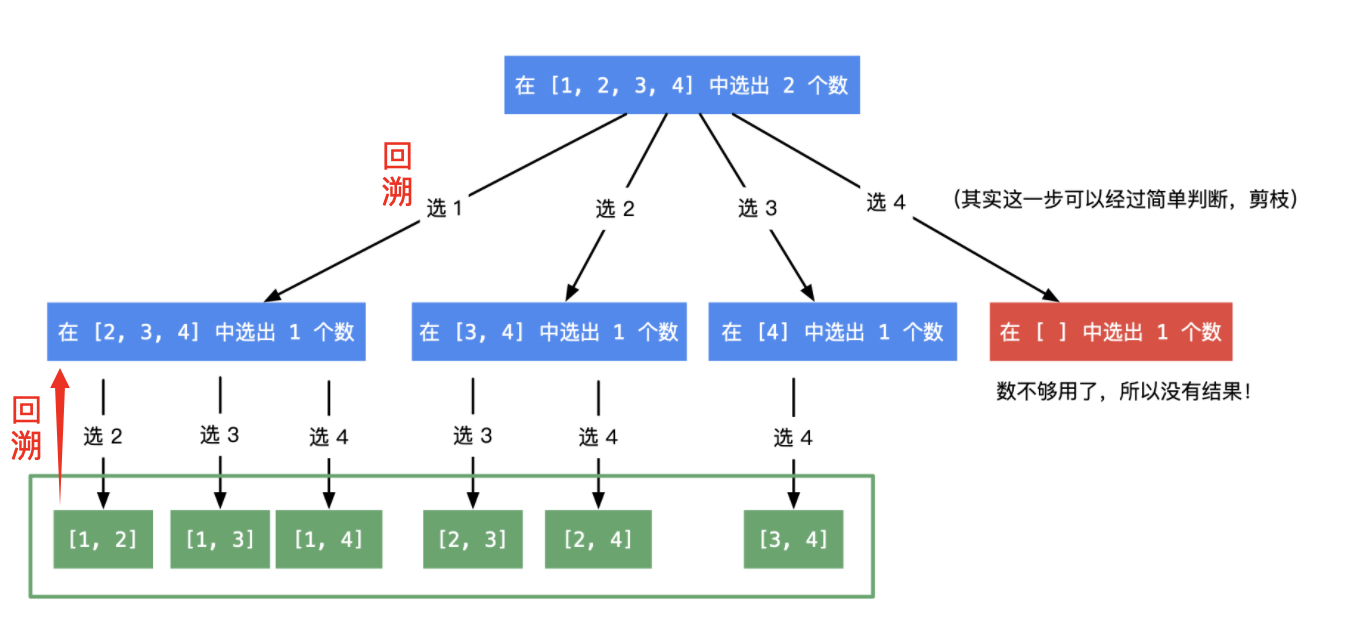
我们来看上面的这个图，所谓的回溯策略，就是我完成了当前的一个节点的枚举以后，要回退到上一个节点重新进行枚举。结合上面这个图来看看下面的代码。

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        res = list()
        if k == 0 and n < k:
            return res
        path = list()
        self.dfs(n, k, 1, path, res)
        return res

    def dfs(self, n, k, begin, path, res):
        if len(path) == k:
            res.append(path[:])
            return
        for i in range(begin, n+1, 1):
            path.append(i)
            self.dfs(n, k, i+1, path, res)
            path.pop()

关键函数dfs, 这个一个递归的算法，所以一定要弄一个递归的出口，很显然，这个dfs就是为了枚举所有可能的组合，退出条件就是当path长度等于目标的长度就退出就可以啦。然后我们来看19行的for循环。如上图的根节点，第一位要枚举所有的可能节点，然后放到path中暂存，然后到达第二层树节点，这里因为使用了其中一个数字开头，所以只能选择后面的数字进行组合，所以递归调用i+1,不断放到path中，符合条件就退出保存到res中，最后22行的时候有一个pop操作，它的目的就是图中的回溯操作，每枚举一个，要将尾部回退回去，然后重新枚举其他的组合。

全排列

这意思一道经典的问题，题目如下描述。

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列
输入
nums = [1,2,3]
输出
[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

遇到这样的问题，首先还是画回溯树，确定回溯路径。

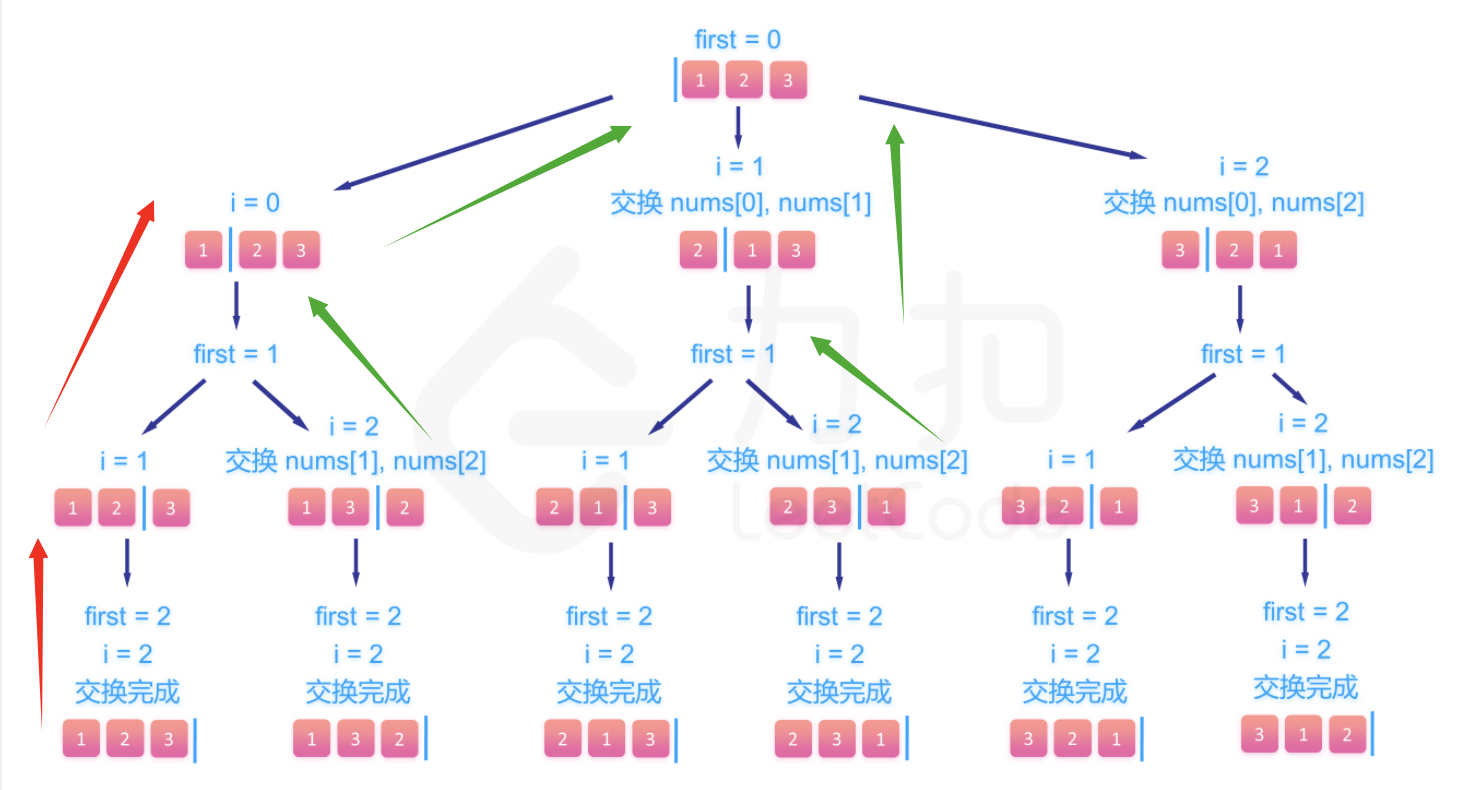
看上面的图，根节点是空，起始的位置是空，然后第一位可以是1/2/3.从1的节点往下枚举，第二层有两个选择[2,3],[3,2],这里是通过交换获得的，当选择好第一位的时候，后面所有的交换方案就是后面的枚举方案，同理固定好依次几位，通过交换的方式获取不同的方案。

class Solution(object):
    @debugHelper
    def permution(self, nums, pos, N):
        if pos == N:
            sa.append(nums[:])
        else:
            for i in range(pos, N):
                nums[i], nums[pos] = nums[pos], nums[i]
                self.permution(nums, pos + 1, N)
                nums[pos], nums[i] = nums[i], nums[pos]
        return sa

    def permute(self, nums):
        global sa
        sa = list()
        self.permution(nums, 0, len(nums))
        return sa

这里类似的结构是8到10行，类似绿色箭头的操作就是，除了要枚举交换的结果，还要还原到父节点上。以备尽行新的回溯操作。否则回溯将漏解，许多重复的结果出现在解里，但是真正的解却没有出现。

单词搜索

接下来，我们看一个比较难的题目，单词搜索。

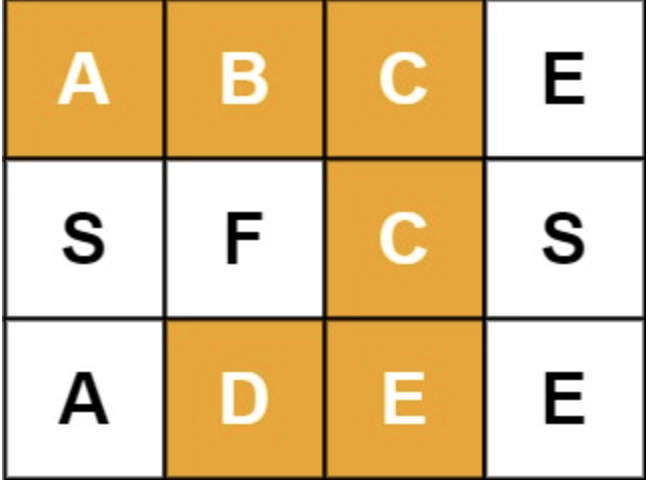
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

class Solution(object):
    def exist(self, board, word):
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        h, w = len(board), len(board[0])
        def check(i, j, k):
            if board[i][j] != word[k]:
                return False
            if k == len(word) - 1:
                return True
            visited.add((i, j))
            result = False
            for ix, jx in directions:
                new_i, new_j = i + ix, j + jx
                if 0 <= new_i < h and 0 <= new_j < w:
                    if (new_i, new_j) not in visited:
                        if check(new_i, new_j, k + 1):
                            result = True
                            break
            visited.remove((i, j))
            return result
        visited = set()
        for i in range(h):
            for j in range(w):
                if check(i, j, 0):
                    return True
        return False

这里第3行是指定回溯回溯方向，对于矩阵来讲就是四个方向，6到9行是递归出口，经典的是第16行，它把每个单词搜索拆成了若干个小的搜索任务，例如有单词“china”，当我们找到字符'c'的时候，就走到的新的位置上，同时搜索的目标变成向四面八方搜索“hina”，搜索方式不变，从而不断的回溯整个搜索过程，代码看起来很多，但是核心思路并不是特别难。

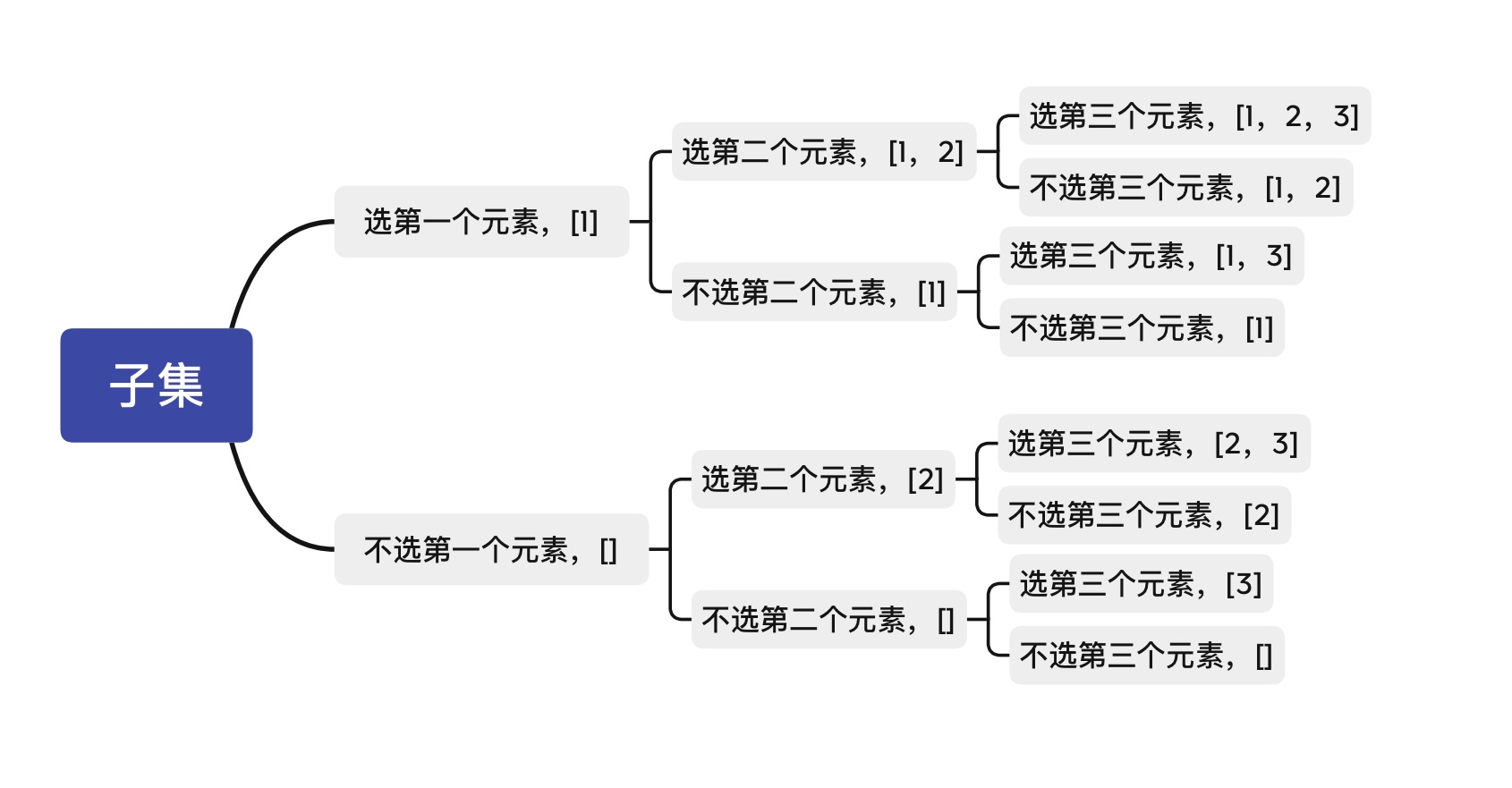
子集

题目描述:  给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集
# 输入：nums = [1,2,3]
# 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

class Solution(object):
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        result = list()
        item = list()
        result.append(item)
        if len(nums) == 1:
            return [[], nums]
        def dfs(i, nums):
            if i >= len(nums):
                return
            item.append(nums[i])
            result.append(item[:])
            dfs(i + 1, nums)
            item.pop()
            dfs(i + 1, nums)
        dfs(0, nums)
        return result
s = Solution()
nums = [1,2,3]
print(s.subsets(nums))