树
本章节主要介绍基于树一些常见的操作和算法。
二叉树
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
二叉树中序遍历
# 递归版本
class Solution(object):
def inorderTraversal(self, root):
if root is None:
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
# 非递归版本
class Solution:
def inorderTraversal(self, root):
# 注意:根节点为空,直接返回空列表
if not root:
return []
stack = []
res = []
while root or stack:
# 一直向左子树走,每一次将当前节点保存到栈中
if root:
stack.append(root)
root = root.left
# 当前节点为空,证明走到了最左边,从栈中弹出节点加入结果数组
# 开始对右子树重复上述过程。
else:
cur = stack.pop()
res.append(cur.val)
root = cur.right
return res
def preorderTraversal(self, root):
if not root:
return []
stack = [root]
res = []
while stack:
# 根节点出栈
node = stack.pop()
# 将根节点值加入结果
res.append(node.val)
# 右子树入栈
if node.right:
stack.append(node.right)
# 左子树入栈
if node.left:
stack.append(node.left)
return res
def postorderTraversal(self, root):
# 注意:根节点为空,直接返回空列表
if not root:
return []
stack = []
res = []
while root or stack:
while root:
# 当前节点入栈
stack.append(root)
# 如果当前节点有左子树,继续向左子树找
if root.left:
root = root.left
# 如果当前节点无左子树,在右子树继续找
else:
root = root.right
# 跳出循环的条件是 root 为空,那当前栈顶元素为叶子节点。
# 弹出栈顶元素,并加入结果数组
cur = stack.pop()
res.append(cur.val)
if stack and stack[-1].left == cur:
root = stack[-1].right
# 否则证明当前栈顶元素无左右子树,那当前的栈顶元素弹出。
else:
root = None
return res
二叉树的插入
def insert_tree(root, data):
tmp_node = root
if root is None:
return root
while tmp_node:
if tmp_node.val > data:
if tmp_node.left is None:
tmp_node.left = TreeNode(data, None, None)
break
else:
tmp_node = tmp_node.left
else:
if tmp_node.right is None:
tmp_node.right = TreeNode(data, None, None)
break
else:
tmp_node = tmp_node.right
return root
获取二叉树最大深度
class Solution(object):
def maxDepth(self, root):
if root is None:
return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
二叉树最小深度
class Solution(object):
def minDepth(self, root):
from collections import deque
if root is None:
return 0
queue = deque()
queue.append(root)
depth = 0
last = root
while queue:
top = queue.popleft()
if top.left is not None:
queue.append(top.left)
n_last = top.left
if top.right is not None:
queue.append(top.right)
n_last = top.right
if top.left is None and top.right is None:
return depth + 1
if top == last and queue:
last = n_last
depth += 1
return depth + 1
二叉树的翻转
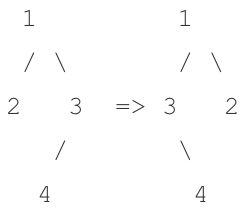
def mirror_tree(root):
if root is None:
return None
root.left = mirror_tree(root.left)
root.right = mirror_tree(root.right)
tmp = root.left
root.left = root.right
root.right = tmp
return root
二叉树是否相同
class Solution(object):
def isSameTree(self, p, q):
if p is None and q is None:
return True
elif p is None or q is None:
return False
elif p.val != q.val:
return False
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
判断二叉树是否轴对称
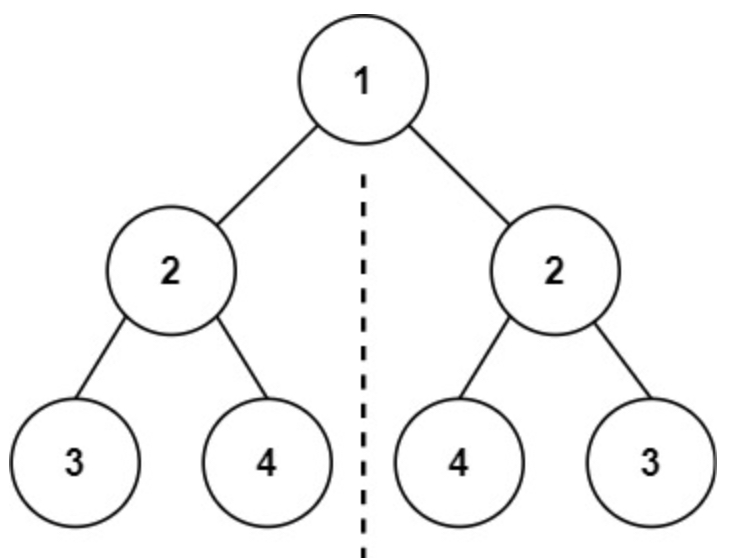
class Solution(object):
def check_same_tree(self, R1, R2):
if R1 is None and R2 is None:
return True
elif R1 is None or R2 is None:
return False
elif R1.val != R2.val:
return False
return self.check_same_tree(R1.left, R2.right) and self.check_same_tree(R1.right, R2.left)
def isSymmetric(self, root):
return self.check_same_tree(root, root)
这个问题十分巧妙,本来是一个树的判断,如果你的思维紧固到一个树上,那么就比较难做,但是当成两个树判断,这个题的难度一下子就的降低了不少。
二叉树的广度优先遍历
def breadth_first_traversal(root):
res = list()
queue = deque()
queue.append(root)
while queue:
top = queue.popleft() # 深度popleft->pop
res.append(top.val)
if top.left is not None:
queue.append(top.left)
if top.right is not None:
queue.append(top.right)
return res
按层遍历二叉树
def level_traversal(root):
t_set = list()
res = list()
q = deque()
q.append(root)
last = root
level = 0
while q:
top = q.popleft()
t_set.append(top.val)
if top.left is not None:
q.append(top.left)
n_last = top.left
if top.right is not None:
q.append(top.right)
n_last = top.right
while top == last and q:
last = n_last
res.append(t_set[:])
del(t_set[:])
level += 1
res.append(t_set[:])
return res, level
二叉树子树的判断
bool isSubtree(TreeNode *T1, TreeNode *T2) {
bool result = false;
if (T2 == nullptr) {
return true;
}
if (T1 == nullptr) {
return false;
}
if (T1->val == T2->val) {
result = dp(T1,T2);
}
if (!result) {
result = isSubtree(T1->left,T2);
}
if (!result) {
result = isSubtree(T1->right,T2);
}
return result;
}
bool dp (TreeNode *T1, TreeNode *T2) {
if (T1 != nullptr && T2!=nullptr && T1->val == T2->val) {
return dp(T1->left,T2->left) & dp (T1->right,T2->right);
}
if (T1 == nullptr && T2 == nullptr) {
return true;
}
return false;
}
二叉树是否平衡
bool IsBalanced(BinaryTreeNode* pRoot)
{
if(pRoot== NULL)
return true;
int nLeftDepth = TreeDepth(pRoot->m_pLeft);
int nRightDepth = TreeDepth(pRoot->m_pRight);
int diff = nRightDepth-nLeftDepth;
if (diff>1 || diff<-1)
return false;
return IsBalanced(pRoot->m_pLeft)&&IsBalanced(pRoot->m_pRight);
}
根据不同的顺序还原二叉树
从前序和中序还原二叉树
class Solution(object):
def buildTree(self, preorder, inorder):
def myBuildTree(preorder_left, preorder_right, inorder_left, inorder_right):
if preorder_left > preorder_right:
return None
# 前序遍历中的第一个节点就是根节点
preorder_root = preorder_left
# 在中序遍历中定位根节点
inorder_root = index[preorder[preorder_root]]
# 先把根节点建立出来
root = TreeNode(preorder[preorder_root])
# 得到左子树中的节点数目
size_left_subtree = inorder_root - inorder_left
# 递归地构造左子树,并连接到根节点
# 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root.left = myBuildTree(preorder_left + 1, preorder_left + size_left_subtree, inorder_left,
inorder_root - 1)
# 递归地构造右子树,并连接到根节点
# 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root.right = myBuildTree(preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1,
inorder_right)
return root
n = len(preorder)
# 构造哈希映射,帮助我们快速定位根节点
index = {element: i for i, element in enumerate(inorder)}
return myBuildTree(0, n - 1, 0, n - 1)
从中序与后序遍历序列构造二叉树
class Solution(object):
def buildTree(self, inorder, postorder):
def helper(in_left, in_right):
# 如果这里没有节点构造二叉树了,就结束
if in_left > in_right:
return None
# 选择 post_idx 位置的元素作为当前子树根节点
val = postorder.pop()
root = TreeNode(val)
# 根据 root 所在位置分成左右两棵子树
index = idx_map[val]
# 构造右子树
root.right = helper(index + 1, in_right)
# 构造左子树
root.left = helper(in_left, index - 1)
return root
# 建立(元素,下标)键值对的哈希表
idx_map = {val: idx for idx, val in enumerate(inorder)}
return helper(0, len(inorder) - 1)
检查平衡二叉树
class Solution(object):
def isBalanced(self, root):
def get_depth(root):
if root is None:
return 0
return max(get_depth(root.left), get_depth(root.right)) + 1
if root is None:
return True
if abs(get_depth(root.left) - get_depth(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(
root.right):
return True
return False
二叉树转单链表
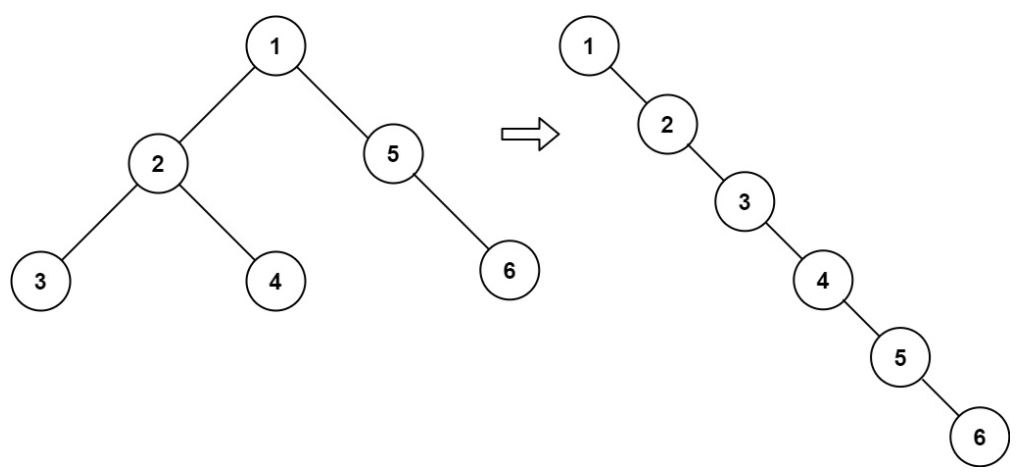
要求
- 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
class Solution(object):
def flatten(self, root):
def pre_order(root):
if root is None:
return []
return [root] + pre_order(root.left) + pre_order(root.right)
pre_list = pre_order(root)
for i in range(1, len(pre_list)):
pre, cur = pre_list[i-1], pre_list[i]
pre.left = None
pre.right = cur
二叉树的和
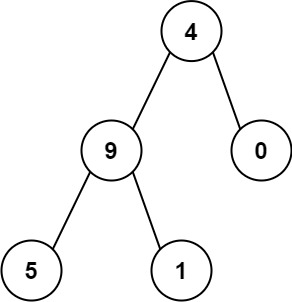
遍历二叉树的所有路径,且使用每个路径组成一个数字,最后求所有的数字的和。
class Solution(object):
def sumNumbers(self, root):
if not root:
return 0
total = 0
import collections
nodeQueue = collections.deque([root])
numQueue = collections.deque([root.val])
while nodeQueue:
node = nodeQueue.popleft()
num = numQueue.popleft()
left, right = node.left, node.right
if not left and not right:
total += num
else:
if left:
nodeQueue.append(left)
numQueue.append(num * 10 + left.val)
if right:
nodeQueue.append(right)
numQueue.append(num * 10 + right.val)
return total