接下来我们要介绍的算法都与图有关,那么我们就来先定义一下图。V表示网络中的节点,A表示网络中的弧。接下来咱们就来看下最小费用最大流问题。
OOI最优炉
OOI是位于威斯康星洲和亚拉巴马州的工厂制造家用烤面包炉。制成炉子会有火车运输到OOI位于孟菲斯和匹兹堡两个仓库之一,而后被分销到弗雷斯诺、皮奥利亚和纽瓦克的顾客站点。两个仓库也可以用公司的货车运用少量炉子。
我们的任务是做新型的E27炉子下个月的一个分销方案。每个工厂在此期间至多可以运送1000个炉子,且目前没有存货。弗雷斯诺、皮奥利亚和纽瓦克的顾客分别需要450、400和610个炉子。仓库间运送数量限制在25个炉子以内,但是产生费用,其他可行流的单位成本如下表
| 从/到 |
3孟菲斯 |
4匹兹堡 |
| 1威斯康星 |
7 |
8 |
| 2阿拉巴马 |
4 |
7 |
| 从/到 |
5弗雷斯诺 |
6皮奥利亚 |
7纽瓦克 |
| 3孟菲斯 |
25 |
5 |
17 |
| 4匹兹堡 |
29 |
8 |
5 |
然后各个工厂之间的关系如下。
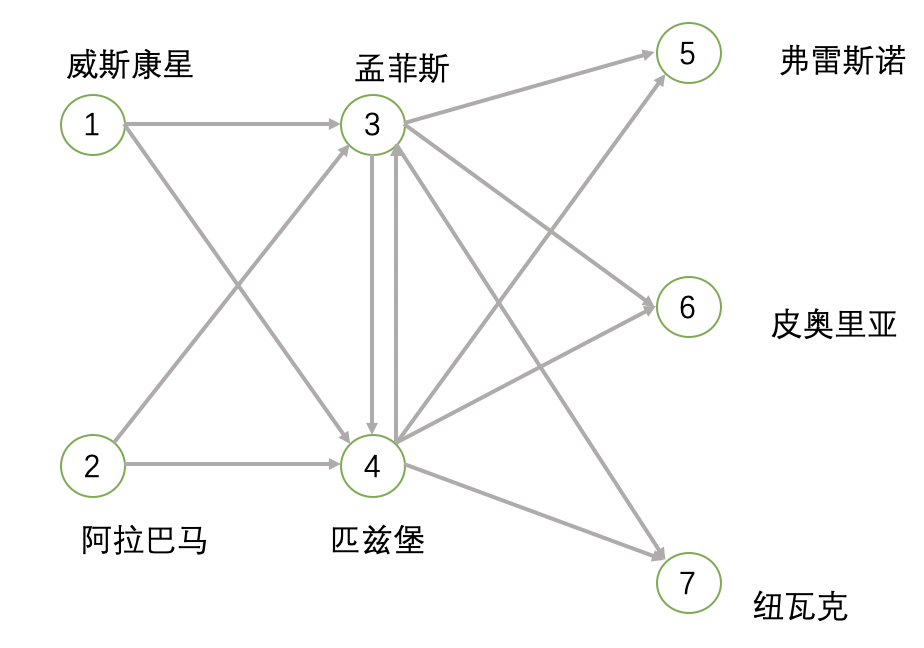
接下来咱们就来解决上面的问题,在最小费用流模型中。网络流的决策变量xi,j表示i到j的流量,ci,j表示i到j的成本,需要最小化的总费用为。
i,j∈A∑ci,jxi,j
一些约束也同样简单,流量必须非负才有意义,有时也可能会存在容量或者上限ui,j,就形成了约束0<xi,j<ui,j。在网络流问题中最主要的约束是节点上的流的平衡,更确切的说就是希望每个节点都满足。
总流入−总流出=指定的净需求
也就是
i,k∈A∑xi,k−k,j∈A∑xk,j=bk
bk表示节点k上指定的净需求量。
接下来我们来看看OOI问题的实际建模
min 7x1,3+8x1,4+4x2,3+7x2,4+25x3,5+5x3,6+17x3,7+29x4,5+8x4,6+5x4,7st.−x1,3−x1,4=−1000−x2,3−x2,4=−1000x1,3+x2,3+x4,3−x3,4−x3,5−x3,6−x3,7=0x1,4+x2,4+x3,4−x4,3−x4,5−x4,6−x4,7=0x3,4+x4,5=450x3,6+x4,6=500x3,7+x4,7=610x3,4<25x4,3<25xi,j>0
我们来解释一下这些约束都是干嘛的,第1个和第2个约束表示工厂源头生成1000个炉子可以运送出去,第3,4个约束表示孟菲斯和匹兹堡这两个节点的输入等于输出,第5,6,7表示每个工厂需要的炉子数。讲到这里大家是不是明白最小费用流的建模方式啦,是将网络中所有运输约束下完成目标优化的过程。
时间拓展流模型
咱们将上面的模型进一步加大难度,将一个流系统中的每个节点都建模转化为一系列的节点,每个节点对应一个时间区间。弧则反应某个特定时间内的流,或某个特定位置上的时间流。
某公司在任一个季度内可以制造1.5万个单位的产品,每千个产品费用是35美金,下表显示每千个产品分别运送公司两个顾客的成本以及每位顾客在不同季度所需要的产品。建设库存可以每千个单位季度8美元的费用存储在工厂中,请构建一个时间扩展网络来确定最优生产、分销库存计划。
| 顾客 |
运输费用 |
1季度费用 |
2季度费用 |
3季度费用 |
4季度费用 |
|
|
1 |
2 |
3 |
4 |
| 1 |
11 |
5 |
9 |
2 |
1 |
| 2 |
17 |
3 |
14 |
6 |
4 |
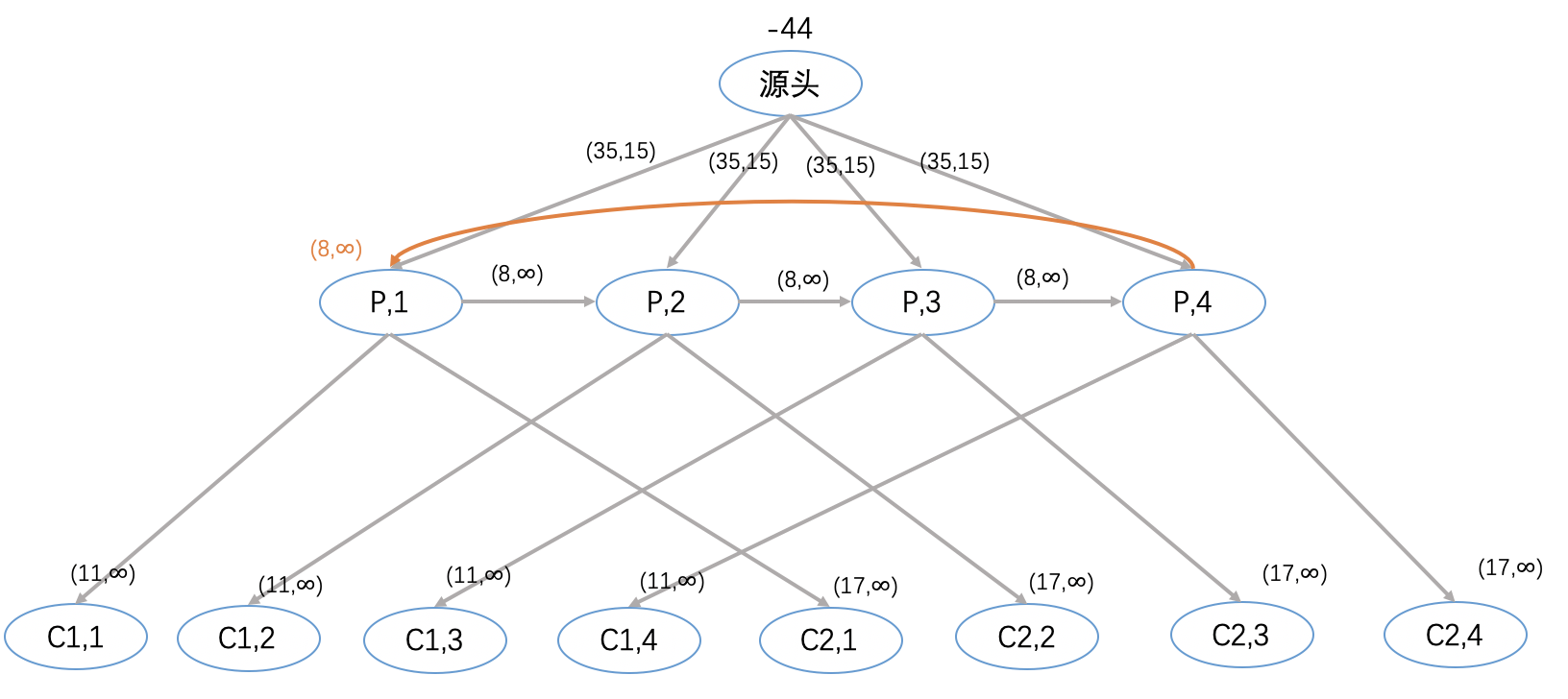
通过上面的描述,我们需要将变量处理为一个矩阵,将流量变量xi,j处理成矩阵x,将费用c和容量u都处理成对应的矩阵,并将净需求bk列入向量b,从而将最小费用流网络简化为如下的形式。
min c∗xs.t.Ax=b
这里的约束矩阵结构比较特殊,被称为节点一弧关联矩阵。
选址问题
这里顺便介绍一个选址问题。背景就是你如果想要开家店,那选择哪里比较合适呢? 这就是一个经典的选址问题。选址问题也有以下几种。
中值问题
目标是所有的需求点距离目标点的平均权重最短。
min i=1∑Nj=1∑Mdicijyij
一般应用在仓库选择上。
覆盖问题
覆盖问题一般应用在消防急救的地点选择, 目标是覆盖尽可能多的需求点。
其目标函数为在给定数量下的地点,覆盖尽可能多的需求点。
中心问题
在给定设备下, 求任意一个需求点与与他最近设施的最小最大距离,是优化最差的场景,一般是驻军、避难所的场景使用。
中心问题也叫 minmax 问题,是探讨如何在网络中选择 P 个服务站,使得任意一需求点到距离该需求点最近的服务站的最大距离最小问题。防止极端情况的出现。
min max Cj(X)
总而言之
本章咱们就把网络流的基本概念和例子说完啦,如果有什么问题欢迎留言提问哦,希望大家能将这些经典问题应用到自己的实际工作中。