本文来介绍精度更高的内部解释模型GAMI-Net。

GAMI-Net

GAMI-Net模型在广义加性模型的基础上，引入了神经网络与特征交互的信息，同时增加了稀疏性、遗传限制、边界清晰度的准则，这使得模型的精度和解释性得到进一步的提升。

模型定义

传统的广义加性模型对每个特征会拟合一个光滑函数$s_{j}(X)$，再将各个$s_{j}(X)$的结果累加得到最终结果，$s_{j}(X)$可以描述特征x与Y的非线性关系，但是精度不高。
GAMI-Net将神经网络引入进来使用神经网络$h_{h}(X)$替换成$s_{j}$，得到如下表达

$$g(E(Y|X))=\mu + \sum_{j=1}^{d} h_{j}(X_{j}) \tag{1.1}$$

g表示链接函数，$\mu$表示截距，$h_{j}(X_{j})$表示每个特征$X_{j}$对应的神经网络，使用梯度下降求解。模型结构如下

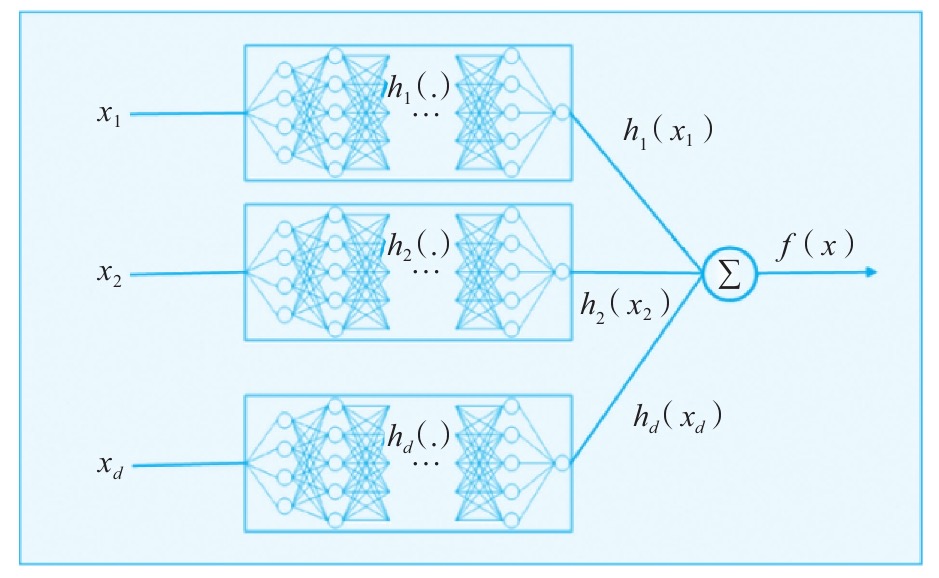
通过神经网络的拟合提升了模型精度，但是有时候特征之间的交互作用对模型结果也能产生巨大影响。为了进一步提升模型精度，GAMI又加入了交互信息。

$$g(E(Y|X))=\mu + \sum_{j=1}^{d} h_{j}(X_{j})+ \sum f_{jl}(x_{j},x_{l}) \tag{1.2}$$

和公式1.1不同的是加入了交叉项，$h_{j}(x_{j})$是单个特征与响应变量Y的关系，由一个神经网络表示，称为主效应。而$f_{jl}(x_{j},x_{l})$表示特征交叉与响应变量的关系，由一个神经网络表示，称为 成对交互项效应。

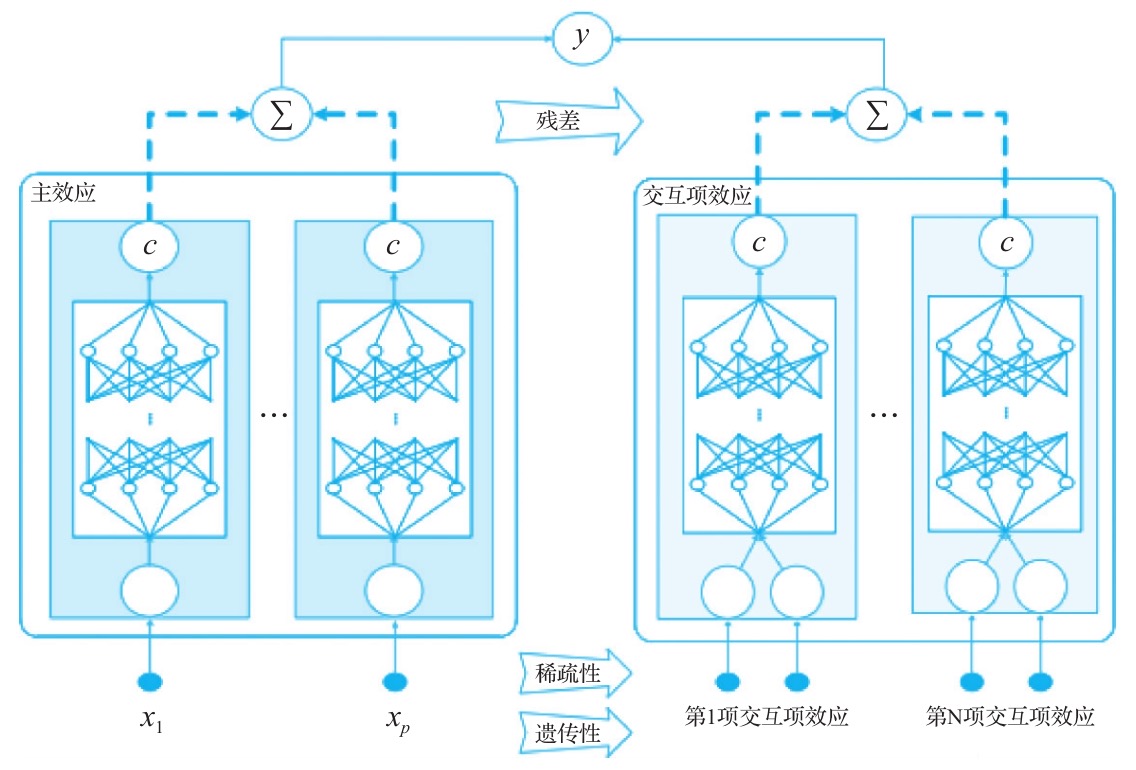
GAMI的3个重要准则

稀疏性

与含有冗余不重要的特征相比，精简的模型往往有更好的可解释性。所以GAMI加入了稀疏性准则来剔除不重要特征，只保留有效特征。通过变异程度来衡量。主效应变异程度h和交互项变异程度f如下

$$|| h_{j} || _{2}=\int h_{j}^{2}(X_{j}) dX_{j} \\ || f_{jl} || _{2}=\int f_{jl}^{2}(X_{j},X_{l}) dX_{j} dX_{l}$$

遗传限制

为了精简模型从而提高可解释性，GAMI只会保留重要的主效应和交互效应。由于交互效应是通过主效应产生的，因此如果不加以限制，不重要的冗余特征也会产生交互效应，这样模型的解释性就会变得无比混乱。 遗传限制指的是只有经过稀疏性准则筛选后的重要特征才能产生交互效应，从而避免了这个问题。
当然遗传性也有强弱之分，强遗传效应指的是两个主效应产生的交互效应都是重要特征。弱遗传效应是指其中一个特征是重要特征。

边界清晰度

当我们使用神经网络刻画交互效应与Y的关系时，如果不对子网络的输出结果加以限制，那么子网络输出结果可能带有单个特征的信息。例如下面这种情况

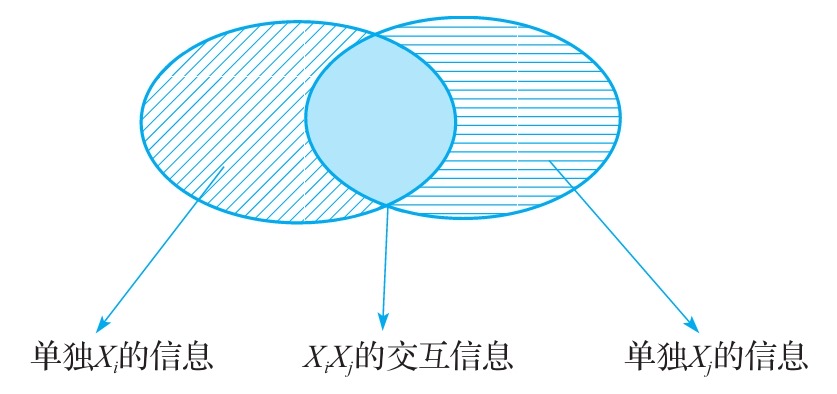
子网络的输出中不仅包含了$X_{i}, X_{j}$的交互特征，还分别包含了这两个特征的单独的效应。这个问题比较复杂，在介绍这个问题之前，咱们先来学习一个知识。

Functional Anova Representation

Functional Anova Representation思想是给定一个可积函数g，以及S个特征，那么g(x)可以表示为如下形式

$$g(X)=g_{0}+\sum_{j} g_{j}(X_{j})+\sum_{j<l} g_{jl}(X_{j}, X_{l}) +.. \tag{2.1}$$

$g_{0}$是常数，表示平均效应，$g_{j}(x_{j})$表示$x_{j}$的效应，$g_{jl}(X_{j}, X_{l})$表示交互项效应。
有了Functional Anova Representation这个思想，GAMI的思路十分简单，既然上面提到的直接计算出来的交互项是有干扰的，那么就将单独的主效应减去就好了。
具体就是将GAMI中主效应和交互效应对应的每个子网络都视为g(x).

$$g(x_{j})=g_{0}+g_{j}(X_{j})$$

为了获取单独的特征$X_{j}$的效应g_{j}(X_{j}), GAMI将每个子网络的输出$g_{j}(X_{j})$减去输出值的均值$g_{0}$,$g_{j}(X_{j})=g(X_{j})-g_{0}$, 从而使得主效应的值更加纯净。

对于交互项效应，将每个交互项对应的子网络中的g(x),此时g(x)中的变量有$x_{i},x_{j}$， 从而有

$$g(x_{i}, x_{j})= g_{0}+g_{j}(x_{j})+g_{i}(X_{i})+g_{ij}(x_{i}, x_{j})$$

同样为了获取$x_{i}，x_{j}$的交互效应，需要将没交互项效应的子网络输出值$g(x_{i}, x_{j})$减去$g_{0}+g_{j}(x_{j})+g_{i}(X_{i})$。为此，GAMI首先需要计算交互效应的两个边际均值。最后将交互效应输出值$g(x_{i}, x_{j})$减去两个均值再加上交互项总体均值$g_{0}$就得到了完整的交互项效应。

$$g(x_{i}, x_{j})-\int g(x_{j}, x_{i}) dX_{j} -\int g(x_{j}, x_{i}) dX_{i}+g_{0}=g_{ij}(x_{j}, x_{i}) \tag{2.2}$$

上面就是边界清晰度原则，从而保证整体的可解释性。

训练过程

GAMI的训练过程也比较简单，主要分为两步。

1. 先训练主效应，并保留重要的主效应。
2. 基于第一步得到的残差作为相应变量，已重要的主效应作为父代产生子代，基于之代训练交互效应，并保留交互效应

模型可解释性

全局可解释性

GAMI评估每个主效应和交互效应的变异程度来衡量重要率称为IR。

$$IR(j)=||h_{j}||_{2} /T \\ IR(j,i)=||f_{ij}||_{2} / T$$

通过这样的方式能够观察全局特征重要性

局部可解释性

对于局部可解释性其实就比较好理解，之前通过边界清晰度与原则能够计算每个主效应和交互效应的值，从而获得局部解释性。