咱们继续讲解可解释性机器学习,咱们开始一起来看看一些算法啦。先从简单的算法开始。
线性模型
线性模型经常被当成解释性模型的开山作。
Y=w0+w1X1+..+xnXn+σ(1.1)
通过模型回归w来解释每个维度对Y的影响,一部分是残差σ, 它是响应变量Y与的实际值与模型给出的预测值Yˉ的差距。另一部分是参数X的拟合程度。
分析
线性回归的优势主要体现
- 思路简单,易于实现,运用速度快
- 对于X与Y满足线性关系的数据很有效
- 解释性很强,建模结果有利于决策分析
缺点也比较明显
- 线性回归只能处理X和Y满足线性关系得数据,且要求σ满足正态分布,实际中很多数据是不支持的
- 与常见的机器学习相比,线性模型的精度较低。
广义线性模型
上文提到了很多数据分布是不符合线性回归的要求的,为了能让线性模型适用于更多的数据问题,可以对数据做一些转换,使转换后的数据满足线性回归的要求,这就是要讲的广义线性模型(Generalized liner model,GM)。
g(E(Y∣X))=XW,Y∣X∼f(Y∣X)(2.1)
g表示链接函数,满足平滑可逆的条件,f表示给定样本下的X下的Y的分布。 其核心思想是当Y或者σ不服从正态分布的情况下,可以找一个链接函数,同时学习合适的模型参数W,使得模型的线性部分挺相应的预测值,能够尽量的逼近Y的链接函数转化后的值。
当Y是离散数据的时候,选择二项式分布,取链接函数E(Y∣X)=ln1−YY,学习合适的参数W使得模型的线性部分输出值XW尽可能的接近Y经过连接函数转化后的值。就是XW=ln1−YY.
不过GM也不是万能的,当Y的分布服从指数分布的时候,它才能派上用场。
模型解释性
GM的同线性模型的可解释性保持一致,虽然中间经过了链接函数的转换,但是拟合的权重w依然可以用于解读特诊与结果的影响关系。
分析
GM的优势主要有
- 简单易于实现
- 不拘泥于Y的分布,使用范围更广
- 解释性比较强有利于决策分析
缺点如下
- 分布上虽然支撑的更大的指数分布,但是仍然有一些数据分布式不支持的
- 精度相比线性模型有提升,但是相比一般的机器学习模型仍然比较低。
广义加性模型
广义加性模型是解决广义线性模型只能只能进行线性拟合的缺点。
使用广义加性模型之前,一般会绘制一个X与Y的散点图查看二者的关系,当X和Y存在非线性关系的时候,但是又难以通过图像确定二者之间的非线性关系的具体形式,广义加性模型提供一种替代方案,它允许我们在预先不确定X和Y的关系的情形下,使用非线性平滑项拟合模型
g(E(Y∣X))=s0+j=1∑dsj(Xj)(3.1)
s0表示截距项, sj表示非参光滑函数, g表示连接函数。 例如Y是离散的变量服从泊松分布,取链接函数g(E(Y|X))=lnY时,学习合适的形式使得模型的加性部分输出值s0+∑j=1dsj(Xj),尽可能地接近相应变量Y经过连接函数转化后的值lnY。
实际应用中我们发现,并不是每个参数X和Y都是非线性关系,如果都使用平滑函数,那么计算量是巨大的,这个时候就出现了半参数广义加性模型
g(E(Y∣X))=s0+l=b∑qsj(Xl)+m=a∑pXmW(3.2)
其中a到p表示特征序号,b到q表示非线性特征序号。
可解释性
那么加性模型如何呈现可解释性,例如拟合出来的方程如下
Y=2.51+0.27x1+sx(X2)(3.3)
通过上面的拟合结果可以知道,x1每增加一个单位,Y增加0.27个单位,但是x2是通过s2来表达的,难以使用数学公式表达,但是可以将x2和s2的关系绘制出来。
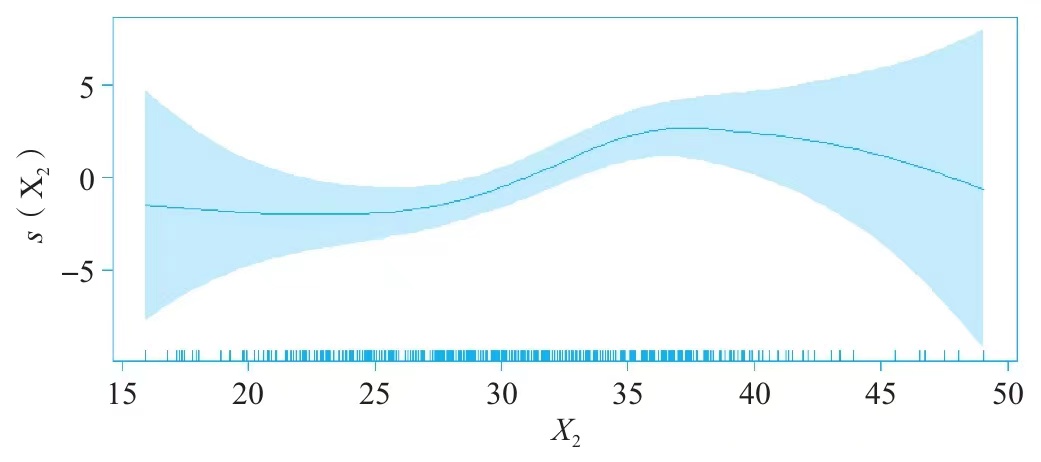
这个时候可以推测,随着x2的增加,Y呈现先轻微减少,然后再增加,最后再减少的趋势。
模型的分析
对于缺点就是,广义加性模型对比常用的模型,精度仍然不是十分高,而且过程中求解计算量巨大。
决策树模型
决策树模型相信大家一定不会陌生,也是做解释性的一个通用模型。
这里直接以解释性的视角说一下模型的特点
决策树模型的优点是
- 计算量小
- 模型结果通过规则产生,解释性好
缺点也是比较明显
- 容易产生一个过于复杂的模型进而过拟合
- 数据中微小的变化可能导致生成不同的树,稳定性较差。