业务特征选择

今天这篇文章就来讲讲特征选择的问题，特征选择是算法工程师一项再普通不过的任务，但是大家做的时候又是基本上靠感觉，或者更多的是看天吃饭，当然这本身也是一项非常难的任务，本文尝试将这个很难的任务解释清楚冰山一角，希望能对大家有帮助。

特征四象限

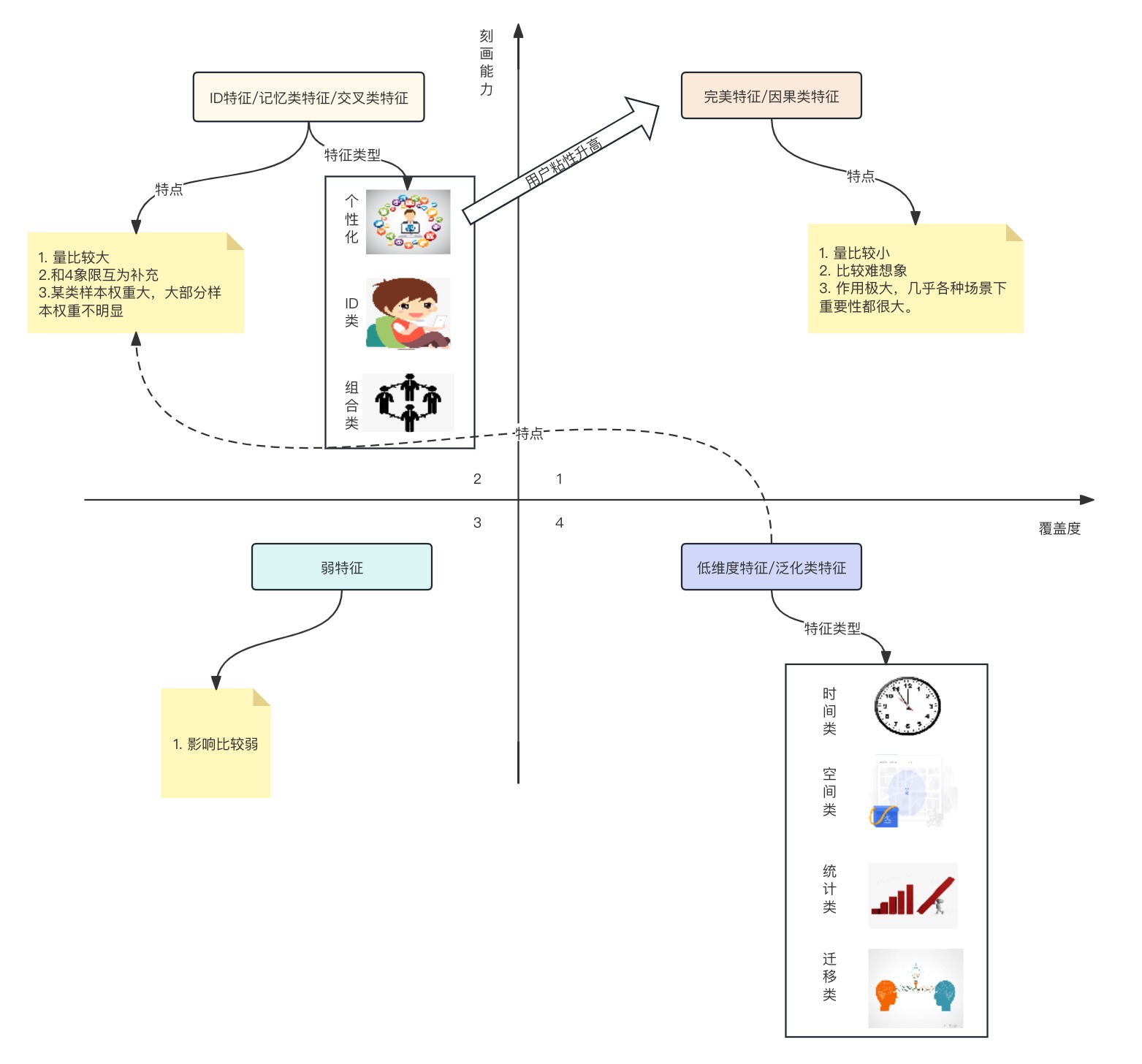
上图就是特征四象限，咱们接下来就针对这个图的一些标注进行解释，方便大家更加理解特征四象限到底在说什么？

特征覆盖度（横坐标）

先看上图的横纵坐标的两条线，其中横坐标就是特征覆盖度， 主要是表达在解决的过程中有多少样本的决策依赖这样一维特征，一方面体现特征的普适性，一方面体现特征的重要性。 因果类特征咱们就不多说啦，就是最终决定结果的最核心因素，统计类特征一般是比较有普适性的，所以它的覆盖性一般也比较强，时空类特征就属于这一类的特征。

刻画能力（纵坐标）

这是比较容易理解的特征类型，其实咱们就可以将这列特征理解为ID特征，这列特征的特点是某些样本的决策极度依赖这类特征，但是大部分其他样本几乎不依赖这类特征。 对于组合类特征也是，其实是想表达模型用户的习惯类特征。
对于一一些个性化类的业务，特别依赖这类特征。

现在说明白了这个象限的问题，就比较好理解这几种特征类型啦。

因果类特征（第一象限）

这类特征就是怎么做模型前一定要了解业务，并且理解业务。进而找到一些影响事情发生与否的关键特征，这类特征是稀少的，也是难以发现的，不同人对一个事物的理解是不同的，但是保证这个理解是对的，难度还是很大的。这也就是决定了这类特征的稀缺性，从另一方面也体现了算法工程师这个职业的特点，也是很多招聘需求里一定要提出来对数据敏感的要求。这类特征表示是模型对世界最原始的认知。

ID类特征（第二象限）

这类特征其实表达的是算法工程师对世界进一步的理解，如果说第一象限是物理世界的刻画和描述，第二象限是对物理世界接受和理解，理解不同的人有不同的决策，理解不同时空可以发生不同事情，这类特征体现是模型的包容和理解能力。
上图中有一个箭头，这箭头其实想表达的是，某一些特征在某一个象限并不是一成不变的，例如用户特性化特征随着用户粘性的变大，就有可能变成因果类的特征。

弱特征（第三象限）

这种特征大家一定十分常见，训练模型的时候经常在特征重要性排在最后，经常被大家忽视，其实这里需要澄清一点，弱特征不一定是没有用的，是有可能和其他特征组合以后，变成一个第二象限甚至是第一象限的特征的。 这一类特征体现的是模型对弱小的支持。
例如你要做一个模型，一个简单的例子可以是房屋的价格预测。$X_{1}$表示房屋的卧室数量,$X_{2}$表示房屋的厨房面积,在这个例子中，如果只考虑卧室数量或者只考虑厨房面积，它们可能对房价的预测影响都不大。然而，当将卧室数量和厨房面积两者结合起来考虑时，可能会更好地捕捉到房价的变化。

情景 1（只考虑卧室数量）： 卧室数量增加，并不一定会导致房价显著增加。可能存在很多其他因素（例如地理位置、楼层等）会影响房价。

情景 2（只考虑厨房面积）： 厨房面积的增加，也不一定直接导致房价上涨。房屋的整体结构和品质可能同样重要。

情景 3（考虑卧室数量和厨房面积）： 当卧室数量增加，同时厨房面积也增加时，可能表明这个房屋更大更适合家庭居住，从而对房价产生更显著的影响。

泛化类特征（第四象限）

这类特征其实更加普遍一些，例如时间和空间特征，几乎每个样本决策都依赖这样的特征， 但是这里特征的个性化不强，覆盖度是足够，当然如果你想提升模型的泛化性，应该尽可能的提升这类特征占比。
这一个象限表达的是模型的圆滑，当通过微观不能理解一个事物的时候，就从宏观理解它。

分场景讨论

如果你要做精排模型的时候，如何排序上面的4个象限呢？
第一类一定是“完美特征”
第二类应该是交叉类的特征，也就是第二象限的特征，因为到精排的模型，这里更关心个性化的部分，所以对于用户ID类特征要尽可能的敏感，并希望模型学出来尽可能细粒度的特征组合。

这个时候如果要做召回模型，你的特征选择应该怎么去选择呢？这里限定了我们希望扩大模型的召回，就是希望把相关的内容全部召回回来。
第一个类当然还是希望完美类特征
但是第二类的选择就是应该选择泛化特征了，也就是更偏好于第4象限，当然这个过程也不是特别绝对的， 其实应该是在2和4象限中选择尽可能靠近一1象限的特征。
这个时候因为你的核心目标是使用尽可能少的特征，召回更加topN的样本，然后使用精排进一步排序。

技术选择方法

覆盖率

它计算每个特征的覆盖率，就是特征在训练集中出现的比例，如果覆盖率较低对于模型的训练作用不大，可以直接剔除。

相关系数

一般使用皮尔斯相关系数，就是度量X和Y的线性相关性，这里需要注意一下，一定是线性相关性，对于相关度不高的特征可以剔除。

Fisher得分

对于分类问题，好的特征应该在同一个类别比较相似，不同类别差异较大，特征i的重要性可以使用Fisher得分表示

$$S_{i}=\frac{\sum_{j=1}^{K} n_{j}(\mu_{ij}-\mu_{i})^{2}}{\sum_{j=1}^{K} n_{j}p_{ij}^{2}}$$

其中$\mu_{ij}、p_{ij}$分别表示特征i在类别j中的均值和方法。$\mu_{i}$是特征i的均值，$n_{j}$是类别j的样本数。Fisher得分得分越高。特征在不同类别之间的差异性越大，同一个类别的差异度较小，特征越重要，反之就可以放弃啦

互信息

在信息论中，互信息就是相互熵，用来度量两个变量之间的相关性。互信息如果越高，就说明两个变量的相关性越高，相互独立，也就是可以尝试放弃其中一个特征。

最小冗余最大相关特征（mRMR）

由于单变量方法只能考虑单变量和目标变量的相关性。因此选择特征子集可能过于冗余。mRMR方法在进行特征选择的时候考虑到特征之间的冗余性，具体的做法就是跟已有的特征的相关性较高的冗余特征进行惩罚。这里的相关性可以使用之前的提到的互信息。

$$D(S,c)=\frac{1}{|S|} \sum_{f_{i} \in S} I(f_{i};c)$$

特征集合中所有的单特征变量$f_{i}$与目标变量的c的互信息$I(f_{i};c)$的平均值D(S,c)。

$$R(S)=\frac{1}{|S|^{2}} \sum_{f_{i},f_{j} \in S} I(f_{i};f_{j})$$

$$mRMR=max_{s}[D(S,c)-R(s)]$$

通过上述的优化问题可以得到一个特征子集合，在某些情况下mRMR可能对特征的重要性估计不足，因为只考虑单特征的之间的冗余性，没有考虑特征组合以后与目标值的相关性。
mRMR是一种典型的特征选择的增量贪心策略，某个特征一旦被选择就不会删除。mRMR可以改写成全局二次规划的优化问题。

$$QPFS=min[ax^{T}Hx-x^{T}F] \\ s.t. \\ \sum_{i=1}^{n}x_{i}=1$$

F为特征变量与目标变量（标签）的相关性，H为度量特征变量之间的冗余性矩阵。QPFS偏向于选择熵比较小的特征。

封箱方法

封箱方法实际上就是对特征集合进行枚举然后进行特征训练，计算量十分巨大。常用的特征子集搜索方式如下

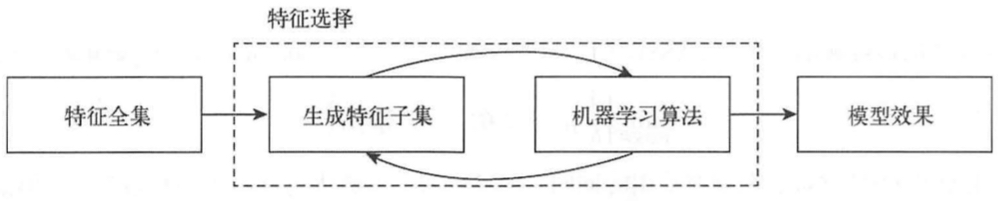
完全搜索

完全搜索分为穷举和非穷举。很明显穷举方式不是一个很好方式，一般我们使用定向搜索。

1. 选择N个得分较大的子集合。
2. 将其加入限制最大长度的队列里，每次从队列里取出得分最好的子集合，然后穷举将这个集合中加入某一个特征的效果。
3. 将这些特征集合加入队里内。

启发搜索

启发搜索分别前向选择和后向选择，前向选择是从空集开始每次加入一个特征训练。后向选择是从全集开始，每次减去一个特征训练。