本文介绍一下因果图中最经典的概念，d分离和前门准则和后门准则。

d分离

d分离在概率图中用来判断变量独立的一个很有效的方法，下面来看看D分离的定义。

当路径p被结点集Z，d-分离（或被blocked掉）时，当且仅当以下条件成立： 
1. 若p包含形式如下的链i->m->j 或i<-m->j，则结点m在集合Z中。
2. 若p中包含collider（碰撞点）i->m<-j,则结点m不在Z中且m的子代也不在Z中。

更进一步说，如果Z将X和Y d-separate，当且仅当Z将X，Y之间的每一条路径都block掉。
这里通过d分离也能够减少概率图的计算量。然后看看概率图中经典结构。

串行连接

图1串行连接中A通过事件B影响C，同样事件C也是用过事件B影响A。我们认为当证据B确定时，A、C条件独立。
称A和C被B节点D分离。

分叉连接

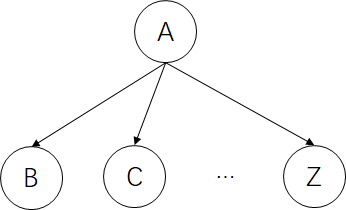
图2在分叉连接中A影响子节点，同样子节点通过A影响其他子节点。我们认为当A已知时，其各个子节点相互独立。称B、C、…、Z被A节点D分离。

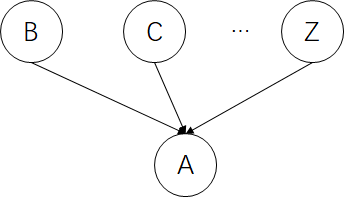
汇集连接（比较特殊）

在汇集连接中只有A节点未知时，我们才能认为其父节点们相互独立。

值得需要注意的是，如果某节点影响了节点A或者节点A的后代节点，我们认为其父节点们并不相互独立。

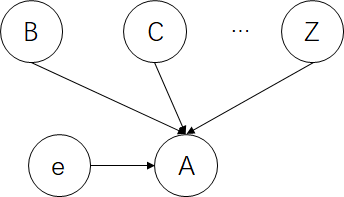
如上图，事件e直接影响了A，那么B、C…、Z并不独立

举例计算

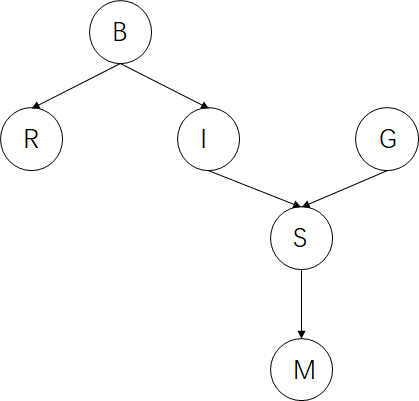
对于上图的形式，正常的联合概率计算为。

$$𝑃(𝐵,𝑅,𝐼,𝐺,𝑆,𝑀)=𝑃(𝑀|𝐵,𝑅,𝐼,𝐺,𝑆)∗𝑃(𝑆|𝐵,𝑅,𝐼,𝐺)∗𝑃(𝐺|𝐵,𝑅,𝐼)∗𝑃(𝐼|𝐵,𝑅)∗𝑃(𝑅|𝐵)∗𝑃(𝐵)$$

经过独立性的判断后，新的计算方式如下

$$𝑃(𝐵,𝑅,𝐼,𝐺,𝑆,𝑀)=𝑃(𝑀|𝑆)∗𝑃(𝑆|𝐼,𝐺)∗𝑃(𝐺)∗𝑃(𝐼|𝐵)∗𝑃(𝑅|𝐵)∗𝑃(𝐵)$$

后门准则

定义：给定有向无环图（DAG）中一对有序变量（X，Y），
如果变量集合Z（可以为空）满足： 
Z中没有X的后代节点。
Z阻断了X与Y之间的每条含有指向X的路径。
满足以上两点的Z，就称Z满足关于（X，Y）的后门准则。

如果因果图中满足了后门准则，那么X对Y的因果效应可以计算为

$$P(Y=y|X=do(x))=\sum_{z} P(Y=y|X=x,Z=z)P(Z=z)$$

一般而言，我们希望节点Z最好可以满足下面这些条件：

1. 阻断X和Y之间的所有伪路径（即所有指向X的路径）。
2. 保持所有X到Y的有向路径不变。
3. 不会产生新的伪路径。（例如condition在collider或者其后代上，可能就会产生一条新的伪路径）。

举例

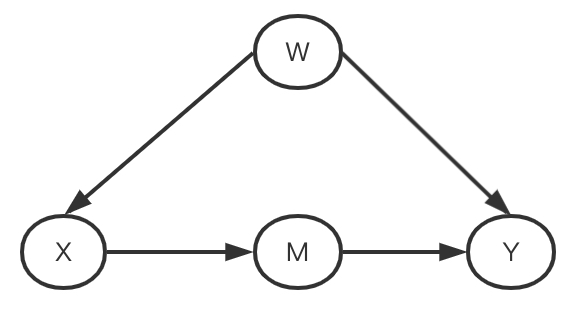
如图5所示，从X到Y有两条路径，第一条是X-M-Y，第二条是X-Ｗ-Y。我们想要估计X对Y的因果效应，就应该要阻断第二条路径。根据上面的后门准则，我们可以发现W满足后门准则，所以我们校正Ｗ（或者说Condition在W上），就可以得到X对Y的因果效应。

进一步举一个生活中的例子。

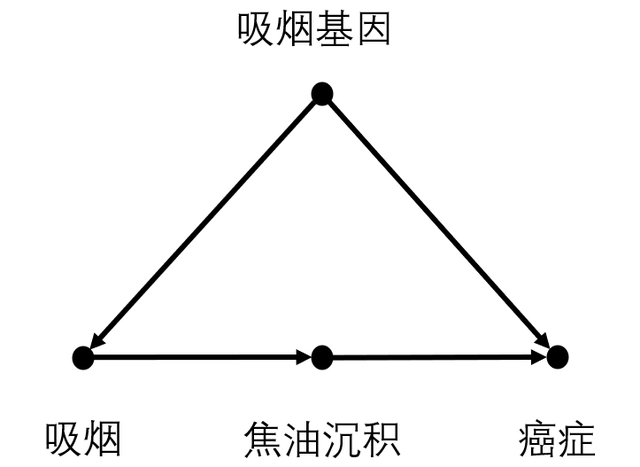
研究“吸烟”（原因变量）对“癌症”（结果变量）的影响为例，“吸烟->焦油沉积->癌症”为因果路径，其中，“焦油沉积”为中间变量。“吸烟<-吸烟基因->癌症”为一条从“吸烟”到“癌症”的后门路径，该路径包含指向“吸烟”的箭头，其中“吸烟基因“为混淆变量。此外，整个因果图中只有一条从“吸烟”到“癌症”的后门路径。因此，控制了“吸烟基因”，我们就阻断了从“吸烟”到“癌症”的所有后门路径。
最后计算吸烟和癌症的因果效应如下。

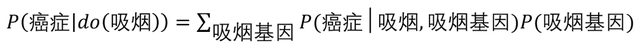
反概率权重法

不知道大家发现了没有，如果按照原始的公式计算，有个时候因为Z的取值过多，对样本分成过细，直接导致计算出来的概率是不可以用的。所以我们会采用简单的反概率权重法。

$$P(Y=y|do(x))=\sum_{z}P(Y=y|X=x,Z=z)P(Z=z)\\ =\sum_{z}\frac{P(Y=y|X=x,Z=z)P(Z=z)P(X=x|Z=z)}{P(X=x|Z=z)} \\ =\sum_{z} \frac{P(Y=y,X=x,Z=z)}{P(X=x|Z=z)}$$

经过上面的推导，我们发现这个时候只需要将以Z为条件的组合分别乘以$\frac{1}{P(X=x|Z=z)}$,再按照z取值的组合进行求和就好，这就是 反概率权重法， 一般这个权重也被称为倾向性得分。

前门准则

定义：如果一个变量集合Z满足以下条件：
Z切断了所有X到Y的有向路径。
X到Z没有后门路径。
所有Z到Y的后门路径都被X阻断。
则称变量集合Z满足有序变量（X，Y）的前门准则。

如果因果图中满足前门准则，那么X对于Y的因果效应是可识别的。

$$P(Y=y|X=do(x))=\sum_{z} P(Z=z|do(X))P(Y=y|do(Z)) \\ =\sum_{z} P(z|x) \sum_{x'}P(y|x',z)P(x')$$

这里仍然以图5为例，，即使W是不可观测的，那么我们依然可以使用前门准则，估计X对于Y的因果效应。
这里可以在引申一下，这里和之前提到的处置效应有什么关系吗？
咱们可以回顾一下

$$ATE=wATT+(1-w)ATU$$

可以发现，这里提到的w就是p(z), 而ATT和ATU表示的是接受人群的处置效应和非接受人群的处置效应。

举例

前门路径就是指从X到Y的直接因果路径，即上述：“吸烟->焦油沉积->癌症“的路径。当因为缺乏必要的数据而无法阻断某条后门路径时，就要通过前门准则，将X对Y的因果效应分解为X对Z的因果效应和Z对Y的因果效应。
在吸烟的案例中，假设我们无法对吸烟基因进行测量，但是可以获取”吸烟“，”焦油沉积“，以及“癌症”这三个变量的数据。这时，我们将“吸烟”对“癌症”的平均因果效应P(癌症|do(吸烟))，转化为P(焦油沉积|do(吸烟))和P(癌症|do(焦油沉积))的加权。在计算P(焦油沉积|do(吸烟))时，路径“吸烟<-吸烟基因->癌症<-焦油沉积”中 “癌症”处出现的对撞天然地阻断了这条后门路径。在计算P(癌症|do(焦油沉积))时，存在后门路径“焦油沉积<-吸烟<-吸烟基因->癌症“，通过控制”吸烟“可以阻断。利用前门准则，最终可以得到：