因果推断(∞)--因果推断框架总结

之前写了那么多因果推断的博客，这篇博客做一个大的总结。以前写了好多散点的知识，这篇文章就要将这些散点的知识进行一次汇总。
宏观上看因果框架分为两个部分，一个是结构因果框架，一个是潜因果框架。本文主要讲解潜因果框架的内容。之前介绍了很多散点的知识，这一节中会逐渐找到这些知识的归属地。

结构因果框架

结构因果框架主要包含因果图和结构方程的内容。之前介绍了很多相关的内容，这里就不会一一介绍了。

结构因果框架中的工具变量

工具变量是一种通用的用过推断方法，能够在两种框架中都得到使用，解决的主要问题是永远存在一个混淆变量是不可观测的。
图1-1
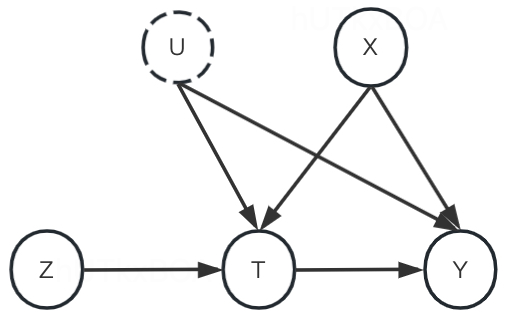
T是处置变量，Y是结果变量，U是不可观测变量，Z是工具变量，X是特征变量。前门准则、后门准则、do算子都是在这个框架下产生的方法。

工具变量的定义

Z是一个工具变量符合的两个条件分别是

Z是外在变量。 $X \not \perp Y|Z$ .
以观测到特征以及处置变量为条件，Z和Y是相互独立的。 $Z \perp Y|do(T),X$
第二条想说的就是工具变量与结果变量之间有一条经过处置变量T的路径。那么看起来Z是负责这个条件的，这个时候在结构因果框架中如何进行因果推断呢?使用结构因果因果方程进行表示。

T=aZ+bU+cX+\alpha \\ Y=dT+eX+fU+\beta \\

其中小写的字母都是参数和权重，大写的字母表示值。
将第一个公式带入第二个公式后。

Y=d(aZ+bU+cX+\alpha)+eX+fU+\beta \\ =adZ+acU+dcX+d\alpha+eX+fU+\beta \\ =adZ+U(ac+f)+X(dc+e)+d\alpha+\beta

E(Y|Z=1)-E(Y|Z=0)=ad \\ E(T|Z=1)-E(T|Z=0)=a

最后d的表达如下

d = \frac{E(Y|Z=1)-E(Y|Z=0)}{E(T|Z=1)-E(T|Z=0)}

潜因果框架

潜因果框架是一个更加强调从个体处置效应入手的一种因果分析框架。且潜在因果框架需要满足如下的一些假设。

上面的强可忽略性假设就是能为下文的工具性变量进行因果推断所用。这个假设是用于解决内生性问题的一种方法。通过引入工具变量、断点回归设计、倾向得分匹配等方法，在满足条件独立性假设的前提下，可以通过观测到的特征或部分特征来估计处理对结果的因果效应。

内生性和外生性

内生性（Endogeneity）：

内生性指的是变量之间存在一种内在的相互依赖关系，使得我们无法准确地分离因果效应。当两个或多个变量之间存在内生性时，观测数据可能无法提供无偏的因果估计。内生性可以导致因果关系的混淆和混杂，使我们无法确定变量之间的真实因果关系。

举个例子，假设我们研究学生的学习时间和考试成绩之间的关系。如果我们发现学习时间和考试成绩相关，那么这种相关性可能是因为学习时间影响了考试成绩，也可能是因为考试成绩影响了学习时间。在这种情况下，学习时间和考试成绩之间存在内生性，我们无法准确确定哪个是因果变量。

外生性（Exogeneity）：

外生性指的是变量之间不存在内在的相互依赖关系，使得我们可以将因果效应准确地归因于某个特定的变量。当变量之间满足外生性时，我们可以使用观测数据来推断因果效应，并获得无偏的因果估计。

举个例子，假设我们研究一个药物对疾病治疗效果的影响。如果我们进行了随机对照实验，将患者随机分为治疗组和对照组，那么药物的分配就是外生的，不受其他因素的影响。在这种情况下，我们可以将观察到的治疗效果归因于药物的作用，因为药物的分配是外生的，与其他潜在因素独立。

潜因果框架中的工具变量

在潜因果框架中，从个体出发，其中ITE的表达如下

Y_{i}(1, T_{i}(1))-Y_{i}(0, T_{i}(0)) \tag{2.1}

其中1和0表示工具变量Z的取值，这种表达强调工具变量对结果变量的影响。接下来推导如下表达。 $Y_{i}(Z)$ 表示受到工具变量影响的潜结果， $Y_{i}^{T}(Z)$ 表示受处理变量影响的结果。

Y_{i}(1, T_{i}(1))-Y_{i}(0, T_{i}(0))\\ =Y_{i}(T_{i}(1))-Y_{i}(T_{i}(0)) \\ =(Y^{1}_{i}T_{i}(1)+Y^{0}_{i}(1-T_{i}(1)))-(Y^{1}_{i}T_{i}(0)+Y^{0}_{i}(1-T_{i}(0))) \\ =(Y^{1}_{i}-Y^{0}_{i})(T_{i}(1)-T_{i}(0)) \tag{2.2}

第一个等式是工具变量的形式，第二个等式是一致性的推导( $Y_{i}=T_{i}^{1}-(1-T)Y_{i}^{0}$ ),第三个等式就是简单的数学推导啦，实际使用的时候可以使用E期望。

E[(Y_{i}^{1}-Y_{i}^{0})(T_{i}(1)-T_{i}(0))] \\ =E[Y_{i}^{1}-Y_{i}^{0}|T_{i}(1)-T_{i}(0)=1]P(T_{i}(1)-T_{i}(0)=1)-E[Y_{i}^{1}-Y_{i}^{0}|T_{i}(1)-T_{i}(0)=-1]P(T_{i}(1)-T_{i}(0)=-1) \tag{3.1}

这里引入单调性原则，处理变量的值随着工具变量的值的增大不会减小， $T_{i}(1)>=T_{i}(0)$ , 也就是说 $P(T_{i}(1)-T_{i}(0)=-1)=0$ , 就是说当工具变量的变化不引起处置变量的变化的请求下，对结果变量不会造成影响，那么公式3.1进行变形。

E[Y_{i}^{1}-Y_{i}^{0}|T_{i}(1)-T_{i}(0)=1] \\ =\frac{E[(Y_{i}^{1}-Y_{i}^{0})(T_{i}(1)-T_{i}(0))]}{P(T_{i}(1)-T_{i}(0)=1)}\\ =\frac{E[(Y_{i}^{1}-Y_{i}^{0})]}{E(T_{i}(1)-T_{i}(0))} \tag{3.2}

等式的左边被称为局部因果效应（LATE），就是说满足单调性的个体的期望。等式的最后表示概率量转变为统计量， $(T_{i}(1)-T_{i}(0))$ 一定是产生了效应的个体，设置成1.
使用潜因果框架的假设 $Z \perp Y_{i}(1), Y_{i}(0),T_{i}(1),T_{i}(0)$ ,进一步得到公式3.3

E[(Y_{i}^{1}-Y_{i}^{0})]=E(Y_{i}^{1})-E(Y_{i}^{0}) \\ =E(Y_{i}^{1}|Z=1)-E(Y_{i}^{0}|Z=0) \\ =E(Y|Z=1)-E(Y|Z=0) \tag{3.3}

类似的 $E[(T_{i}^{1}-T_{i}^{0})]=E(T|Z=1)-E(T|Z=0)$ ,那么公式3.2最新的形式如下：

E[Y_{i}^{1}-Y_{i}^{0}|T_{i}(1)-T_{i}(0)=1]=\frac{E(Y|Z=1)-E(Y|Z=0)}{E(T|Z=1)-E(T|Z=0)} \tag{3.4}

是不是很熟悉，和结构因果框架的形式表现就一致啦。不过需要注意的是在潜因果框架中存在许多的假设。

双重差分(DID)

这里介绍双重差分的的一个典型的例子，目标是要探索涨工资对快餐业的因果效应，A城市的工资上涨，然后选择与A城市比较近的B公司没有上涨的城市作为对照组。
对于单位i而言，将观测到的结果 $C_{i}$ 和干预后的实验组结果 $Y_{i}(1)$ ,而对于单位j，我们将观测前结果 $C_{j}$ 和干预后对照组结果 $Y_{j}(0)$ 。双重差分的基本思路是用单位j的对照组 $Y_{j}(0)$ 和干预前结果 $C_{i}，C_{j}$ 之间的关系来推断单位i在干预后的结果 $Y_{i}(0)$ ，这样就能评估出平均的因果效应。

接下来可以看一个推导过程，双重差分方法进行因果推断，接下来我们来看下面这个因果图。

双重差分

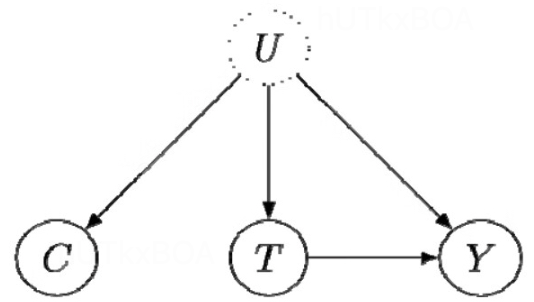
处理变量T对干预前的因果效应C是不会有因果效应的， $P(C|do(T)=1)=P(C|do(T)=0)$ ,但是因果混淆变量U的出现，我们会发现能发现实际的期望分布是 $E(C|T=1)-E(C=0)$ 实际的值不为0.且反应到了C<-U->T的后门路径上的相关性。这种相关性被称为加性混淆效应，接下来也给出来双重时序差分的一个最重要的假设加性伪混淆效应假设。

处理变量T和结果变量Y的加性混淆效应与处理变量T和干预前结果变量C的加性混淆效应大小是相同的。

E(Y(0)|T=1)-E(Y(0)|T=0)=E(C|T=1)-E(C|T=0) \tag{4.1}

进一步解释一下对于因果推断中的条件期望值 E(Y(0)|T=1)，这个表示的是在某个个体已经接受了处理（T=1）的情况下，对于该个体来说，如果他没有接受处理（T=0），其随机变量 Y 的期望值是多少。这个表示的是一种“反事实”情况。
进一步可以得出

E(Y(1)-Y(0)|T=1) \\ =(E(Y|T=1)-E(Y|T=0))-E(C|T=1)-E(C|T=0) \tag{4.2}

从上图能够看出E(Y(1)-Y(0)|T=1) ，包含着实际的因果效应和C<-U->T后门路径带来的混淆效应，所以公式4.2公式，使用(E(Y|T=1)-E(Y|T=0))的平均因果效应减去混淆进来的C<-U->T因果效应。双重差分的局限性时假设我们能观测到两个单位在两个时间步中的C，T，Y（干预前结果，处理变量，结果变量）。要求一部分是得到干预的结果。在第二个时间步进入实验组。另一部分则是两部分都进度对照组，还有满足加性伪混淆假设。

一个例子

接下来咱们一起来看一个简单的图就能理解啦，看起来很难，实际用起来十分简单。计算关系如下。

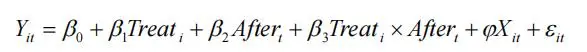
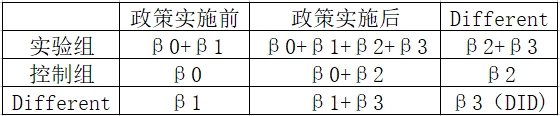
其中，i 代表个体，t 代表时间。Treat i 是分组虚拟变量，如果个体 i 属于实验组，则 $Treat_{i} =1$ ；否则 $Treat_{i} =0$ 。 $After_{t}$ 是分组虚拟变量，时间 t 在政策事件发生后，则 $After_{t}=1$ ；否则 $After_{t}=0$ ； $Treat_{i} \times After_{t}$ 为交互项，其系数β3即为双重差分模型重点考察的政策实施的净效应。
DID
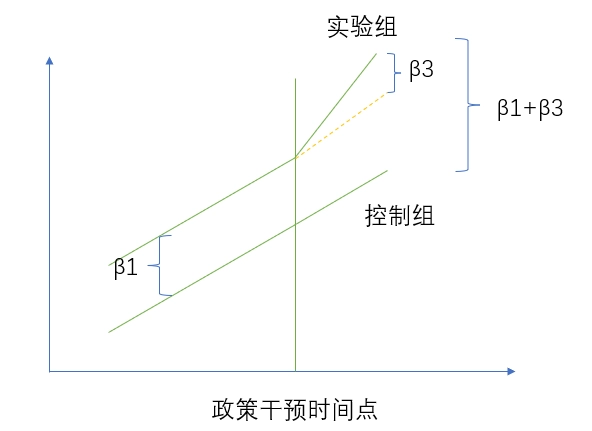
上图使用DID进行计算的时候，就如下图所示。