不知道大家注意了没有，因果推断的假设往往是通过样本去做因果推断，如果样本是随机抽抽取的，那么我们得出的结论也是准确的。而现实的生活中我们的样本往往是自行选择的，带来的影响是我们不能很好的估计它的平均处置效应。这里我可以举一个例子，我们想通过抽取样本来分析智商对大家成绩的影响，所以我们从上大学的样本中抽取了若干样本，但是我们发现有一些智商足够但是没有上大学的样本学校成绩是缺失的。那么这就给这个估计带来一定的影响。本章要解决的就是这样的问题，是不是恶心的要死。
Heckman
我们一般通过Heckman方法来解决此类问题，当然Heckman算法还有一些变种，本章就介绍最基本的Heckman算法，为大家提供解决这样问题的思路。
模型定义
首选模型分为选择方程和结果方程。
结果方程
$$
Y_{i}^{*}=\alpha + X_{i}\beta+e_{1i}
$$
选择方程
$$
D_{i}^{*}=Z_{i}'r+e_{2i}
$$
$$
\begin{equation}
\left\{
\begin{array}{ll}
D_{i}=1, if\ D_{i}^{*}>0 \\
D_{i}=0, if\ D_{i}^{*}<=0 \\
\end{array}\right.
\end{equation}
$$
样本中观测结果为
$$
\begin{equation}
\left\{
\begin{array}{ll}
Y_{i}=Y_{i}^{*}, if\ D_{i}=1 \\
Y_{i} 缺失, if\ D_{i}=0 \\
\end{array}\right.
\end{equation}
$$
咱们开始解释变量含义啦，$X_{i}$是决定结果的解释变量，$e_{1i}$表示结果方程的干扰项，$e_{2i}$样本选择干扰项，$X_{i}$和$Z_{i}$为外生变量，其中$Z_{i}$包含$X_{i}$的所有变量并且至少一个变量不在$X_{i}$。
在算法选择模型中，直接假设二者是如下关系。
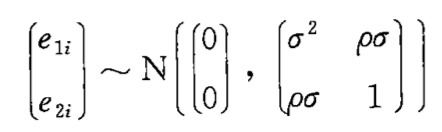
也就是说干扰项满足均值为0的二元正态分布，$e_{1i}$方差为$\sigma$,$e_{2i}$方差为1,二者相关系数为$\rho$.
说到这里你可能蒙了，你就给我看这个？太抽象了吧。是的，那咱们来举个例子吧。
对上咱们开头举得那个例子。
结果方程为
$$
score=\alpha + IQ \beta+e_{1i}
$$
表示IQ与分数的关系。
选择方程为
$$
Utility_{i}=r_{0}+r_{1}IQ_{i}+r_{2}Home+e_{2i}
$$
$$
\begin{equation}
\left\{
\begin{array}{ll}
D_{i}=1, if\ Utility_{i}^{*}>0 \\
D_{i}=0, if\ Utility_{i}^{*}<=0 \\
\end{array}\right.
\end{equation}
$$
上个方程中加入了Home表示家庭教育对是否上大学的影响因素。
这里你可能好奇的是Heckman是如何解决样本选择偏差的呢？感觉没啥关系呀。
那么咱们给给出一些数学推导的过程。
自选择样本观测数据结果的条件期望函数为
$$\begin{gathered}E(Y_{i}|样本,X_{i}) \\
=E(Y_{i}|D_{i}=1,X_{i}) \\
=E(\alpha+X_{i}\beta+e_{1i}|Z_{i}r+e_{2i}>0,X_{i}) \\
=\alpha+X_{i}\beta+E(e_{1i}|e_{2i}>-Z_{i}r,X_{i}) \\
=\alpha+X_{i}\beta+E(e_{1i}|e_{2i}>-Z_{i}r) \\\end{gathered}$$
因为$e_{1i}$和$_{2i}$是相关的。所以$E(e_{1i}|e_{2i}>Z_{i}r)!=0$.如果想要估计出$\beta$就要把$E(e_{1i}|e_{2i}>Z_{i}r)$控制掉，那么就要加入一个新的干扰项。
$$
Y_{i}=\alpha+X_{i}\beta+E(e_{1i}|e_{2i}>-Z_{i}r)+v_{i}
$$
$v_{i}$就是新的干扰项，增加新的控制项的情况下，$E[v_{i}|样本,X_{i}]=0$.那么问题来啦，$E(e_{1i}|e_{2i}>Z_{i}r)$是多少呢？其实我们也不必亲自观测到$e_{1i}、e_{2i}$,因为我之前给出一个假设，二者服从二元正态分布，会有如下关系。
$$\begin{gathered}E(e_{1i}|e_{2i}>Z_{i}r)=\rho \sigma \lambda(Z_{i}r) \\
=\rho \sigma \frac{\phi[\frac{-Z_{i}r}{\sigma}]}{1-\Phi[\frac{-Z_{i}r}{\sigma}]}\end{gathered}$$
这里的$\lambda$称为逆米尔斯比例（IMR）。$\phi$表示正态分布概率密度函数，$\Phi$正态分布累积函数。
所以第一阶段，使用Probit模型估计样本选择方程
$$
Pr(D_{i}=1|Z_{i})=Pr(e_{2i}>-Z_{i}r|Z_{i})=\Phi(Z_{i}r)
$$
这样就得到r的值，然后把r的值，然后把r带入IMR公式，为每个个体计算出IMR。
第二阶段使用样本数据将$Y_{i}$对$X_{i}\beta$和$\lambda_{i}$回归。
$$
Y_{i}=\alpha+X_{i}\beta+\rho \sigma \lambda_{i}+v_{i}
$$
从而我们得到了相对一致性的估计。本章我们又解决了因果推断的一个大问题，希望大家不要遇到这样的问题。