不知道大家发现了没有,我们在谈论因果推断的时候往往都是构造一个随机环境,从而得到一个置信度较好的结果,但是因为种种原因,我们现实中能够提供随机环境的机会并不多,那么断点回归实际上就是提供了一种在非随机实验的环境下如何去做因果分析。因果推断的思路十分好理解,其实就是我们找到观测特征的那个临界点,观察临界点前后的结果变量的变化,从而起到了估计处置效应的作用。
断点回归的理解
我们来考虑这样一种场景,假设政府有一个针对低收入人群的医疗政策。政府规定只对收入水平低于或者等于50的病人提供这项治疗,收入高于50的不能接受治疗,那么收入50就成为这个问题的划分点,也称为断点,平均观测结果如下
E(Yi∣Xi)={E(Yi(0)∣Xi) E(Yi(1)∣Xi) X>50X<50
对于收入值Xi不存在同时接受治疗和不接受治疗的观测值,所以这与之前讲到的匹配方法中是相违背的,也就是不存在共同支撑域。那么怎么来估计处置效应呢?
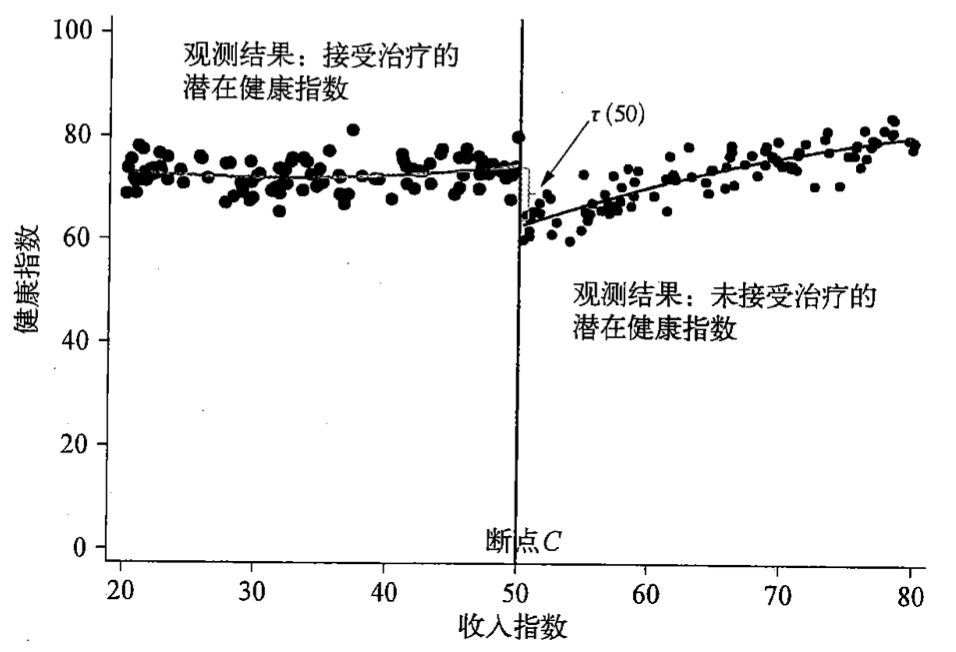
从上图中我们能找到断点C,也就是50,那么我们的思路是找到断点左边一点点的值作为小于50的结果,例如收入49.9.同样的,找到右边一点点值作为右侧的估计效应,这样我们是不是可以近似的计算出这个处置效应。
l(50)=E(Yi(1)∣Xi=50)=E(Yi(0)∣Xi=50)≈E(Yi(1)∣Xi=49.9)=E(Yi(0)∣Xi=50.1)
是不是豁然开朗,原来还可以这么玩。但是断点回归有一个致命的缺点是,断点回归只适用于断点出的人群,不能推广到其他个体,这就是他的局限性。
断点回归的数据条件
- 配置变量,配置变量是个体的一个连续特征变量,就是上面提到的收入
- 断点
- 观测结果。
汇总一下
最后一章,咱们就这么愉快的结束吧,其实大家发现没有其实很简单,但是却能为你分析数据的时候提供不一样的思路。例如我们上节提到的双重差分,可以结合AA和AB的实验结果来看待实验效果,不再苦恼于我知道这么做,但是不知道为什么的尴尬。希望这个系列的讲解能给他大家打开一个新的思路。