本章节中咱们来聊聊如何发现一个因果结构,先给出因果的框架长成什么样子。
因果结构的定义
一组变量V的因果结构是一个有向无环图,其中每个节点对应的V的一个变量,每个连接表示对应变量之间的直接函数关系。
而因果模型的定义是依照因果结构而来的。
因果模型是由因果结构D,以及与D相容的参数集合θ组成的M=[D,θ]。参数集合θ中每个变量xi∈V赋予函数xi=f(pai,μi),这里每个 μi赋予概率值p(μi),其中pai是D中xi的父代变量,μi是依据p(μi)分布的随机扰动,所有的μi相互独立。
这里的独立扰动这个假设使得模型具有马尔可夫性, 就是说D中的父代变量为条件的时候, 每个变量都独立于它的所有非后代变量。
接下来咱们就要进入一波晦涩的定义啦。咱们用加粗字体表达定义的名字。
因果结构
潜在结构的定义是L=[D ,O], 其中D是V上的因果结构,而O∈V是一个观测变量集合。
潜在结构L=[D ,O]优于潜在结果L’=[D’ ,O]当且仅当D’可在O上模拟D,就是说对于每个参数θD,存在θD′使得P(D′,θD′)=P(D,θD)。两个潜在的结构是等价的。称为结构偏好。
从上面的定义能够看出,其实期望的因果结构具有一些特性,极小性,尽可能简单的表达一个因果结构。 另一个特性是一致性,就是潜在结果L能够解释一个结果的所有相关关系。
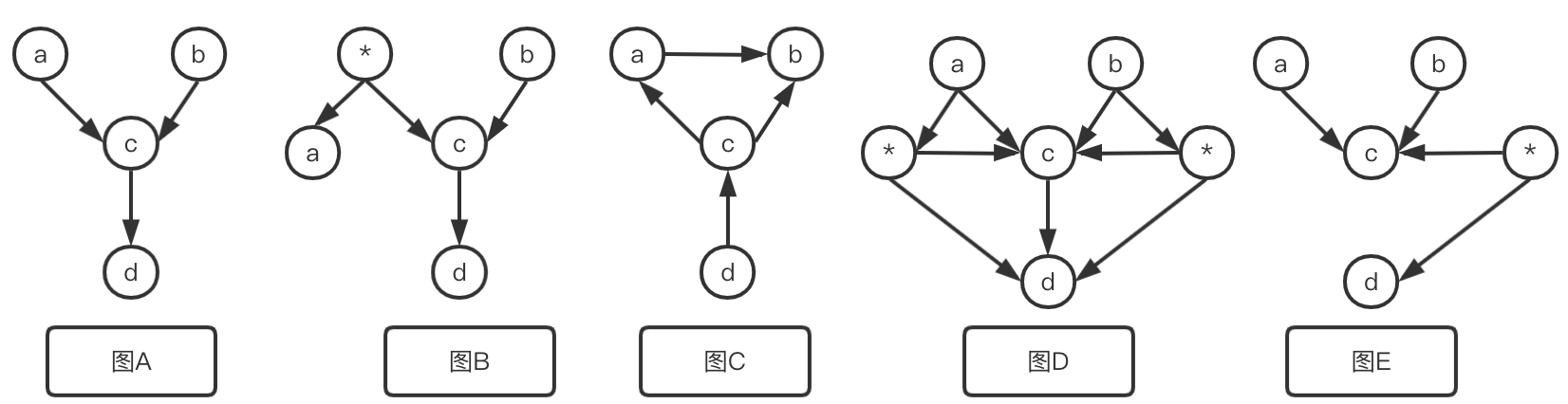
上图中的* 表示隐藏原因。可以看到图A和图B是符合极小性原则以及推断关系的c->d的合理因果结构。图C的结构容纳啦a和b的任意分布。 同样的图D也不是极小的,因为它未能强制的在c的条件下保证(a,b)⊥d,所以会容纳c条件下d与(a,b)的相关分布。在图E中,强行加入了(a,b)与d之间为观察到的边缘独立。上图想表达的关系就是a⊥b和d⊥(a,b)∣c
稳定分布
虽然极小性原则能够形成因果推断的规范理论,但它不能保证实际数据生成的模型结构是极小的,并且无法保证从一个极小结构的海量空间中进行搜索在计算上是可行的。想象这样一个case, A,B分别表示抛掷一枚硬币,其结果是相互独立,但是存在一个变量C,当AB结果相同的时候表示1,否则表示0. 然后咱们来看ABC这三个变量的关系,AB一对变量都是边缘独立的,但是在第三个变量的条件下确实相关的。这种依赖模式实际上可能是三个最小因果结果产生的,每个结构都把其中一个变量描述为因果上依赖另外两个变量,但是没有办法从结构中进行选择。这就是为什么要对分布施加一个稳定的限制。
令I(P)表示P中蕴含的所有条件独立关系集合,当且仅当P(D,θ)不包含额外的独立性,就是当且仅当对于任意的参数θ′,I(P(D,θ))∈I(P)(D,θ′),因果模型M=(D,θ)生成稳定的分布。
稳定性的条件表明,当我们将参数θ变化为θ′的时候,P中独立性均不会被破坏,因此称为稳定性。通过里一个例子来总结一下最小性和稳定性。
T1:图片中有一把椅子
T2:图片中有两把椅子,一把被另一把隐藏啦
对于极小性来讲,更加偏好T1,因为单个对象场景比多个对象更加简单,稳定性则先验的就排除T2,因为它认为两个对象不太可能对齐,且这样的对齐是不稳定的。
构建DAG结构
通过上面介绍的稳定性准则,只要没有隐藏的变量,每个分布都有唯一的极小因果结构。那么对极小结构的搜索可以归结为通过检索条件独立性来重构有向无环图的D的结构,并假定这些独立性反应了某些未知的、潜在的有向无环图D中的d分离条件。
IC算法
输入变量: 变量集合V上的稳定分布Pˉ
输出: 对Pˉ相容的模式H(Pˉ)
对于V中的每对变量a和b,寻找一个集合Sab使得(a⊥b∣Sab)在Pˉ中成立,构建无向图G使得当且仅当集合Sab不存在时,链接节点ab。
对于每对具有公共邻居c的非邻接变量a和b,检查c∈Sab是否成立
- 如果成立就继续
- 如果不成立,就添加指向c的有向边(a->c<-b)
在得到的部分有向图中,根据以下两个条件尽可能多的无向边定方向。
- 任意可选的方向会产生一个新的v结构
- 任意可选的方向会产生一个有向环。
在线性高斯模型中,通过求逆矩阵的协方差矩阵的非0项对应的变量对赋予边的方法。这也是求解概率图的一种方法。
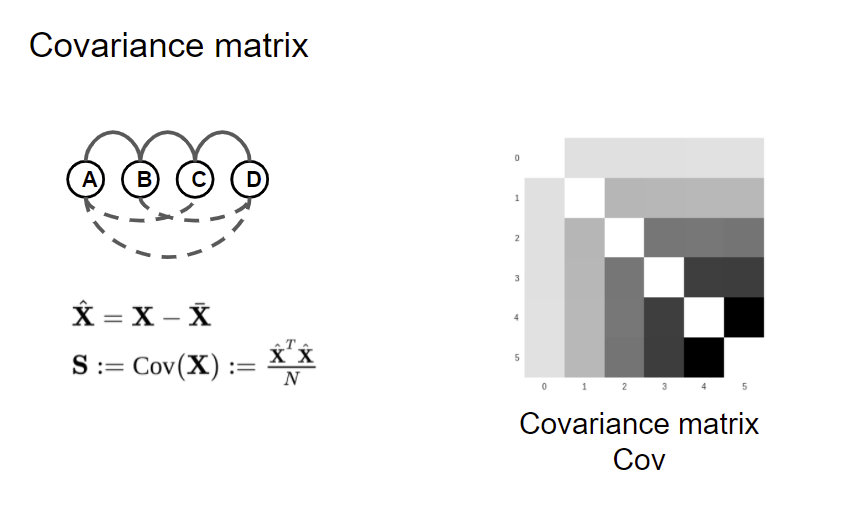
求上图的协方差矩阵。对上面的协方差矩阵求逆,就直接得到了概率图的结构。
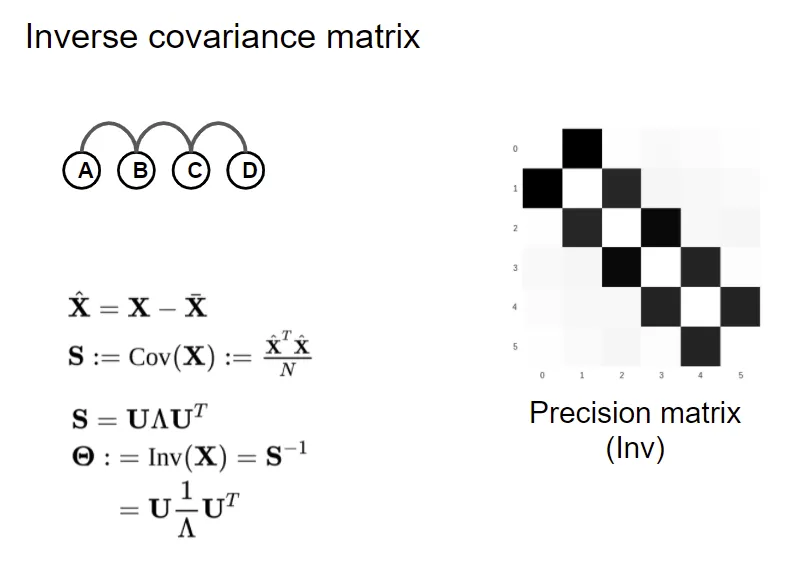
这里你可能会有一个疑问,是不是直接使用协方差矩阵就行了。其实直接使用协方差矩阵显示出的信息是粗糙的。与协方差矩阵的逆矩阵相比,发现协方差矩阵与协方差矩阵求逆之间有一定的关系,这两个矩阵表达的信息是一样的。所以往往可以通过协方差矩阵求逆来消除两个随机变量之间的间接耦合。
对于上的算法步骤存在一些历史的解法,从变量0到Sab集合开始,一旦发现分离,就从完全图中递归的删除相应的边,称为PC算法。这种算法在节点度有限的图中是多项式时间的复杂度,因为每个阶段,对分离的Sab的搜索可以限制a和b的邻接节点上。IC算法精炼了以下4个规则。
- 如果存在a->b使得ac不邻接,就将b-c定向为b->c.
- 如果存在a->c->b,就将a-b定向为a->b
- 如果存在a-c->b和a-d->b使得c和d不邻接,就将a-b定向为a->b
- . 如果存在a-c->d和c-d->b使得c和d不邻接而a和d邻接,就将a-b定向为a->b.
重建潜在结构
潜在结构LO=(DO,O), 其中D是极小结构,O是观测集合。是另一个潜在结构L的投影,当且仅当
- DO中每个未观测变量都恰好是两个非相邻的可观测变量的共同原因,且该变量无父代变量
- 对于L生成每个稳定的分布P,都存在一个LO生成的稳定结构P’,使的I(PO)=I(PO′)
这里一般使用IC* 算法进行求解,IC* 不对边进行定向,而是对边的顶点添加箭头,从而容许双向边。
下面介绍潜在原因的定义,如果下面的条件成立,则认为条件X和条件Y有潜在的因果影响。
- X和Y在每种情形下都相关
- 存在变量Z和情形S使得, a.给定S的条件下,X和Z独立(X⊥Z∣S) (b)给定S的条件下,Z和Y相关.
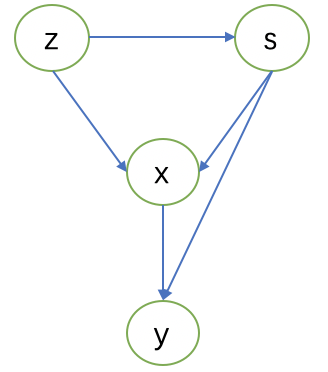
这里的情形指的是变量赋予固定的值。这里需要举个例子。如下图1结构,Z=c在情形S=a的情况下。c与b独立,因此变量b是d的潜在原因。
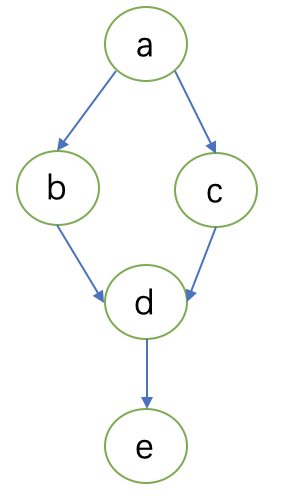
如果存在变量Z满足以下二者之一,则变量X对变量Y有真实的因果影响
- X和Y在任何情形下均相关,且存在情形S满足
- Z是X的潜在原因
- 给定S,Z和Y相关
- 给定S∪X的时候,Z和Y独立
- X和Y在准则1定义的关系传递闭包中。
同上看上面的图1结构,X=d, Y=e, Z=b, S=NULL. 就能够按照上面的条件判断,d是e的真实原因。
当两个变量X和Y是虚假关联,如果他们在某些情形下相关,且存在另外两个变量Z1,Z2和两种情形S1,S2使得
- 给定S1, Z1和X相关
- 给定S1, Z1和Y独立
- 给定S2, Z2和Y相关
- 给定S2, Z2和X独立
条件1和条件2使用Z1和S1排除了Y作为X的原因,条件3和4使用Z2和S2排除X作为Y的原因。剩下唯一的解释就是存在潜在的共同原因导致X和Y之间观察到的关联性。如 Z1−>X−>Y<−Z2
具有时间信息的真实因果
变量X对Y有因果效应,如果存在第三个变量Z和情形S,二者都在X之前出现,且满足
- Z⊥Y∣S
- Z⊥Y∣S∪X
上面的定义与之前提到的真实原因定义是一致的,除了构建Z作为X的潜在原因的时候要求时间优先。
具有时间信息的虚假关联
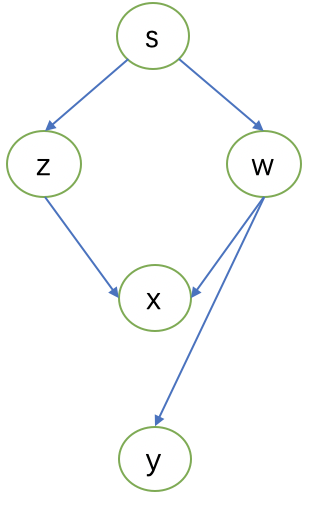
两个变量X和Y是虚假关联,如果在某些情形S下,X优先与Y,且满足
- Z⊥Y∣S
- Z⊥X∣S
总而言之
本文介绍了关于构建因果架构的一系列的定义和概念,都是围绕如何来定义目前网络中的关系,后续会尝试举一些生活中的例子补充进来,以方便大家理解。