学习了很长时间的因果知识，人们经常想通过因果关系的发现，尽可能的解答反事实的问题，那么什么是反事实呢？ 白话的表达是， 当你做了动作A以后，如果不做会有什么样的后果就是一种因果表达。例如“如果选择复读，是否能考上清华的问题？”

反事实

因果模型

我们先来介绍因果模型的一种形式化的定义。
因果模型是一个三元组的模型，$M=<U,V,F>$.

1. 其中U是一组背景变量（也称为外生变量），由模型外部因素决定。
2. V是有变量组成的集合，称为内生变量
3. F是函数的组合，每个$f_{i}$都是从$U_{i} \cup PA_{i}$到$V_{i}$的映射。 $v_{i}=f_{i}(pa_{i},u_{i})$

子模型

令M为一个因果模型，X为V中的一组变量集合，x是X的一个具体的赋值。M的子模型$M_{x}$的定义为

$$M_{x}=<U, V, F_{x}>$$

它的一个因果模型。
也就是说$F_{x}$通过删除F中与集合X的变量相应的所有函数，并且替代成x。

行为效应

令M为一个因果模型，X为V的一组变量集合，x是X的某一个具体得值。子模型$M_{x}$定义了行动do(X=x)对M的效应。

潜在响应

令X和Y为V上任意两个变量的子集合。Y对行为do(X=x)的潜在响应表示为$Y_{x}(u)$，是方程组$F_{x}$中Y的解，就是$Y_{x}(u)=Y_{M_{x}}(u)$

反事实

令X和Y为V上的两个变量的子集合。反事实语句“在条件u下，如果X取值x，则Y为y”。$Y_{x}(u)=y$,其中$Y_{x}(u)=y$为Y对X=x的潜在响应。

通过形式化的介绍完上面几个定义，咱们开始列举实际的例子，说明反事实到底是什么？

SEM表达反事实的例子

原始因果模型如下。

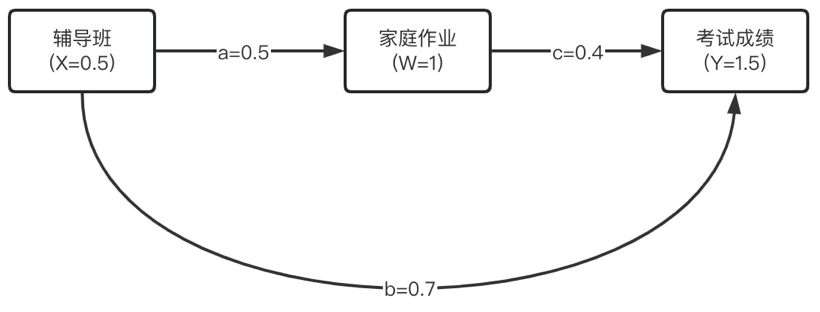
其中a,b,c都是通过大量数据拟合而来。并且学习了如下的关系

$$X=U_{x} \\ W=aX+U_{w} \\ Y=bX+cW+U_{y} \\$$

观测数据 X= 0.5, W=1, Y=1.5,推断如下

$$U_{x}=0.5 \\ U_{w}=1-0.5 * 0.5=0.75 \\ U_{y}=1.5-0.5*0.7-1*0.4=0.75$$

当我们将作业翻倍以后，成绩能提升多少？

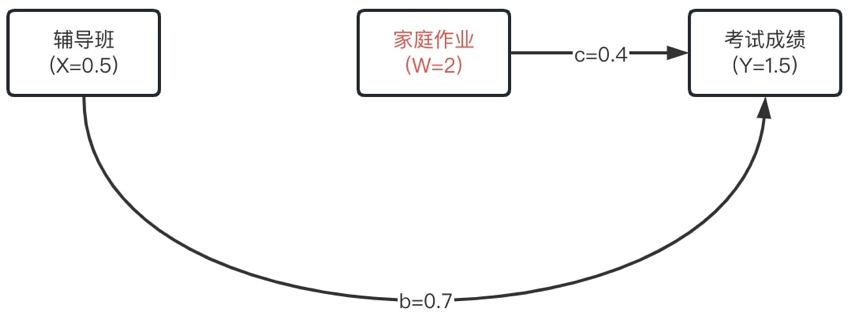
$$Y=0.5*0.7+2*0.4-0.75=1.90$$

也就是说如果翻倍作业，成绩能从1.5提升到1.9.

反事实得概率表达

概率因果模型是一个二元组

$$<M, P(u)>$$

其中M是因果模型，P(u)是定义在域U上的概率函数。
反事实语句的概率可以通过子模型$M_{x}$导出函数 $Y_{x}(u)$以相同的方式进行定义。

$$P(Y_{x}=y)=\sum_{(u|Y_{x}(u)=y)} P(u)$$

同样的，因果模型定义了反事实语句的联合分布，也就是说，对于变量X，Y，Z，W的任意集合，定义了$P(Y_{x}=y,Z_{w}=z)$。特别的对于$x \neq x', P(Y_{x}=y,X=x')$和$P(Y_{x}=y,Y_{x'}=y')$.

$$P(Y_{x}=y,X=x')=\sum_{(u|Y_{x}(u)=y\&X(u)=x')} P(u) \tag{1.1}$$

$$P(Y_{x}=y,Y_{x'}=y')=\sum_{(u|Y_{x}(u)=y\&Y_{x'}(u)=y')} P(u) \tag{1.2 }$$

通过上面的描述， 我们实际感兴趣的是，根据实际的观测变量来计算反事实的概率。例如“当事件X=x是事件Y=y的原因”的概率可以解释为，假设X=x并且Y=y真实发生啦，如若X不为x，那么Y不等于y的概率。通过上面的描述也就是说我们要获得$P(Y_{x}=y'|X=x, Y=y')$的表达。

$$P(Y_{x}=y'|X=x, Y=y')=\frac{P(Y_{x',X=x,Y=y})}{P(X=x,Y=y)} \\ =\sum_{u} P(Y_{x'}(u)=y')P(u|x,y)$$

也就是说首先需要更新P(u)从而得到P(u|x,y),然后使用更新后的分布P(u|x,y)计算$Y_{x'}(u)=y'$的期望。

推理反事实

已知模型<M, P(u)>，给定事实e的情况下，可以通过以下三个步骤评估反事实。”如果A发生，B会发生“的条件概率$P(B_{A}|e)$

1. 溯因，利用事实e更新P(u)得到(u|e)
2. 行动，通过行动do(A)修改M，获得子模型$M_{A}$，其中A是反事实的前提
3. 预测，通过修改后的模型<M_{A},P(u|e)>计算B的概率，就是反事实的结果。

概率因果图举例

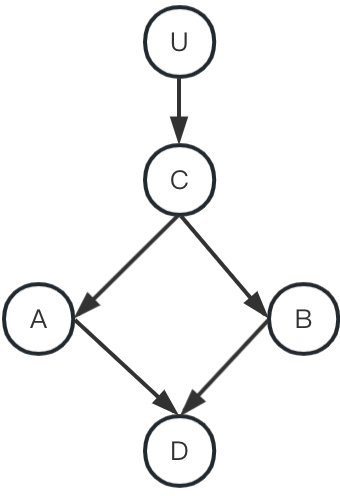
U=法院下令执行死刑
C=队长发出指令
A=行刑警察A开枪
B=行刑警察B开枪
D=囚犯死亡

1. 法院下令执行死刑的可能性P(u)=p
2. 行刑警察A因果紧张扣动扳机的概率为q
3. 行刑警察A的紧张与U无关

计算$P(\urcorner D_{\urcorner A}|D)$的概率，也就是已知囚犯死亡，如果A没有开枪，囚犯存活的概率是多少。
模型<M,P(u,w)>

$$C=U \\ A=C \vee W \\ B=C \\ D=A \vee B$$

那么背景变量分布为

\begin{equation} P(u,w)=\left\{ \begin{aligned} pq \ \ \ ,u=1,w=1\\ p(1-q) \ \ \ ,u=1,w=0\\ (1-p) q \ \ \ ,u=0,w=1\\ (1-p)(1-q)\ \ \ ,u=0,w=0 \end{aligned} \right. \end{equation}

溯因

溯因需要计算后验概率P(u,w|D)，因为发现囚犯已经死亡的事实，这就很容易得到。

\begin{equation} P(u,w|D)=\left\{ \begin{aligned} \frac{P(u,w)}{1-(1-p)(1-q)} \ \ \ ,u=1或w=1\\ 0 \ \ \ ,u=0,w=0 \end{aligned} \right. \end{equation}

行动

行动子模型$M_{\urcorner A}$, 形式化表达$<M_{\urcorner A},P(u,w|D)>$.

$$C=U\\ \urcorner A \\ B=C \\ D=A \vee B$$

预测

在上述概率模型中计算$P(\urcorner D)$, 其期望为

$$P(\urcorner D_{\urcorner A}|D)=\frac{q(1-p)}{1-(1-q)(1-p)}$$

总而言之

从上面的过程能看出，我们是能够通过概率的视角计算反事实结果的。当然实际的应用中计算P(u|e)的表达可能十分巨大，经常使用孪生网络的方法计算反事实的结果。