今天咱们进一步看因果推断的内容，做的业务多了以后你就发现，每当端到端的模型，一般不能解决你的认知问题，你做了一个端到端的模型，可能仅仅也就是是个模型，可能最重要的是你从这个事情中学到了什么？这个才能驱使你成为一个专家，行业专家。 所以多了解一些因果推断的内容是十分必要的，今天就来看看uplift建模方式。

重新出发

因果推断的建模大致为了解决以下几个问题。
ITE: 单体的处置效应

$$ITE=Y_{i}(T=1)-Y_{i}(T=0)$$

ATE: 平均处置效应

$$ATE=E[Y(T=1)-Y(T=0)]$$

CATE:条件处置效应

$$CATE=E[Y(T=1)-Y(T=0)|X=x]$$

这里咱们引入一个业务背景，假如我要研究一下给一个人发券还是不发券的区别，那就肯定不是一个ATE的问题。而是研究ITE，进一步的如果我们有各种场景，例如年龄大于30岁等等，就变成了CATE的问题。

uplift模型

这里介绍的一下uplift模型， 与uplift模型对应的是Response Model， Response Model是咱们经常机器学习用到的，根据各个特征之间的分布变化，模型给出反馈，例如预测用户看过广告之后转化的概率，不区分自然转化人群（即有些用户即使不用广告触达也会转化）；
而uplift模型就大有不同，预测用户因为广告而购买的概率，这是一个因果推断的问题，帮助我们定向营销敏感人群，预知每个用户的营销敏感程度，从而制定差异化营销策略，促成整个营销的效用最大化。进而咱们通过营销的四个象限来看这个问题。

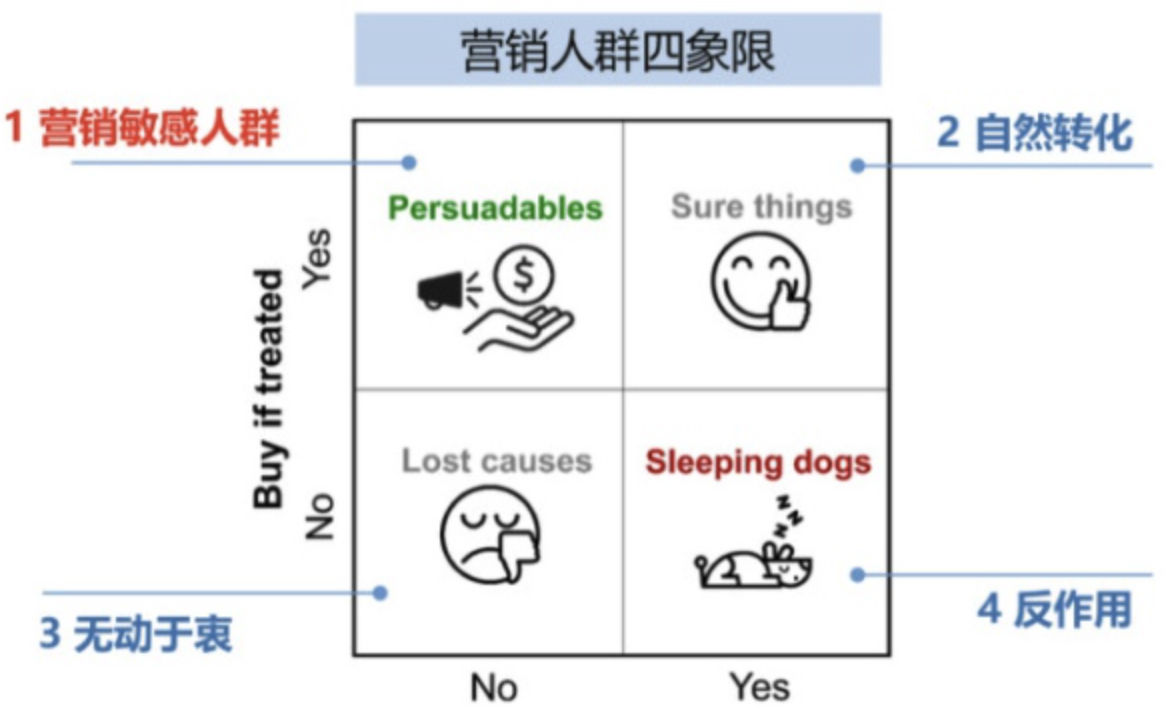
Persuadables：不发送优惠券则不买，发送优惠券则购买；
Sure things：不论是否发送优惠券均会购买；
Lost causes: 不论是否发送优惠券均不会购买；
Sleeping Dogs: 不发送优惠券会购买，发送优惠券反而不买

这个时候，根据上面的四个象限，发现对于Sure things和Lost causes这类用户的发券行为价值是不大的，反而是对于Persuadables这类用户的发券是必要的，那么怎么找到这些用户呢？ 主要方式通过AB实验的方式，获取处置和非处置的数据，进行建模，通过判断用户I，对于发券不发券的行为进行一个减法操作，获取当前这个用户是否是一个Persuadables。

1. response模型的目标是估计用户看过广告之后转化的概率，但是我们没有办法从中区分出自然转化人群。
2. uplift模型则是估计用户因为广告而购买的概率，这是一个因果推断的问题，帮助我们锁定对营销敏感的人群。
   所以不要再用response模型去解决这类问题啦，可能你把手里的钱全发到Sure things这部分人手里了，对于业务的影响很小，代价却很大。

建模方式

元模型

差分响应模型 Two-Learner Method

最简单的思路是对A组和B组数据进行单独建模,我们对实验组(有干预)和对照组(无干预)的购买行为进行分别建模，然后用训练所得两个模型分别对全量用户的购买行为进行预测，此时一个样本用户即可得出有干预和无干预情况下两个购买行为预测值。这两个预测值的差就是我们想要的uplift score。这种建模方法较简单且易于理解，可以复用常见的机器学习模型(LR、Tree Model、NN)。

$$\mu_{0}(x)=E(Y(0)|X=x) \\ \mu_{1}(x)=E(Y(1)|X=x) \\ t(x)=\hat{ \mu_{0}(x)}-\hat{ \mu_{1}(x)} \tag{1.1}$$

缺点

1. 对照组和实验组分别建模，两个模型完全隔离，可能两个模型各有偏差从而导致预测的误差较大。其次建模的目标是Response而不直接是Uplift，因此模型对Uplift的预测能力较有限；
2. 策略只能是离散值，不能是连续变量，因为有几种策略就需要建几个模型。所以当干预条件只有‘是否发优惠券’时，此建模方法可行，但是当涉及到‘多种优惠券面额/文案组合策略’或者‘发多大面额优惠券这种连续变量策略’时，本种建模方法可能并不非常work；

差分响应模型升级版 Single-Learner Method

Single-Learner在Two-Learner的基础上，将对照组数据和实验组数据放在一起建模，使用一个模型对处理效果进行估计，然后计算该样本用户进入实验组和对照组模型预测的差异作为对实验影响的估计。与Two-Learner不同的是，本模型将实验分组（干预项）作为一个单独特征和其他变量一起放入模型中对用户购买行为进行建模，干预项可以是多种组合策略或者连续变量。

$$\hat{\mu(x,w)}=E[Y|X=x, W=w] \\ t(x)=\hat{\mu}(x,1)-\hat{\mu}(x,0) \tag{1.2}$$

优点

1. 模型训练时数据利用更充分.
2. 建模更加简单，只需要一个简单的逻辑回归或树模型(随机森林、Xgboost、Lightgbm).
3. 能对处理变量或者其他变量进行强制的单调约束，双模型无法做到这一点.

缺点

1. 同时和Two Model版本类似，它的缺点依然是其在本质上还是在对response建模，因此对uplift的建模还是比较间接，有一定提升的空间。
2. 对随机实验数据要求较高，否则容易造成偏差.
3. Treatment影响容易被其他特征淹没。

标签转换模型 Class Transformation Method

这种方法是最好的刻画处置效应的方法，相对于上面的one model方法，希望通过数据层进行打通，一个用户既有可能被发券，又有可能被不发券，分别看着这两种情况下对于同一个用户的影响，更解决真实的处置效应。针对这样的数据建模，整个结果的提升会很明显。

S-learner

这个模型最简单，直接把Treatment作为特征放进模型来预测，将处置动作放到模型里当特征，通过学习模型权重，对于实际应用时候，改变处置的真值，判断相减之后的就是处置效应估计。

$$ITE=Y(x=1)-Y(x=0) \tag{1.3}$$

这里有一个问题就是，当你修改处置特征的时候，是否真正的影响模型的结果，如果你有1000维度，仅仅修正了1维，结果改变的幅度很小，就很难估计出处置效效应，那么应该尽可能的使用简单模型的直观特征，效果才能有所保证。

X-learner

S-learner和T-learner都非常依赖数据集的样本数目，如果实验组和对照组的样本数量非常不平衡，比如实验组的样本数量非常少，那么拟合出来的base learner的准确性就会非常差。
为了解决这个问题，X-learner在拟合base learner时会使用实验对照两组的信息。

1. 分别建立response模型

$$\mu_{0}(x)=E(Y(0)|X=x) \\ \mu_{1}(x)=E(Y(1)|X=x) \tag{1.4}$$

2. 计算实际产出和预估产出之间的差，得到填充疗效(imputed treatment effect)：

$$\hat{D_{i}^{0}}=\mu_{1}(x_{i})-Y_{i}^{F} \\ \hat{D_{i}^{1}}=Y_{i}^{F} - \mu_{0}(x_{i}) \\$$

3. 使用$x_{0}$作为特征（未处置），$\hat{D_{i}^{0}}$ 作为标签在对照组训练模型$\hat{t_{0}}(x)$, 使用$x_{1}$作为特征，$\hat{D_{i}^{1}}$ 作为标签在实验组训练参数模型$\hat{t_{1}}(x)$.
4. 计算CATE，$t(x)=g(x)\hat{t_{0}}(x)-(1-g(x))\hat{t_{1}}(x)$。

uplift评估(AUUC)

$$f=(\frac{Y_{t}}{N_{t}}-\frac{Y_{c}}{N_{c}})\times(N_{t}+N_{c})$$

$Y_{t}$:实验组中的积极响应数量（positive responses in treatment group）
$N_{t}$:实验组的样本数量（number of samples in treatment group）
下标c表示对照组。
$(\frac{Y_{t}}{N_{t}}-\frac{Y_{c}}{N_{c}})$表示实验组和对照组中的积极响应比例之间的差异。
实验组和对照组的划分方式是按照score排序后，不同的分位数下的实验组和对照组

公式想表达的意思是评分越高的
通过观察以上指标， 10分位数的f和20分位数的f，越好的模型应该是f10大于f20，并且下降越快。
AUUC的计算方式十分简单，使用模型会有一个预测的值，像AUC一样，横坐标是x%是当成实验组，1-x%当成对照组，然后计算平均score的差，就是纵坐标的值。