本章主要讲解一下在连续特征值的情况下如何进行因果图的挖掘。之前的介绍中节点的属性大部分以是否值为主。
之前讲的优化的框架是如下的公式表达。
$$\begin{gather}max\ F(A) \\
s.t.G(A) \in DAGs \tag{1.1}\end{gather}$$
F(A)表示图的打分， A 为因果结构的邻接矩阵,G(A)为A 所对应的有向无环图，DAGS 是所有可能的DAG组成的离散空间.公式1.1能够在低维做一个优化，并且取得比较好的结果，但是本身公式1.1是一个非凸的优化问题，无法直接求解。为解决这个问题，学者们提出了一种连续优化方法口: 基于迹指数和增广拉格朗日的非组合优化结构学习( Non-combinatorial Optimization via TraceExponential and Augmented lagRangian for Structure learning，NOTEARS)。该方法采用数值解法，将 DAG 学习问题转化为约束的数值优化问题，下面我们将介绍该方法。
模型构造
假设数据 $D \in R^{n \times N}$包含 n 个独立同分布的观测样本，其中每个观测样本由N个变量组成，即 $V\{V_{1},..,V_{N}\}$,而数据对应的总体分布为 P(V)。结构学习的任务是从所有结构中找出服从数据分布 P(V)的结构。 连续优化方法引入结构等式模型 ( Structural Equation ModelSEM)的概念，以描述变量之间的关联及相互作用。形式上，SEM 由两个部分变量组成:
$$
V_{j}=A_{j}^{T}V_{-j} + U_{j} \tag{2.1}
$$
$V_{-j}$表示节点集合中除去$V_{j}$的所有节点，$U_{j}$表示偏置。至于这个表示方式一般使用权重邻接矩阵的方式，也就是$A_{ij}$表示邻接矩阵A中，i节点和j节点之间的权重。通过矩阵的表达， 简化了计算的方式。
$$
V_{j}=A_{j}^{T}V + U_{j} \tag{2.2}
$$
这里的V表示为矩阵的除了$V_{j}$以外的行向量，而$A_{j}^{T}$表示权重。很明显这里有一个可优化的方程。
$$
l(A,D)=|\frac{1}{2n}(D-DA)|^{2} \tag{2.3}
$$
也就是真实值与其他的特征与权重的乘积的差别，这就是一种损失函数。其实就是最小二乘法的损失函数，如果将这个最小二乘法损失降低到最小，那么我们就获得了真实的因果结构。此外对于一个回归性问题，G的分布应该是稀疏的，要加入一个稀疏正则项，从而得到最后的损失函数为
$$
F(A)=l(A;D)+\lambda ||A||=\frac{1}{2n}|D-DA|^{2}+\lambda ||A|| \tag{2.4}
$$
这个时候优化方程就变成了如下的样子
$$\begin{gather}min\ F(A) \\
s.t. G(A) \in DAGs \tag{2.5}\end{gather}$$
很明显接下来就要解决的问题就是无环的约束问题啦， 怎么能通过量化的方式表达呢？
无环的约束方法
我们先来许愿， 希望这个无环的判断长成什么样子呢？ 我先来许愿
- 有一个函数h(A)=0，就表示无环，也就是h(A)越大也能表示环越多。
- 函数h的光滑的
- 导数是便于计算的
这里咱们直接给一个定理，如果$B= A \odot A$，A是权重矩阵，对应图的G位有向无环图，当且仅当$h(A)=tr(e^{B})-N=0$, 其中$\odot$表示哈达码积，$e^{B}$表示矩阵指数，tr表示矩阵的迹，并且有
$$
tr(e^{B})=tr(I)+tr(B)+tr(\frac{B^{2}}{2!})+tr(\frac{B^{3}}{3!}) \tag{2.6}
$$
可以进一步看上面这个公式2.6。tr(I)=N永远成立，也就是tr(B)=0才能保证上面的公式成立，这里有个小推论，矩阵中有长度为l的环必然有导致$B^{l}$的迹。
有了上面这个定理。公式2.5进一步可落地啦。
$$\begin{gather}min\ F(A) \\
s.t. h(A)=0 \tag{2.7}\end{gather}$$
上面这个运筹方程的求解可以使用增广拉格朗日方法进行求解，使用对偶函数近似最优解。但是这一些都是基于线性的假设。
增广拉格朗日方法在原损失函数F(A)的基础上添加上h(A)的二次惩罚项，$\rho$表示惩罚系数，转化为如下的问题
$$\begin{gather}Dual(\alpha)=min_{A \in R^{N \times N}}L^{\rho}(A,\alpha) \\
L^{\rho}(A,\alpha) = F(A)+\frac{\rho}{2} |h(A)|^{2}+\alpha h(A) \tag{2.8}\end{gather}$$
神经网络进行DAG学习
如果变量之间存在非线性关系，显然这是一个基础假设的崩塌，那么如何解决非线性的问题呢？
第一反应应该是神经网络类的方法，是的，神经网络在结构复杂到一定程度下能拟合任何的函数形式。那我们新的范式表达也十分简单。
$$
V_{j}=MLP_{j}(V_{-j}, \theta) \tag{2.9}
$$
这里需要注意一下，我们实际上是为每个$V_{j}$都有一个神经网络。也就是我们有多个MLP。整体结构如下图所示。
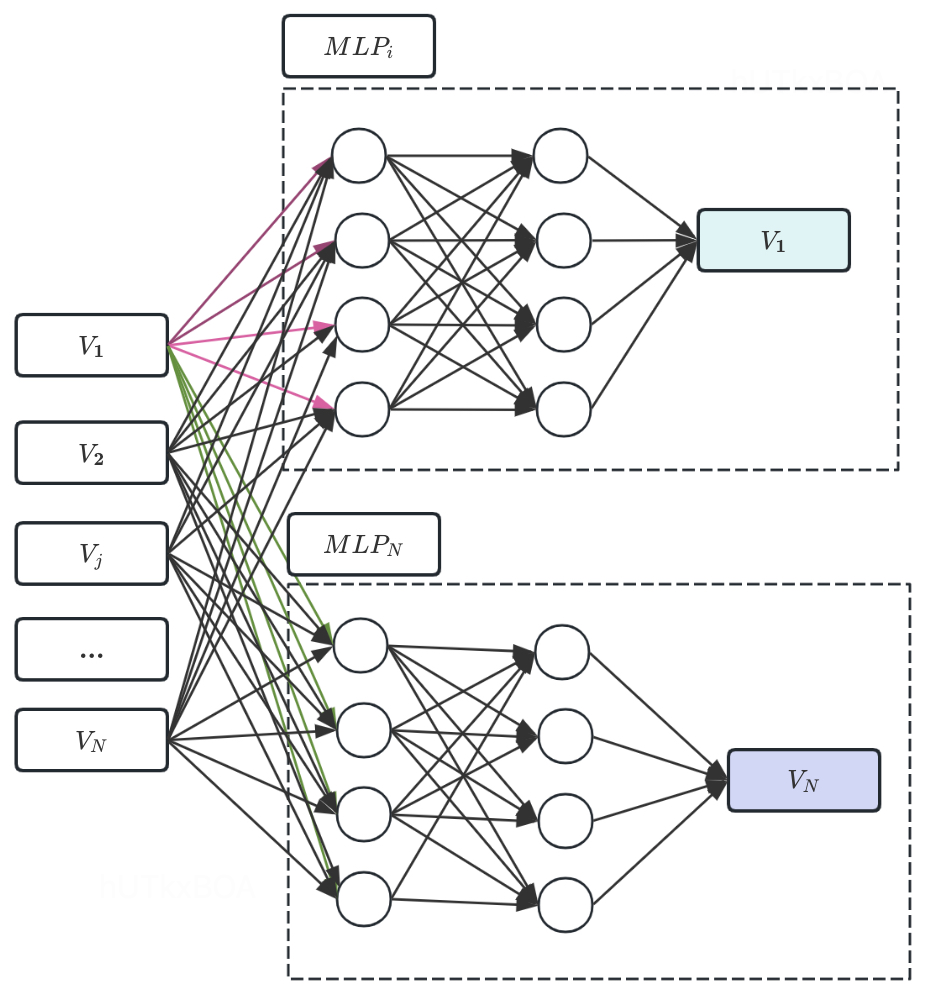
邻接矩阵表达
这里还要解决一个问题，有了神经网络网络的协助，最后图的结构还是需要一个邻接矩阵的表达，已经融入和神经网络中的参数，怎么表达邻接矩阵的关系呢？可以试想一些神经网络的传播过程，如果$MLP_{j}$表示$V_{j}$变量的生成网络， 如果参数的矩阵的第k列都是0，表达什么含义呢？说明$V_{k}$这个变量无法传递到下一层，是不是说明$V_{j}$和$V_{k}$是独立的，且没有边关系。这里公式2.8就可以通过神经网路的方式进行表示。
$$
min_{\theta} (\frac{1}{n} \sum_{j}^{N}(l(V_{j},MLP_{j}(V_{-j},\theta_{j}))+\lambda|W_{j}|)+\frac{\rho}{2}|h(A(\theta))|^{2}+\alpha|h(A(\theta))|) \tag{2.10}
$$
进一步给迭代的规则
$$\begin{gathered}\theta^{k}=argmin L_{\rho^{k}}(\theta,\alpha^{k}) \\
\alpha^{k+1}=\alpha^{k}+\rho^{k} h(A^{k}) \\
\rho^{k+1}=\eta \rho^{k}\ if|h(A^{k})|>\gamma |h(A^{k-1})| \\
\rho^{k+1}=\rho^{k}\end{gathered}$$
可见F(A)可以通过神经网络拟合，通过神经网路的学习，从生成模型中提取出邻接矩阵，在进行阈值的筛选就可以得到对应的有向无环图。
DAG-GNN
之前的方式是通过MLP当时学习DAG，接下来的这一个章节学习的是通过GNN学习权重邻接矩阵，并将DAG的学习问题转化为无环约束的数字优化问题。
问题转化
首先还是使用结构等式框架（SEM）为基础，回顾线性表达,D为数据样本矩阵，U是噪声矩阵，A是邻接矩阵。
$$
D=A^{T}D+U \tag{3.1}
$$
$$\begin{gathered}D-A^{T}D=U \\
D(I-A^{T})=U\\\end{gathered}$$
为了得到D，对上式取逆是因为 𝐴是一个严格上三角矩阵，保证了 $(I-A^{T})$的特征值都不为零,我们可以两边同时乘以$(I-A^{T})^{-1}$
$$
D = U(I-A^{T})^{-1}U
$$
当时数据对应的变量中所有的变量按照拓扑排序的方式，这权重矩阵A是一个严格上三角矩阵
$$
D=(I-A^{T})^{-1} U \tag{3.2}
$$
进一步可以表示为$D=f_{A}(U)$，以U为输入，返回D为输出的图神经网络的形式
$$
D=f_{2}((I-A^{T})^{-1} f_{1}(U) ) \tag{3.3}
$$
公式3.3中，$f_{1},f_{2}$表示参数函数，可以分别对D和U进行线性和非线性转换。公式3.3可以看做是一个解码器，学习DAG的任务变成了优化D的生成模型和学习权重邻接矩阵A的问题。
这个时候如果给定样本D和U的分布形式（高斯分布但是均值和方差未知），希望通过公式3.3得到D的生成模型，并通过优化生成模型得到邻接矩阵A。这个时候可以通过最大似然的方式求得D的分布形式。 也就是最大化log p(D),也就是最大化D的概率。因为还有U的参数，所以是最大化如下的公式表达。
$$
\frac{1}{n} \sum_{k=1}^{n}log p(D^{k})=\frac{1}{n}\sum_{k=1}^{n} \int p(D^{k}|U)p(U) dU \tag{3.4}
$$
这个时候发现上面的公式很难计算，这个可以采用变分编码器（VAE）的方式拟合生成机制，进而获得一个接近真实分布的变分后验。
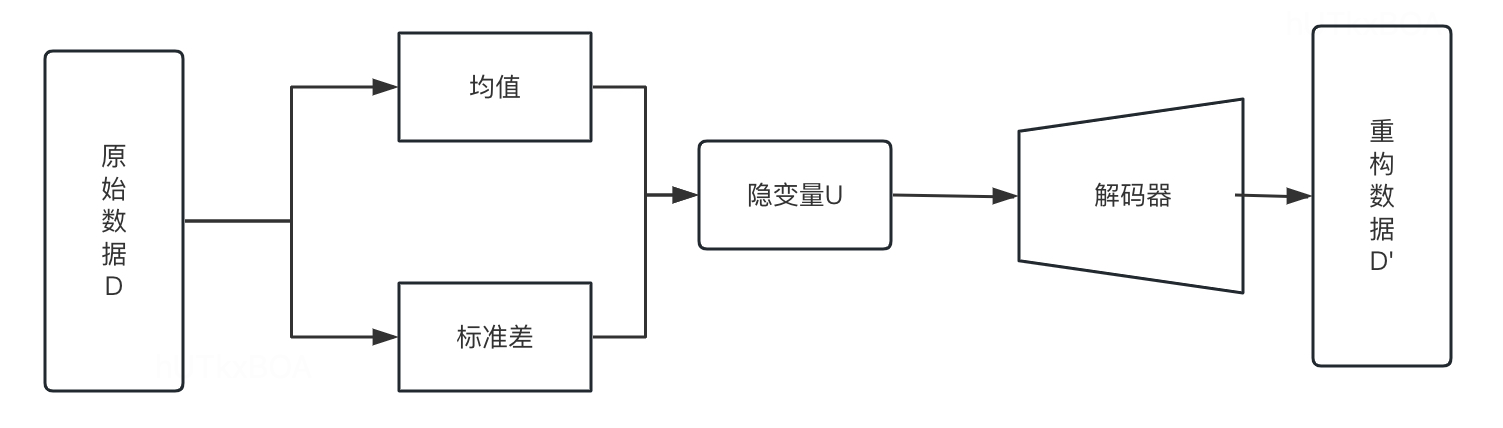
如上图所示，变分解码器将输入的数据用解码器压缩到低维空间，其做法是将原始数据D经过编码器得到因变量U的分布所需的各项元素，得到因变量U，然后得到重构数据D‘。
在使用VAE的时候，给定一个样本$D^{k}$,编码器将其编码成$q(U|D^{k})$的隐变量U，然后经过解码器从U从重构出来$p(D^{k}|U)$的$D^{k}$，则编码器表示为如下形式(对应公式3.3)
$$
U=f_{4}((I-A^{T})f_{3}(D)) \tag{3.5}
$$
解码器表示为
$$
D=f_{2}((I-A^{T})^{-1}f_{1}(D)) \tag{3.6}
$$
令$f_{3}$为MLP，而$f_{4}$表示恒等映射，$f_{2}$为MLP，$f_{1}$表示恒等映射，如下图所示
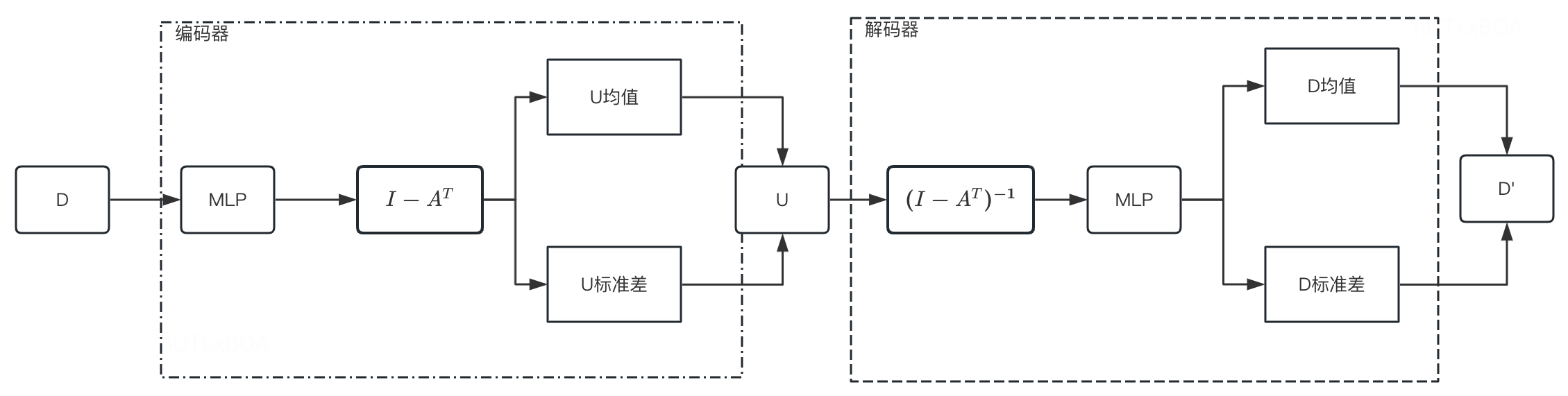
上图的神经网络可以形式化如下的方式
$$\begin{gathered}[U均值|U标准差]=(I-A^{T}) MLP(D,W_{1},W_{2}) \\
MLP(D,W_{1},W_{2})=relu(DW_{1})W_{2} \\
[D均值|D标准差]=MLP((I-A^{T})^{-1}U, W_{3},W_{4})\end{gathered}$$
这里还需进一步进入一个无环约束定理，
令$A \in R^{N \times N}$为一个有向图对应的邻接矩阵，对任意的$\alpha>0$，该有向无环图当且仅当如下的条件成立
$$
tr[(I+\alpha A \circ A)^{N}]-N=0 \tag{3.7}
$$
从而根据重构损失和无环约束就可以表示为如下的表达式
$$\begin{gather}min_{A,\theta}\ f(A, \theta) \\
s.t. h(A)=tr[(I+\alpha A \circ A)^{N}]-N=0 \tag{3.8}\end{gather}$$
问题中未知的包括邻接矩阵A，$\theta=[W_{1},W_{2},W_{3},W_{4}]$,进一步使用增广矩阵的方式
$$
L(A,\theta)=f(A,\theta)+\alpha h(A)+\frac{\rho}{2} |h(A)|^{2} \tag{3.9}
$$
类似的更新公式
$$\begin{gather}(A^{k}, \theta)=argmin L(A,\theta) \\
\alpha^{k+1}=\alpha^{k}+\rho^{k} h(A^{k}) \\
\rho^{k+1}=\eta \rho^{k}\ if|h(A^{k})|>\gamma|h(A^{k-1})| \\
\rho^{k+1}=\rho^{k} \tag{3.10}\end{gather}$$
优化完成后就可以得到权重矩阵A和相应的有向无环图。因为使用神经网络重构数据切显示的定义了邻接矩阵，所以此处就要更新矩阵权重，又要更新神经网络参数。
总而言之
上面介绍了一些新的方法进行DAG的学习，当然还有些方式也能起到类似的学习下效果，例如基于对抗网络的因果结构学习SAM，如果感兴趣可以查阅相关的资料。