今天来讲一种更深的CNN网络,VGG神经网络。
更深的网络:VGG神经网络
VGG在卷积核方向最大的改进是将卷积核全部更换成了3×3,1×1的卷积核,而性能最好的VGG-16和VGG-19是由仅仅3×3的卷积核构成,这样做的原因主要有以下几个方面
- 根据感受野的计算方式rfsize=(out−1)×stride×ksize,其中stride是模型的步长,ksize是卷积核大小。我们知道一个7×7的卷积核和3层3×3的卷积核具有相同的感受野,由于3层的感受野具有更深的深度,因此可以构建出更具有判别性的函数。
- 假设特征图的数量是C,3层3×3的卷积核的参数数量是3×(3×3+1)×C=30C,但是7×7的卷积核的参数数量是1×(7×7+1)×C=50C, 参数量更大。
VGG家族
VGG-A(11层),VGG-B(13层),VGG-D(16层),VGG-E(19层)的错误率随着网络的深度增加,分类的错误率是逐渐降低的,当然深度也意味着训练时间越来越长,但是当深度达到VGG-D以后,网络的错误率开始收敛,这就是网络退化的问题。
VGG-B 和VGG-C
VGG-C在VGG-B的基础上添加了3个 1×1卷积核。而1×1卷积核主要的作用如下。
- 实现特征图的升维和降维
- 实现特征图之间的交互。
VGG-C 和VGG-D
VGG-D将VGG-C中的 1×1卷积核换成了 3×3卷积核,当然也证明了 3×3卷积核的提升效果是优于 1×1卷积核的。
VGG-C 和VGG-E
当网络增加到16层的时候,网络损失函数收敛,当提升到19层的时候,虽然精度有些提升,但是需要训练时间大幅度增加。
更宽的神经网络: GoogleNet
我了了解GoogleNet, 咱们先了解一下可以拟合任何凸函数的maxout网络和可以拟合任意函数的MIN网络结果。
Maxout网络
Maxout是深度学习网络中的一层网络,就像池化层、卷积层一样等,我们可以把maxout 看成是网络的激活函数层。
这里可以先介绍一下dropout操作,首先假设一层神经网络中有n个神经元,其输出为一个神经元。加上dropout后,有n×p个神经元失活,未加dropout前,其理想输出为z的话,那么经过dropout后这层神经元的输出期望就变成了(1−p)×z=(1−p)z,由前文可知,dropout相当于求多个神经网络的平均值,那么一个网络的输出值就为(1-p)z。我们需要保证这个网络在训练和测试阶段的输出基本不变即求网络的平均值。那么就有两种方式来解决:
第一种在训练的时候,让这个网络的输出缩放1/(1-p)倍,那么它的输出期望就变成(1-p)z/(1-p)=z,和不dropout的输出期望一致;
第二种方式是在测试的时候,让神经元的输出缩放(1-p)倍,那么它的输出期望就变成了(1-p)z,和训练时的期望是一致的。
这里引出Maxout网络, 与其使用dropout这种方式进行选择, 不如有条件的选择节点来生成网络。如果第i个隐层的计算方式为
hi=wxi+b
假设第i-1层和第i层的节点分别是d和m,那么w是d×m的二维矩阵。而Maxout网络中W是三维矩阵,d×m×k,其中k表示网络中的通道数。
hi=maxj∈[1,k]zi,jzi,j=xWi,j+bi,j
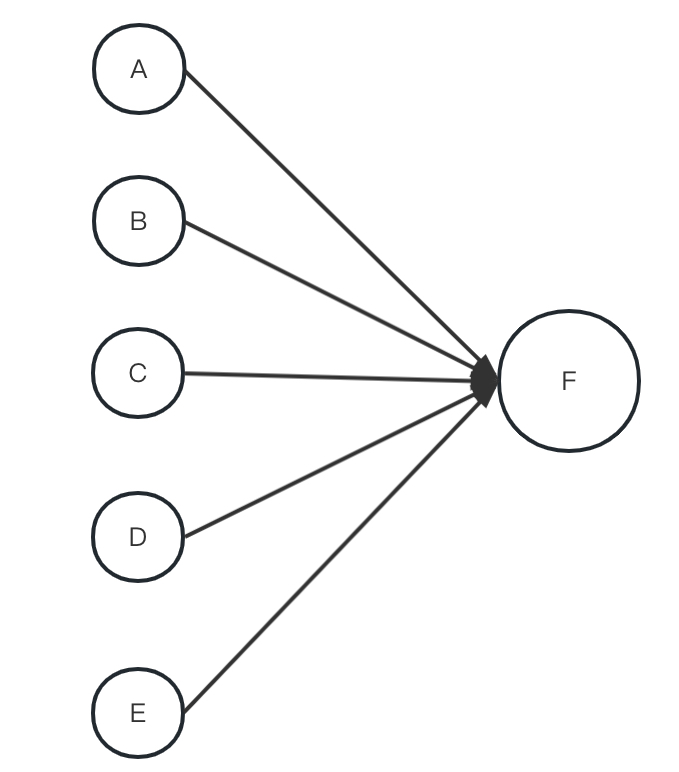
下面一个图来看看如果i-1层有两个神经元,i层有1个神经元的例子。
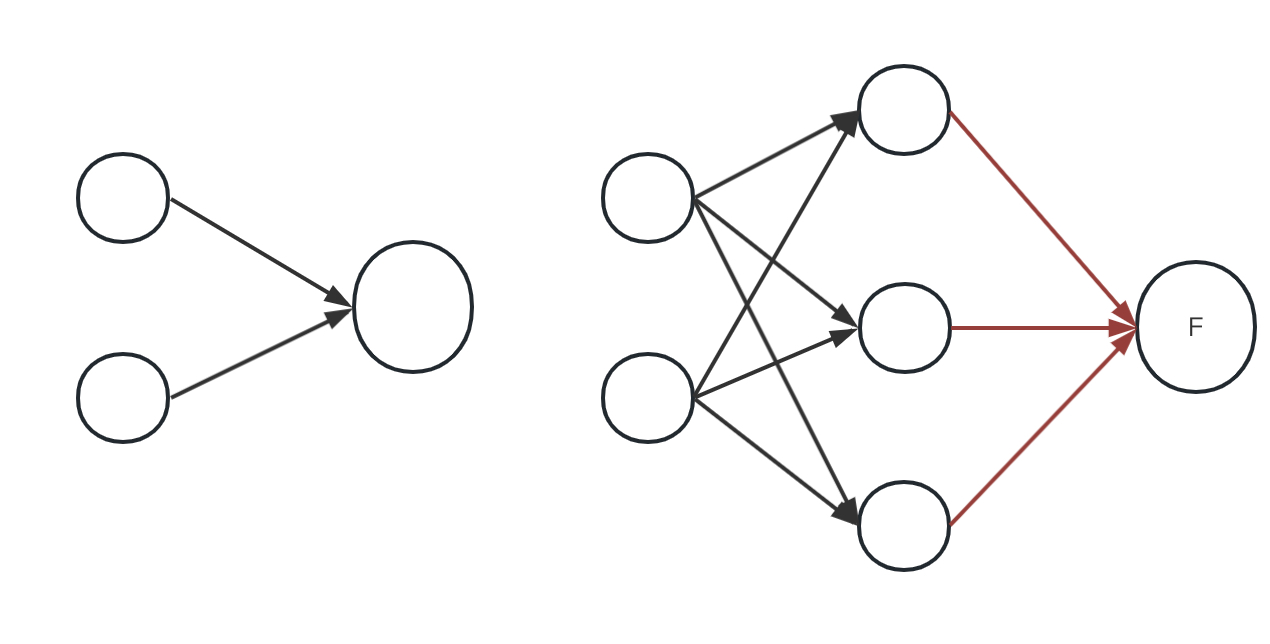
就是一个k=3的maxout网络, 其中红线是求max操作。
maxout网络存在一个比较大的问题是参数的数量是传统神经网的k倍,而这个参数的规模提升并没有带来相应的精度提升。
MIN网络
maxout网络可以逼近任何的凸函数,而MIN网络理论上能够逼近任何函数,MIN网络中采用整图滑窗的形式,只是将CNN卷积核替换成了一个小型的MLP网络。如下图
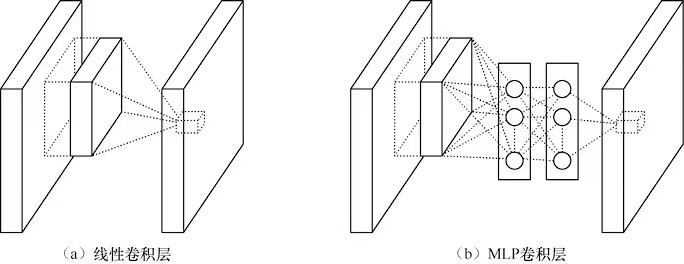
在卷积操作中,一次卷积操作仅仅相当于卷积核和滑动窗口的一次卷积乘法,其拟合能力有限。而使用MLP替代以后卷积操作增加了每次滑动窗口的拟合能力。同时也带来了如下的优点。
- MIN参数数量远大于同类型的CNN
- MIN的收敛速度快于经典网络
- MIN的训练速度慢于经典网络。
此外,MIN网络使用了平均池化来减轻全链接层的过拟合问题,就是在卷积的最后一层直接对每个特征图求均值,然后执行softmax操作。
Inception
GoogleNet的核心模块叫做Inception。
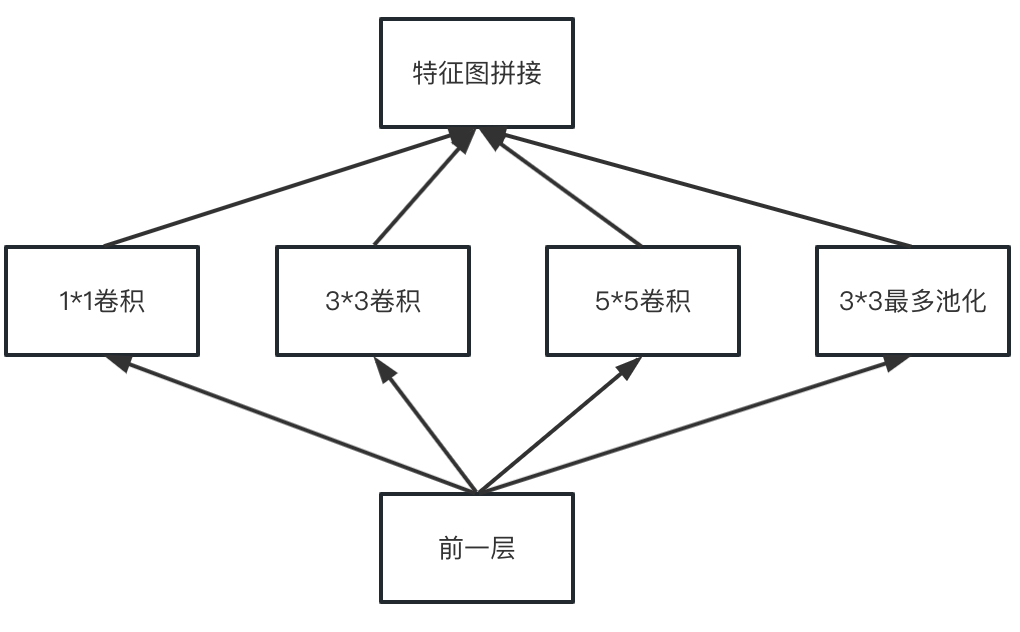
上面这个结构会使得参数量急剧增大,为了提升计算速度,Inception引入了MIN中1×1卷积核在卷积操作之前进行降采样,实际的结构如下。
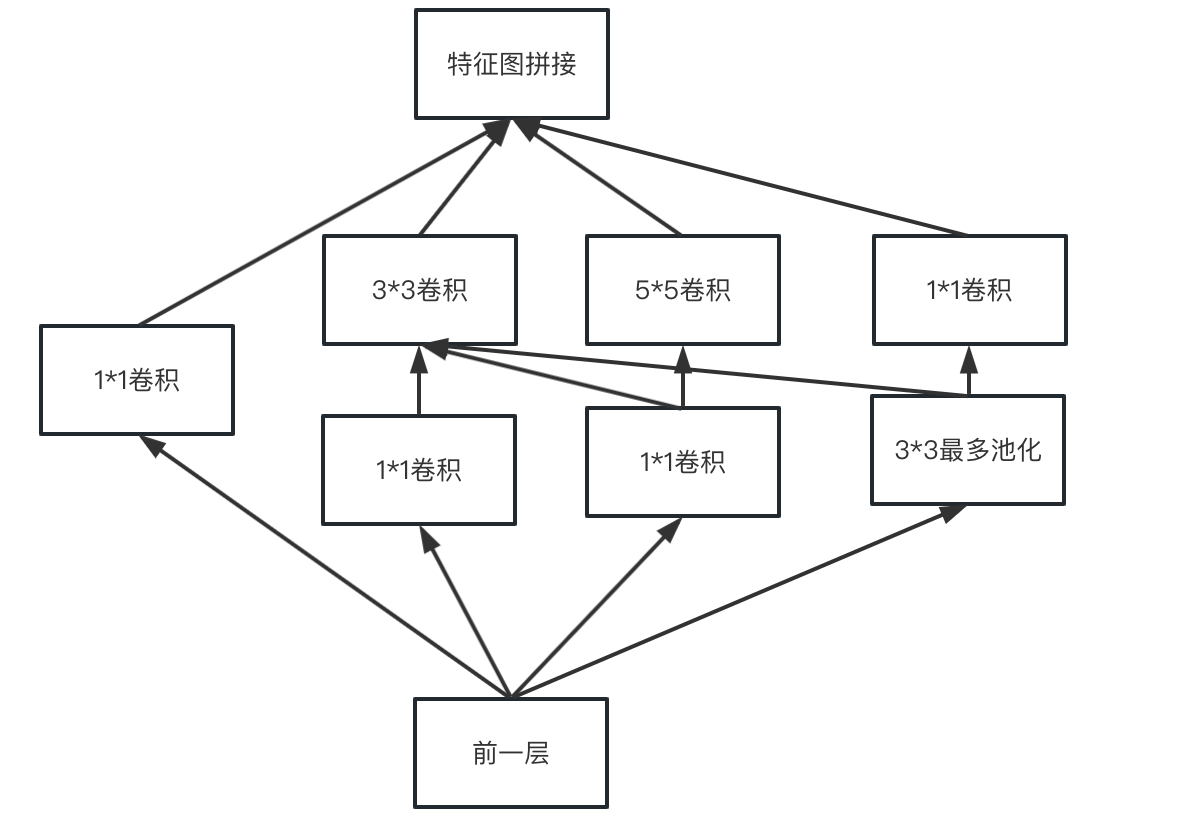
GoogleNet就是使用了Inception这样的模块进行组装,最大深度有22层。Inception当然也有一序列的变体,例如把5×5 变成更深的3×3卷积等操作这里就不详细做介绍啦。
Inception的参数量巨大, 所以更深的网络也更加容易带来过拟合等风险, 所有Inception 也会和残差网络进行结合,变成Inception-ResNet网络结构。下面会单独介绍一个残差网络的结构。
ResNet残差网络
ResNet残差网络诞生的背景是当网络深度过深的情况下, 模型容易过拟合,产生梯度爆炸或者梯度消失等问题。其实还伴随一个问题是,随着网络的加深,网络会有退化的现象,也就是说深层的网络效果可能不如浅层的网络。这个时候就产生了残差网络。
残差块
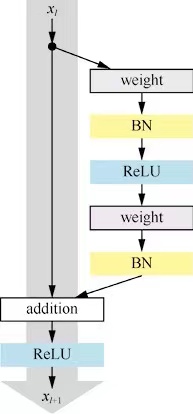
残差块分为两个部分,直接映射块和残差部分。其中weight在CNN中指的是卷积操作,addition指的是加操作。
xl+1=hxl+F(xl,Wl)
其中hxl是直接映射块, F(xl,Wl)是残差部分。有的时候xl+1和xl的特征图数量不太一样,一般用1×1卷积核进行升维和降维。
总而言之
接近尾声,总结一下,今天主要介绍了几个图形领域的网络,也是算是开山网络类型,以及中间遇到了一些问题,然后通过探索提出解决问题的模块,希望对大家有些帮助。