本文主要讲解使用梯度下降算法迭代熟悉的MSE损失函数。
J(θ)=E[(y−θTx)2]=σy2−2θTp+θTϕθ
MSE可以看上面这个博文了解上面这个公式。
其中ϕ是输入特征的协方差矩阵,p是输入和输出的互相关矩阵。
▽J(θ)=2ϕθ−2p(1.1)
其迭代过程如下公式
θ(i)=θ(i−1)−μ(ϕθ(i−1)−p)=θ(i−1)+μ(p−ϕθ(i−1))(1.2)
其中μ表示步长。
步长的收敛性
c(i)=θ(i)−θ∗θ∗ϕ=p
上面的公式1.2两边同时减去θ∗,得到如下公式
θ(i)−θ∗=θ(i−1)+μ(p−ϕθ(i−1))−θ∗c(i)=c(i−1)+μ(p−ϕc(i−1)−ϕθ∗)=c(i−1)−μϕc(i−1)=(I−μϕ)c(i−1)(2.1)
因为ϕ是正定的,所以有ϕ=Q∧QT,其中∧表示特征值,Q表示特征向量。将上面的条件带入公式2.1.
c(i)=Q(I−μ∧)QTc(i−1)(2.2)
进一步简化,v(i)=(I−μ∧)v(i−1),得到下面的表达式
v(i)=QTc(i)(2.3)
以上的转换是为了拆解公式1.2中的θ(i)的各个分量。v(i)(j)表示v(i)的第j个分量,且迭代路径和其他分量无关,满足以下表达式。
v(i)(j)=(1−μλj)v(i−1)(j)=(1−μλj)2v(i−2)(j)=(1−μλj)iv(0)(j)(2.4)
其中v(0)(j)是初始化的分量,如有以下的表达式成立。
∣1−μλj∣<1(2.5)
那么相应的次幂将趋近于0.,且
v(i)→0,QT(θi−θ∗)→0,逼近最优参数
那么这个时候,步长收敛的条件就是(公式2.5)
0<μ<λmax2
迭代速度
既然能保证保证迭代收敛,那么这个值的指定和迭代速度有什么关系呢?咱们继续来探索。
假设迭代的函数为f(t)=exp(τj−t),就是v, 将t=iT和t=(i-1)T带入到公式2.4中的v(i),v(i−1) ,求得是时间常数。
τj=ln(1−μλj)−1
如果两个迭代步之间采样的时间T=1,那么对于很小的μ,就有
τj=μλj−1(3.1)
通过这个公式能够知道,最慢的收敛速度与对应的最小特征值有关,不过这只是适用于μ比较小的情况。当然实际上是取决于1−μλj这一项决定,也称为第j个模态。
为了获取最佳的步长,必须以最小化得到最大模态绝对值的方式选择步长。
μ0=arg minμjmax∣1−μλj∣(3.2)
当然这个在下图中很容易被找到。求得的交叉点为。
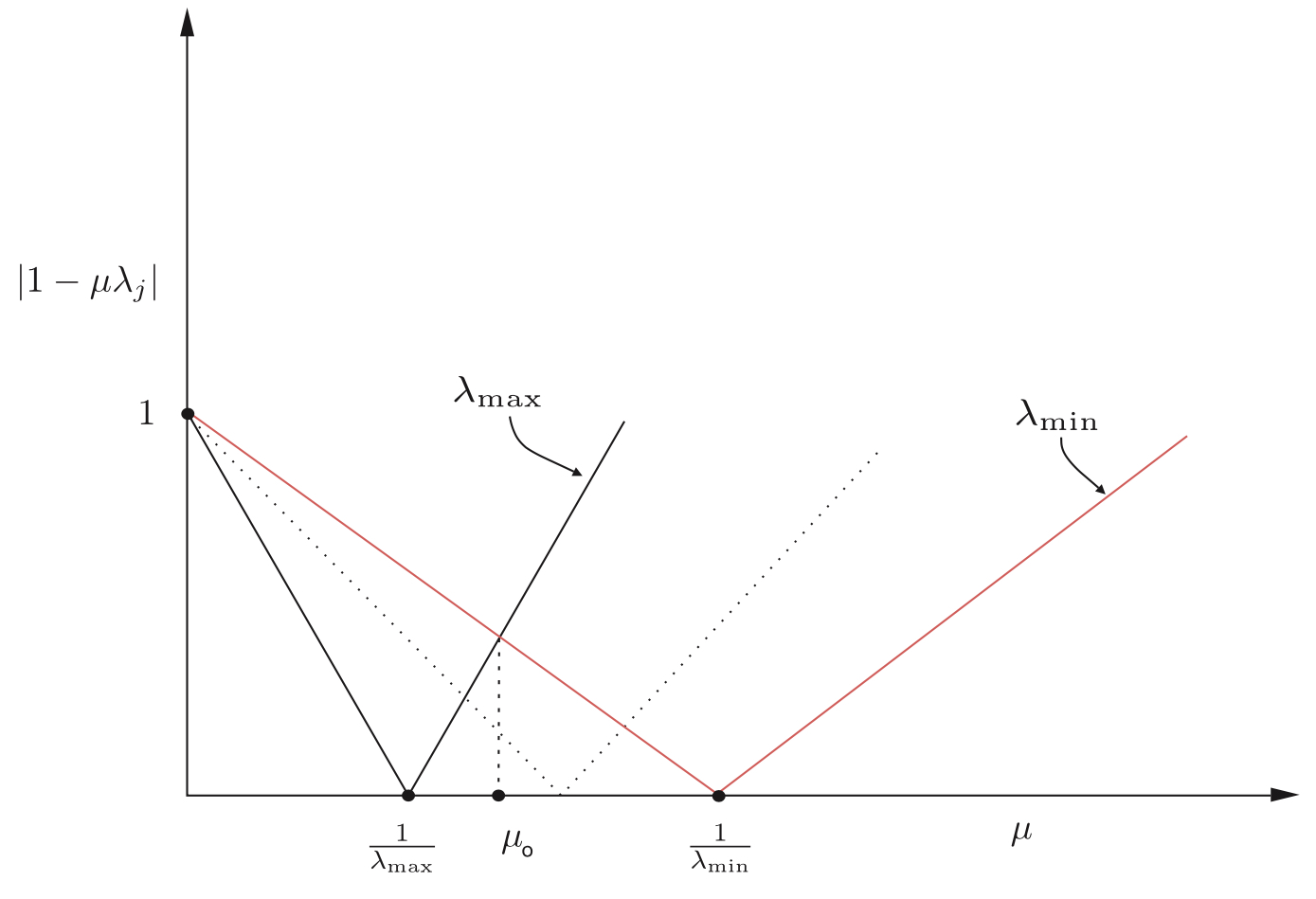
1−μ0λmin=−(1−μ0λmax)μ0=λmin+λmax2(3.3)
在最优处的μ0。有两个最慢的模态,一个对应于λmin,另一个对应于λmax就是1−μ0λmax,且大小相同,符号相反,这里只要公式3.3带入到1−μ0λi即可,就有如下的表达。
p+1p−1p=λminλmax
也就是说,收敛速度取决于协方差矩阵的特征值的扩散度。