图神经网络的发展经历了几个阶段，也体现了研究工作者在研究工作上精益求精的态度，接下来咱们一起看看这个发展历程。
基于谱分解的方法
基于谱分解的方式是2014年提出的，Spectral Network在傅里叶中定义了卷积的运算。该运算可以被定义为信号x（每个节点对应该向量中的一个标量）和一个卷积核$g_{\theta}=diag(\theta)$的乘积
$$
g_{\theta} \star x=U g_{\theta} (\wedge) U^{T}x \tag{1.1}
$$
其中U是归一化的拉普拉斯矩阵的特征向量组成的矩阵，$L=I_{N}-D^{\frac{1}{2}}AD^{-\frac{1}{2}}=U \wedge U^{T}$.这里的D是度矩阵，A是邻接矩阵，$\wedge$是特征值的对角阵。
这种卷积方式会导致潜在的密集的计算，并且导致卷积核不满足局部性(聚合节点和实际的空间结构不对应)等问题。
ChebNet
2011年的时候，David提出可以用切雪比夫多项式的前K阶T(x)逼近$g_{\theta}(\wedge)$
$$
g_{\theta} \star x \approx \sum_{k=0}^{K} \theta_{k}T_{k}(\bar{L})x
$$
其中$\bar{L}=\frac{2}{\lambda_{max}}L-I_{N}$。$\lambda_{max}$是L的最大特征值。$\theta \in R^{K}$表示切雪比夫多项式系数向量。$T_{k}(x)=2xT_{k-1}(x)-T_{k-2}(x)$，其中第0项是1.第1项是x。 这里的K就是图中的K阶局部化。从而省去了计算拉普拉斯矩阵特征向量的过程。
GCN
GCN在之前的章节中已经讲过了，这里就不详细讲了。需要补充的是GCN是在ChebNet的基础上将层级运算限制为K，从而缓解模型在节点度分布范围较大的图上存在局部结构的过拟合问题。不仅如此还假定了$\lambda_{max} \approx 2$
$$
g_{\theta} \star x \approx \theta_{0}'x+\theta_{1}'(L-I_{N})x=\theta_{0}'x-\theta_{1}' D^{\frac{1}{2}}AD^{-\frac{1}{2}}x \tag{3.1}
$$
并进一步简化为
$$
g_{\theta} \star x \approx \theta[I_{N}+ D^{\frac{1}{2}}AD^{-\frac{1}{2}}]x \tag{3.2}
$$
注意节点上迭代执行这一运算可能导致数值的不稳定以及梯度爆炸或者梯度消失的问题。为了解决这个问题 引入了重归一化的方法。
$$
[I_{N}+ D^{\frac{1}{2}}AD^{-\frac{1}{2}}]=\bar{D}^{\frac{1}{2}} \bar{A}\bar{D}^{\frac{1}{2}}
$$
其中$\bar{A}=A+I_{N}, \bar{D}_{ij}=\sum A{ij}$.
拉普拉斯算子
在介绍更多的神经网络之前，咱们先来介绍一下拉普拉斯算子的基础知识，对于一个三元的函数，其拉普拉斯算子的定义为f(x, y, z)
$$
\Delta f=\frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}} \tag{1.1}
$$
很多时候只能近似的计算导数值，然后回过来来看使用极限的方式理解。
$$
f'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x} \tag{1.2}
$$
对于f(x)的二阶导数如下
$$
f''(x)=\frac{f(x+\Delta x)+f(x-\Delta x)-2f(x)}{(\Delta x)^{2}} \tag{1.3}
$$
进一步延伸到多元的情况
$$\begin{gathered}\Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} \\
=\frac{f(x+\Delta x, y))+f(x-\Delta x, y))-2f(x, y)}{(\Delta x )^{2}}+\frac{f(x,\Delta y+y))+f(x, ,y-\Delta y))-2f(x, y)}{(\Delta y )^{2}}\end{gathered}$$
对上面的二元函数进行离散化，并进行采样能够得到下面这个矩阵, 下面这个矩阵只是一个例子，暂时构造一个3*3的矩阵
$$
\begin{bmatrix}
f(x_{1}, y_{1}) & f(x_{2}, y_{1}) & f(x_{3}, y_{1})\\
f(x_{1}, y_{2}) & f(x_{2}, y_{2}) & f(x_{3}, y_{2})\\
f(x_{1}, y_{3}) & f(x_{2}, y_{3}) & f(x_{3}, y_{3})
\end{bmatrix}
$$
这里x是水平方向，y是垂直方向，假设x和y的增量步长全是1，就是说
$$\begin{gathered}\Delta=x_{i+1}-x_{i}=1 \\
\Delta=y_{i+1}-y_{i}=1 \\\end{gathered}$$
点$(x_{i}, y_{i})$处的拉普拉斯算子可以通过下面公式近似推导
$$\begin{gathered}\frac{f(x_{i}+\Delta x, y))+f(x_{i}-\Delta x, y_{j}))-2f(x_{i}, y_{ij})}{(\Delta x )^{2}}+\frac{f(x_{i},\Delta y+y_{j}))+f(x_{i}, ,y_{j}-\Delta y))-2f(x_{i}, y_{j})}{(\Delta y )^{2}} \\
=f(x_{i+1},y_{j})+f(x_{i-1},y_{j})+f(x_{i},y_{j+1})+f(x_{i},y_{j-1})-4f(x_{i},y_{j})\end{gathered}$$
这个结果就是一个十分优雅的结果，它就是$(x_{i},y_{i})$的4个相邻点的函数值之和与$(x_{i},y_{i})$点处的函数乘以4的差值。
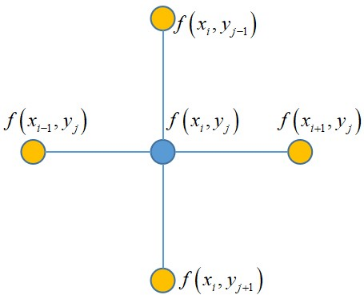
用上面这个图是不是十分好理解，这种形式经常也被用使用到图像的边缘检测的算法中。
拉普拉斯矩阵和图
这里咱们来介绍，这个拉普拉斯算子和拉普拉斯矩阵又是个啥关系，在前面二元函数的例子，一个点只是和上下左右四个邻居采样。那么如果推广到图上呢？如果将图的顶点处看做函数值，那么顶点i处的拉普拉斯算子就为
$$
\Delta f_{i}=\sum_{j \in N_{i}} w_{ij}(f_{i}-f_{j}) \tag{2.1}
$$
其中$N_{i}$表示顶点i的所有邻居集合，$w_{ij}$表示顶点间的权重，如果不是邻居关系，权重就为0。
$$\begin{gathered}\Delta f_{i}=\sum_{j \in V} w_{ij}(f_{i}-f_{j})\\
=\sum_{j \in V} w_{ij} f_{i} - \sum_{j \in V} w_{ij} f_{j} \\
=d_{i}f_{i}-w_{i}f\end{gathered}$$
这里$d_{i}$表示顶点i的加权度，$f_{i}$表示顶点值构成的列向量。这就能推导出拉普拉斯矩阵的计算形式
$$
L=D-W \tag{2.2}
$$
D是度矩阵， W是邻接矩阵
拉普拉斯矩阵的是特性
对于任意向量f，都有如下的等式关系成立
$$
f^{T} L f=\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij} (f_{i}-f_{j})^{2} \tag{3.1}
$$
- 拉普拉斯是半正定矩阵
- 拉普拉斯矩阵的最小特征值是0,且0的个数表示联通分量的个数。
- 拉普拉斯矩阵有n个非实数特征值，且满足
$$
0=\lambda_{1}<=\lambda_{2}<=..\lambda_{n}
$$
- 拉普拉斯矩阵的秩是N-K，K是拉普拉斯矩阵的联通分量，矩阵的秩表示一个矩阵的有效信息的维度。
- 对于任意的向量X，有如下关系
$$
X^{T} L(G) X= \sum_{i,j \in E} (x_{i}-x{j})^{2} \tag{3.2}
$$
L(G)是拉普拉斯矩阵。
举个例子
接下来咱们通过一个例子来看这个属性。
拉普拉斯矩阵的最小特征值是0,且0的个数表示联通分量的个数。
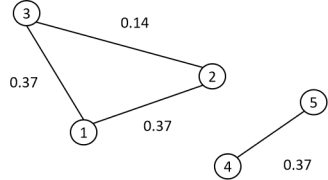
对于上面的图结构，是一个具有两个联通分量的结果，它的邻接矩阵如下。
度矩阵如下
拉普拉斯矩阵表示为
可以看出，上图图的拉普拉斯矩阵存在两个联通分量。 这在后面的图学习中能够保证，存在两个联通分量的图结果进行学习的时候，不会有权重进行传播。
拉普拉斯矩阵的形式
拉普拉斯矩阵一般使用会有几种常见的形式。
对称归一化
$$
L_{sym}=D^{-1/2}LD^{-1/2}=I-D^{1/2}WD^{1/2} \tag{4.1}
$$
随机漫步归一化
$$
L_{rw}=D^{-1}L=I-D^{-1}W \tag{4.2}
$$
归一化的性质
- 对于任意向量f都存在如下表达形式
$$
f^{T}L_{sym}f=\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij}[\frac{f_{i}}{\sqrt{d_{i}}}-\frac{f_{j}}{\sqrt{d_{j}}}]^{2} \tag{4.3}
$$
- $\lambda$是$L_{rw}$的特征值，$\mu$表示特征向量，当且仅当$\lambda$是$L_{sym}$的特征值且其特征向量为$w=D^{1/2} \mu$
- 0是$L_{rw}$特征值，其对应的特征向量为常量1， 0是$L_{sym}$的特征值，其对应的是特征向量$D^{1/2}1$