图神经网络(三)--GCN神经网络

今天我们来看一篇经典的论文，Semi-Supervised Classification with Graph Convolutional Networks,这个论文一个经典的讲gcn的论文。

我们经常遇到的卷积学习都是图上的卷积，具体形式可以在本站搜索『卷积神经网络』，我们发现卷积核都是方方正正的，就像为图片量身定做一样，那么我们生活中的的图一般不会用这么方方正正的图片来描述。例如我们人与人之间的关系网，知识图谱等内容不会用一个很大的图片来表示，这就是GCN的意义，GCN是支持我们在一个真正意义上的图进行卷积的，下面我们来看看上面这篇文章。

背景

在以往的文章中，大家是把图的拉普拉斯正则化放到损失函数中来解决图上的学习问题。

$$\zeta=\zeta_0+\lambda \zeta_{reg} \tag{1.1}$$

其中$\zeta_{reg}$,公式如下

$$\zeta_{reg} = \sum_{ij} A_{ij}||f(X_i)-f(X_j)||^2$$

$$= f(X)^T \bigtriangleup f(X)$$

可能有的人对上面的后半部分不理解，觉得怎么直接就相等了呢，这里我们可以看下拉普拉斯的矩阵性质。先来看那下面这个推导。

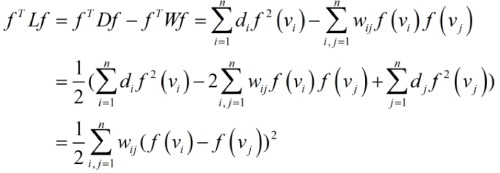
这样一来，拉普拉斯矩阵的意义就比较明显了，它是一种基于欧式距离的测度，如果$w_{ij}=1$,上式对应就是多个数据点的距离之和，同时也可以看出：D对应二次项，W对应不同一次项相乘。拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0

$\zeta_0$,就是普通的损失函数，而关键的$\zeta_{reg}$我们可以好好看一下，$f(.)$表示可以通使用神经网络转换的可微函数，$\lambda$是一个权重系数，$X$是节点的特征向量，$\bigtriangleup=D-A$，表示非规范化的拉普拉斯矩阵。$A$就是一个图的邻接矩阵，$D_{ii}=\sum_{j} A_{ij}$表示一个图的度矩阵。

我们可以理解一下$\zeta_{reg}$,先来看$\sum_{j} A_{ij}$，表示$i,j$节点的度矩阵，然后节点$i,j$节点经过函数$f$转换后做差，然后与我们的度矩阵相乘，也就是是这个公式中能够看出，这个公式成立的先决条件是，节点之间的相连，我们两个的标签就越一样，这个假设太严格了，极大限制模型能力，因为节点相连不一定都是相似，但会包含附加信息。

文章思想

GCN主流有两大类方法：

1. 基于空间的方法(spatial domain):将图数据规则化，这样就可以直接用CNN来处理了
2. 基于谱方法(spectral domain):利用谱图理论（spectral graph theory）直接处理图数据，本文是该类方法的代表作，简短介绍下相关的工作。

谱方法的理论基础，直接对图结构数据及节点特征进行卷积操作

我们定义卷积的过程是使用特征向量与卷积核$g_\theta$在傅立叶域上做乘法。

$$g_\theta \star x = U g_\theta U^T x \tag{1.2}$$

我们首先来看看矩阵分解的基础知识。

对于一个矩阵$A$，有一组特征向量；再将这组向量进行正交化单位化，也就是我们学过的Schmidt正交化，就能得到一组正交单位向量。特征值分解，就是将矩阵$A$分解为如下方式：

$$A=Q \sum Q^{-1} \tag{1.3}$$

这其中，$Q$是矩阵AA的特征向量组成的矩阵，$\sum$则是一个对角阵，对角线上的元素就是特征值。

是不是和我们上面的形式十分相近，那么我们来看下面的解释，

$U$是拉普拉斯矩阵$L = I_N - D^{-\frac{1}{2}} A D^{\frac{1}{2}}=U\Lambda U^T$的特征向量，$\Lambda$是由特征值组成的度矩阵，$U^TX$表示对图上的特征$x$的傅立叶变换，那么我们会发现，公式1.2中其实$g_\theta$是一个关于矩阵$A$的特征值的函数，看样子已经说的明白啦，但是有个问题，这个计算的复杂度可是不低，$O(n^2)$,所以我们需要简化这个计算。

推导简化

为了缓解计算问题，Hammond在2011年论文《Wavelets on graphs via spectral graph theory - HAL-Inria》 提出可以用切比雪夫多项式展开近似卷积核 $g_\theta$（类似泰勒展开）：

$$g_\theta(\Lambda)=\sum^{K}_{k=0}\theta_k'T_k(\vec{\Lambda}) \tag{1.4}$$

这里的$\vec{\Lambda}=\frac{2}{\lambda}\Lambda-I_N$,$\lambda$代表的是矩阵L的最大特征值，$\theta_k'$表示的是切比雪夫系数。$T_k$表示的是切比雪夫多项式,$T_k(x)=2xT_{k-1}-T_{k-2}(x)$.

很明显切比雪夫多项式是一个递归的形式，能够减少计算的成本。然后我重新来定义这个卷积$g_\theta$.

$$g_\theta \star x=\sum_{k=0}^{K}\theta_k'T_k(\vec{L})x \tag{1.5}$$

$\vec{L}=\frac{2}{\lambda}L-I_N$,卷积的k阶邻居的特征，$(U\Lambda U^T)^k=U\Lambda^kU^T$.

卷积核

上面是一堆理论，那么实际应用中我们是怎么使用这样的卷积呢？

使用切比雪夫一阶展开（K=1，线性）的卷积核，外套一个非线性单元。

$$H^{l+1}=\delta(\vec{D}^{-\frac{1}{2}} \vec{A}\vec{D}^{-\frac{1}{2}} H^t W^l) \tag{1.6}$$

$H^l$是上一层的输出，$H^0$是节点自身特征， $\vec{D}^{-\frac{1}{2}} \vec{A} \vec{D}^{-\frac{1}{2}} H^l$为一阶近似卷积核，可以简单理解成加权平均邻接特征。

1.增加自循环，$\vec{A}=A+I$,

2.对$\vec{A}$进行对称归一化，$\vec{A}=\vec{D}^{-\frac{1}{2}} \vec{A} \vec{D}^{-\frac{1}{2}}$，避免邻居数量越多，卷积后结果越大的情况以及考虑了邻居的度大小对卷积的影响。

$\delta$为非线性激活单元，如RELU，$w^l$为卷积层参数，每个节点共享该参数。

分层传播

每个卷积层仅处理一阶邻居特征，堆叠起来可以达到处理K阶内邻居特征。

这种作法一方面缓解当节点度分布非常广时的过拟合情况，另外也可以以更少的代价建立更深层的模型。

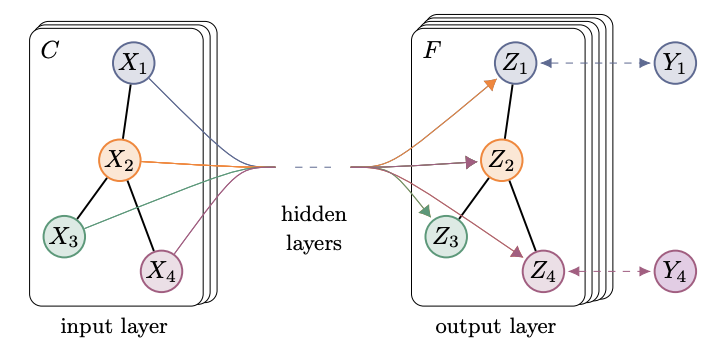
输入节点，$X_1,X_2,..,X_n$

经过卷积层的处理，最终输出F个分类对应的预测概率$Z_1,Z_2,..,Z_n$

其中$X_1$和$X_4$带标签，公共训练，最后给出所有节点的概率分布。

两层GCN

输入节点特征矩阵，$X\in R^{N \times C}$,以及邻接矩阵$A \in R^{N \times N}$

预处理邻接矩阵A：$\vec{D}^{-\frac{1}{2}} \vec{A} \vec{D}^{-\frac{1}{2}}$

第一层卷积+ 非线性变换, $H^0=RELU(\vec{A}XW)$

第二层卷积+softmax层。

$H^1=softmax(\vec{A}H^0W^1)$

实现复杂度为$O(|E|CHF)$ ，$C$为$X$的维度，$H$为中间层维度、$F$为输出层维度。

Semi-Supervised Classification with Graph Convolutional Networks