图表示学习
图结构是一个高维稀疏的数据表示,那么图表示学习是将这个高维稀疏的数据映射成低维度稠密的数据,这就是图表示学习的要解决的核心问题。图表示学习一般有两种方式,一种是顶点嵌入,另一种是整图学习。
顶点嵌入一般是针对顶点维度,将每个订单映射成一个低维的向量表达,这种方式表达的粒度比较细,一般用于节点层面的预测或者节点分类。
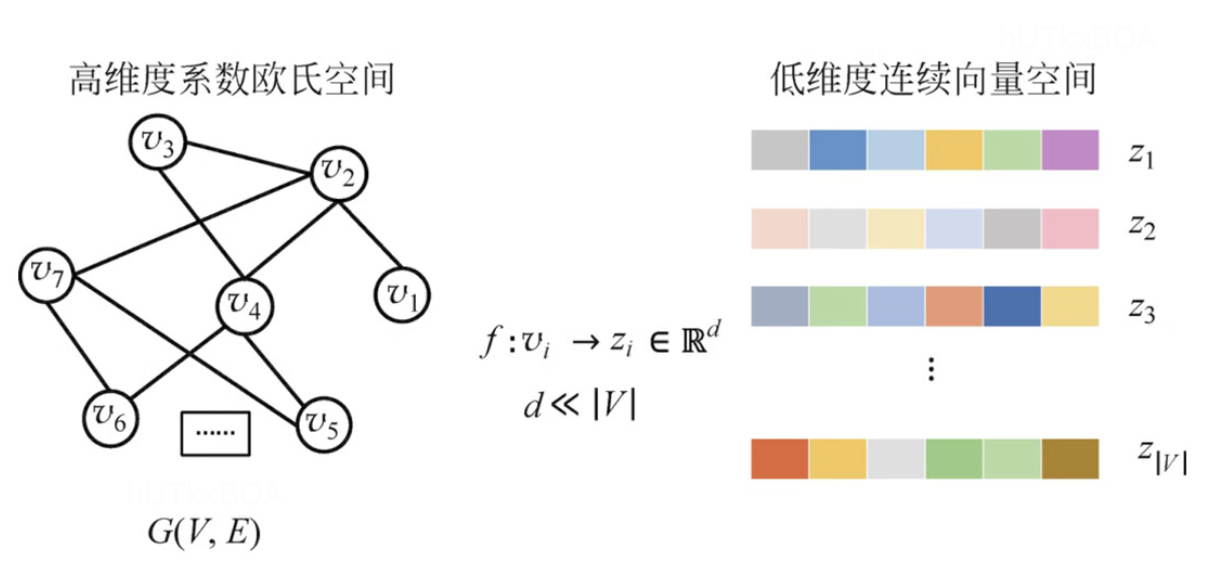
整图的表示学习则是针对全图生成一个向量,这种图表示学习方式粒度较粗,一般用于整图层面上的预测和比较的场景,几种基于图学习的分类。
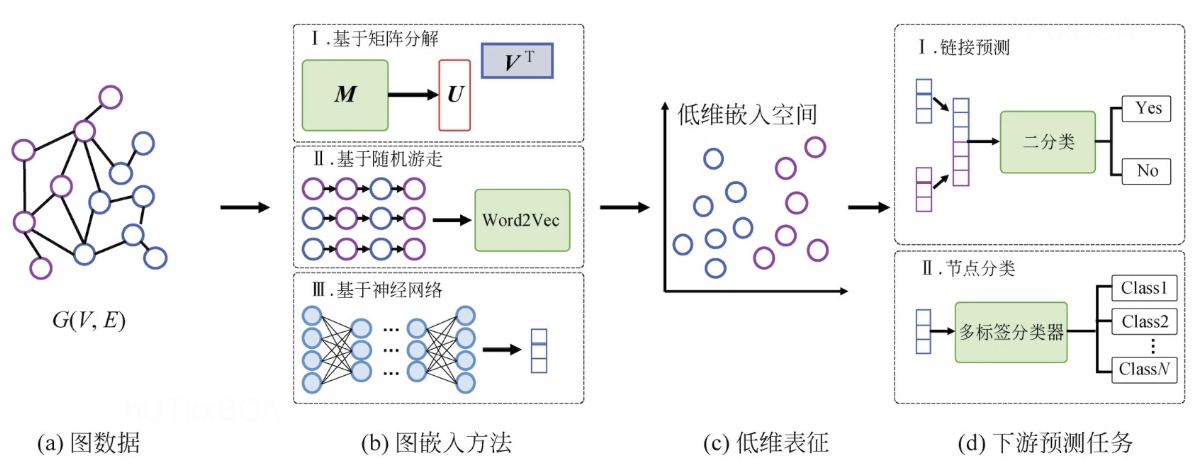
基于矩阵分解的图表示学习
图结构的矩阵表示通常包含邻接矩阵和拉普拉斯矩阵。基于矩阵分解的图表示学习通过矩阵分解获取图中的节点向量表征,接下来我们介绍拉普拉斯映射(LE)的方式进行图表示的算法。
LE算法算法的核心思想是希望相互有连接的点在降维空间以后尽可能的拉进,从而尽量使用低维的向量表示一个图结构的邻接关系。 根据我们的假设,我们期望一个好的降维操作是降维后的距离和降维前的相对关系尽可能保持一致。
mini∑j∑Wij∣yi−yj∣2(1.1)
其中∣yi−yj∣2表示目标空间空间内的两个数据点的距离, Wij表示两点之间的权重。公式1.1经过进一步的推导。
i∑j∑Wij∣yi−yj∣2=i∑j∑(yiTyi−2yiTyi+yiyiT)Wij=i∑(j∑Wij)yiTyi+j∑(i∑Wij)yiTyi−2i∑j∑yiTyiWij=2i∑DiiyiTyi−2i∑j∑yiyiTWij=2i∑(Diiyi)T(Diiyi)−2i∑yiT(j∑yiWij)=2trace(YTDY)−2i∑yiT(YW)i=2trace(YTDY)−2trace(YTWY)=2trace[YT(D−W)Y]=2trace(YTLY)
L就是拉普拉斯矩阵,但是为了找到使目标函数最小化的降维向量,同时又不让降维后的向量坍塌到过低的维度,故此设置了一个约束条件YTDY=1,例如yi=yj=0.
这样就把这个问题转化为一个广义的特征值的问题,就是求解如下的特征方程。
Lrwvi=λivi(1.2)
其中Lrw=D−1L=D{-1}(D-W)=I=DW. D是度矩阵,这样就得到降维后的结果啦。
Y=[v2,...vd+1]∈Rn×d(1.3)
LE算法的复杂度是节点数量的平方,所以算法不太适用于大规模图。
DeepWalk
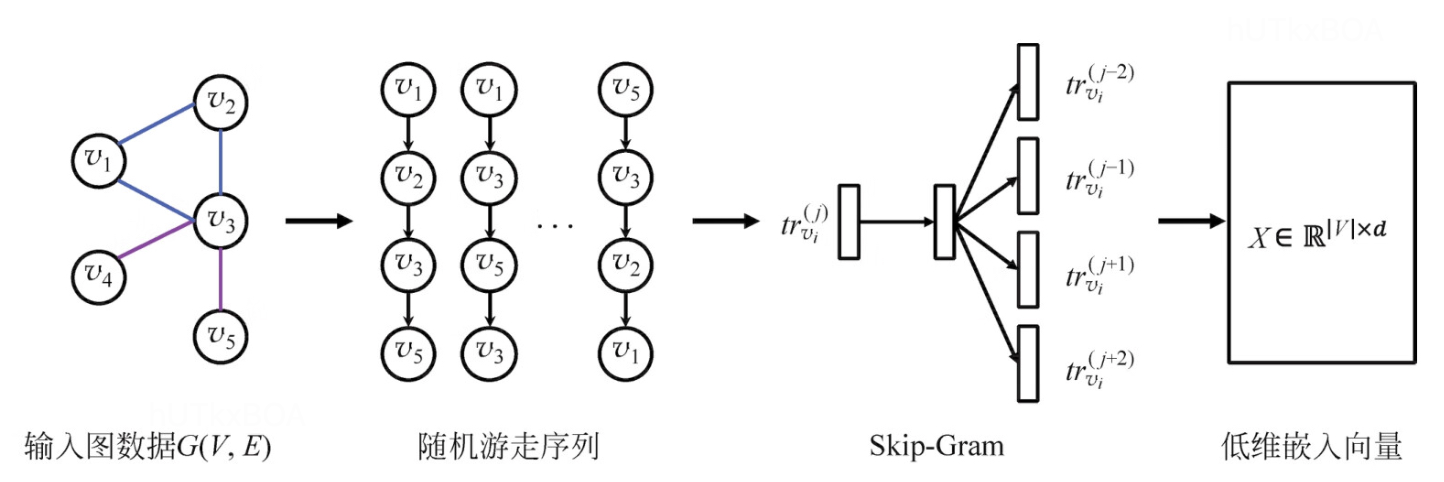
图表示学习其实很大程度上借鉴了word2vec的核心思想,通过构建上下的环境,构建当前词的表达方式。 这里介绍的DeepWalk其实就是一种构建上下文序列的一种方法。顾名思义,就是以当前词为中心,进行深度搜索构建上下文,然后通过序列的映射关系通过神经网络进行图表示学习。DeepWalk生成的图节点表示,更多的还是以两点之间的共现关系界定两点之间的距离相似度。
DeepWalk随机游走流程
随机游走是一种可重复访问的深度优先遍历算法。对于给定一个图中的起始节点,随机游走算法会从其邻居节点中随机抽取一个节点作为下一个节点作为新的其实节点,重复这个过程直到序列长度等于k,就完成了一个序列的表示。可以通过如下的形式化表达。其实节点trvi0,生成随机游走序列trvi0,...,trvk0,这里一般采用平均概率采样。
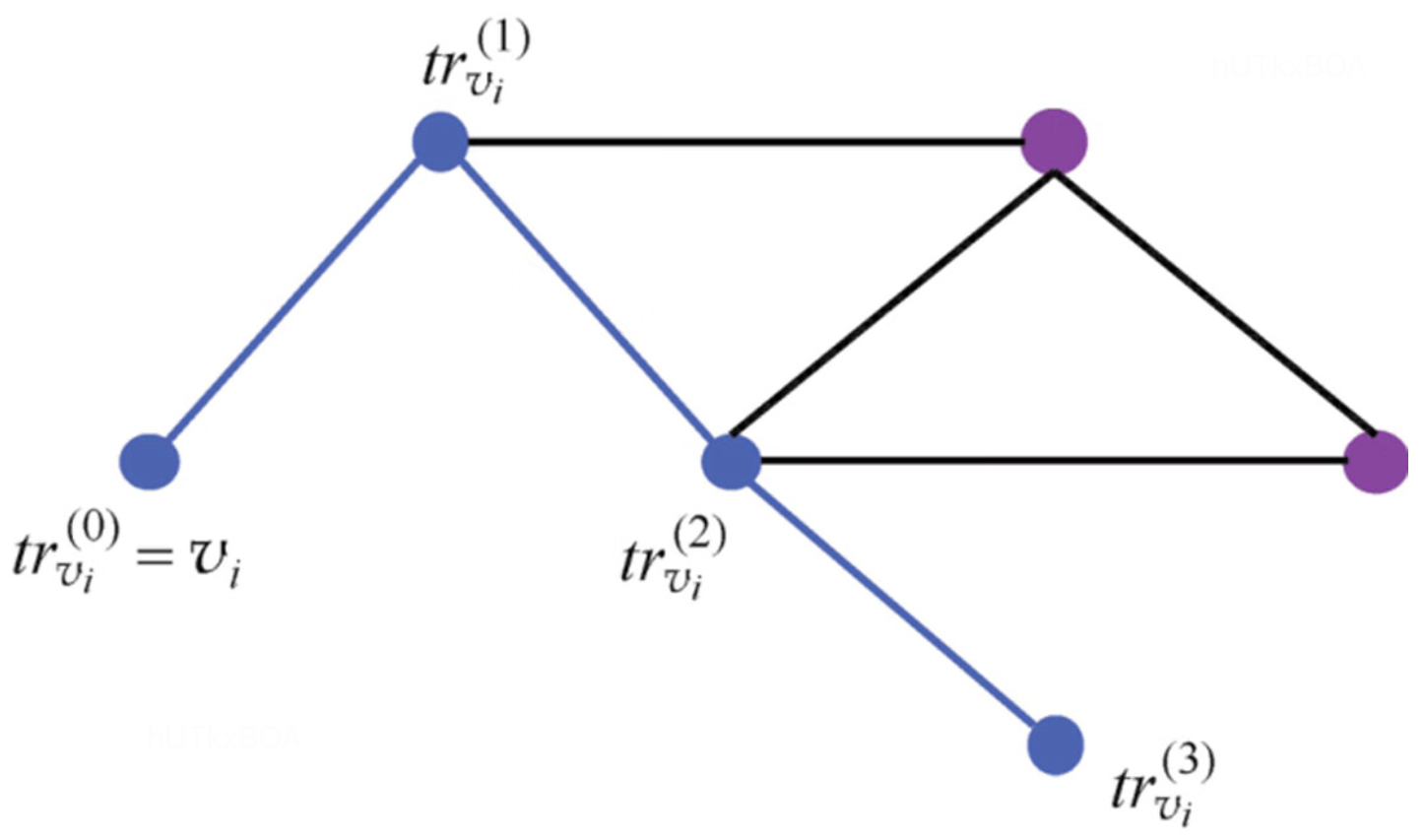
通过这种方式我们能获取一系列的序列表示。引入word2vec后能够完成如下的学习过程。
温馨总结
其实与deepwalk相对应的还有widewalk的方式构建学习序列,但是这两种遍历方式对于业务场景的使用。 对于广度的搜索更多的是关注内容的相似性, 对于深度的搜索关注的是结构的相似性。
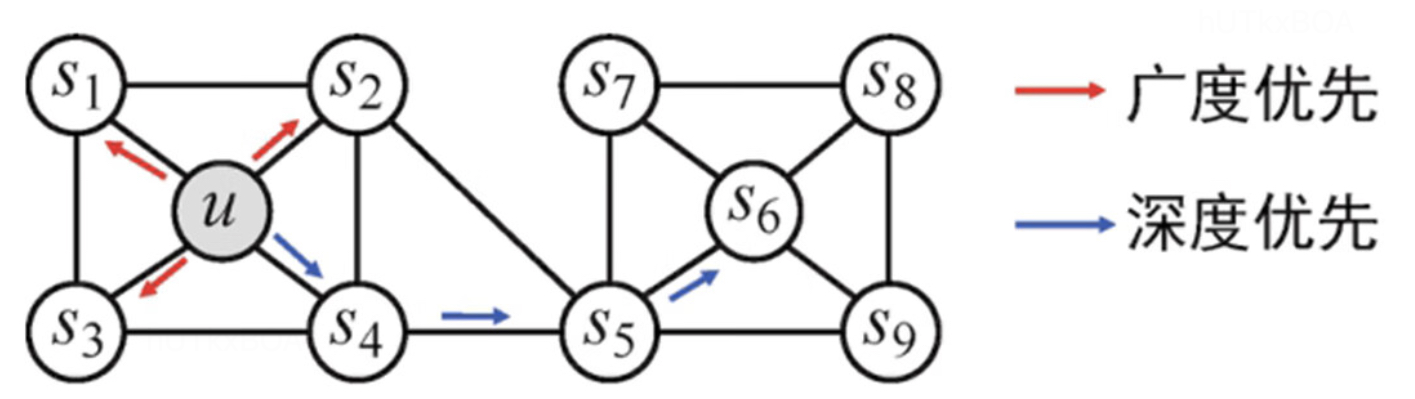
Node2Vec
Node2Vec引入了两步随机游走的算法,第一步从节点t游走到节点v,第二步从节点v游走到其他邻居节点。当然每次跳转的概率并不是确定的,有两个超参数p和q决定的。
\begin{equation}
\alpha(v_{t+1}|v_{t},v_{t-1})=\left\{
\begin{aligned}
\frac{1}{p}\ \ d(v_{t-1}, v_{t+1})=0 \\
1 \ d(v_{t-1}, v_{t+1})=1 \\
\frac{1}{q}\ \ d(v_{t-1}, v_{t+1})=0 \\
\end{aligned}
\right.
\end{equation}
其中d(vt−1,vt+1)表示从节点vt+1到vt−1的最短距离。q>1,游走会倾向于访问和t相连的节点,从而体现BFS特性,q<1,那么随机游走会倾向于访问远离t的节点,就是DFS的属性。如果p>max(1,q),则返回的概率会变得相对较小,这个时候会倾向于不往回走,倾向于DFS特性,如果p<max(1,q),则会返回概率变得较大,这个时候游走会倾向于往回走,多步游走更倾向于围绕起点附近,倾向DFS属性。
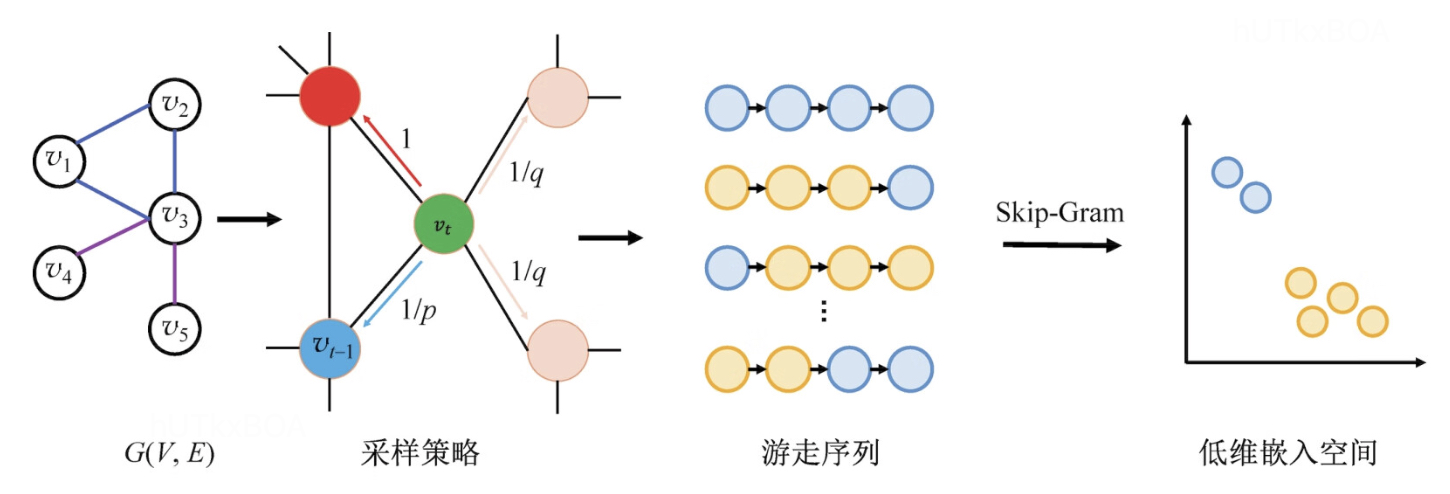
负采样
如果你傻傻的按照Node2Vec算法来做的话,你会发现这个算法的复杂度很高。所以接下来我们说策略实际上是怎么让这个算法在大规模的上落地,首先比较好理解的是负采样降低复杂的的算法,无论是CBOW模式还是skip-gram模型,整个词库词语数量为V,CBOW预测中间词,输出中只有中间词为1,其余词都为0;skip-gram预测周围词,只有周围有限的n个词为1,其余都为0,这两种模式下都是正例数很少,而负例数很多的情形。这种情况下即使你刚刚做模型你也应该知道怎么办? 最本能的反应是正例全用,负例采集一部分,这就是所谓的负采样。
分层softmax
其实这个方法和softmax也没啥关系,只是改造了skip-gram算法。
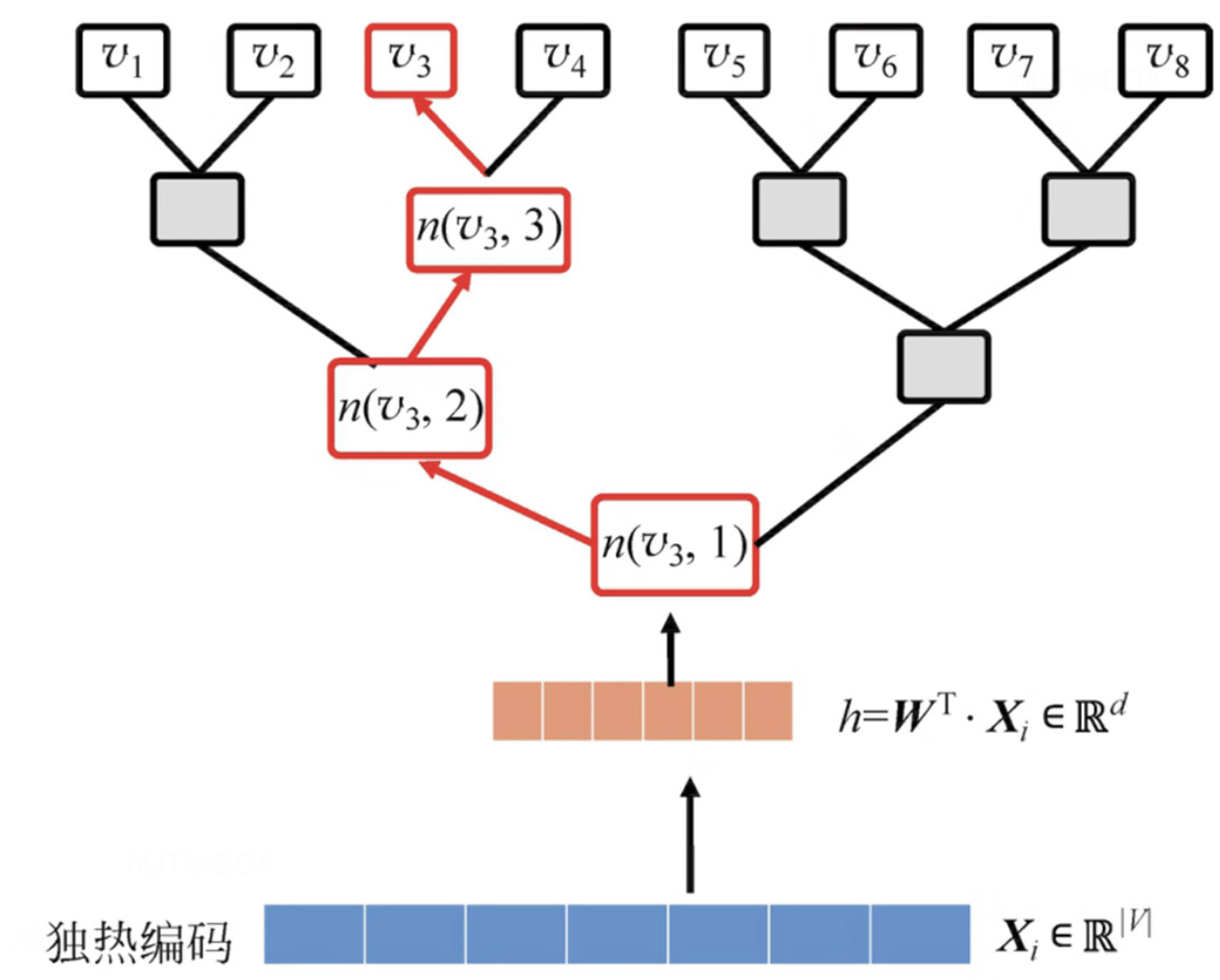
以图G(V,E)为例,以节点的度为权重构建一个霍夫曼树,用霍夫曼树结果来代替skip-gram网络。上图也能看出来,从输入到预测不是一下子出来的,而是沿着霍夫曼树最终到底到节点的。
从上图能看出来,先是独热编码为输入,然后经过一个简单的隐藏层,然后传到到霍夫曼树中,最终到叶子节点完成分类。我们利用这个路径确定预测值是否为该叶子节点的概率P(vp∣vi), 如上图的红色线标注的路径。
P(v3∣v1)=P(n(v3,1),left)×P(n(v3,2),right)×P(n(v3,3),left)(2.1)
n(v3,1)表示到v3节点的第1个霍夫曼节点。P(n(v3,1),left)表示节点n(v3,1)指向做孩子的概率。这里的左右其实是一个二分类问题,可以使用如下的形式表示
P(n(v3,1),left)=δ(θjv3∗hT)P(n(v3,1),right)=1−P(n(v3,1),left)(2.2)
更一般的表达
P(n(vp∣vi)=j=1∑L(vp−1)δ[n(vp,j+1)=ch(n(vp,j))]×θjvp×hT(2.3)
其中ch(n(vp,j))表示n(vp,j)的做孩子,$L(v_{p}-1) $是路径长度。[x]表示当x为true的时候是1,否则为-1. 进一步给出损失函数
L=−lnP(n(vp∣vi)(2.4)
也就是最大化路径的联合概率。这样也把原来O(|V|)的复杂度降低成O(ln|V|)。
其他随机游走算法
LINE
LINE和之前讲的算法最大的不同是LINE既考虑了局部相似度也考率了全局相似度。所以亦能使用与有向图和无向图。如下图所示,一阶关系就是单纯的相邻关系,而二阶关系的定义是指两个节点的邻居具有高度的重叠度。这个在生活中也是经常见到的,例如两个人的共同朋友越多,那么这两个的关系也可能越近。

一阶相似度优化
一阶相似度的目标是尽可能的让两个具有无向变的节点的距离更近,其节点转移的概率分布。
P1(vi,vj)=1+exp(−uiT⋅uj)1(1.1)
ui,uj分别为节点i 和节点j 的embedding向量表示.
其归一化为
P1(vi,vj)=WwijW=i,j∈E∑wij
进而给出一阶优化的目标函数
L1=−i,j∈E∑wijlog(P1(vi,vj))(1.2)
二阶相似度优化
二阶的转移概率定义如下
P2(vj∣vi)=∑kVexp(ujT⋅ui)exp(uj′T⋅ui)(2.1)
其中ui为节点i 的embedding向量,uj′表示节点j的上下文,V表示节点数。进而给出二阶相似度的经验分布定义
P2(vj∣vi)=diwijdi=k∈N(i)∑wik
其中di表示i节点的出度,N(i)表示i的邻近节点。二阶相似度优化的目标是保证转移概率和经验分布尽可能相近,所以目标函数为
L2=i,j∈E∑wijlog(P2(vi∣vi))(2.2)
最后算法训练优化一阶相似度和二阶相似度的模型,然后将两个模型的表示合起来。
异质图的表示
异质图的概念是说当图中的节点不是相同含义的情况下,就产生了异质图,现实生活中典型的就是新闻、话题、热点这样构成的图就是一个异质图, 异质图和不同的图表示其实思想上是一致的, 不过需要一个输入, 我们称为元路径, 这个元路径是说你要制定一个游走关系,例如新闻的下一个游走节点的属性一定是一个话题,类似的就会有一系列的元路径。
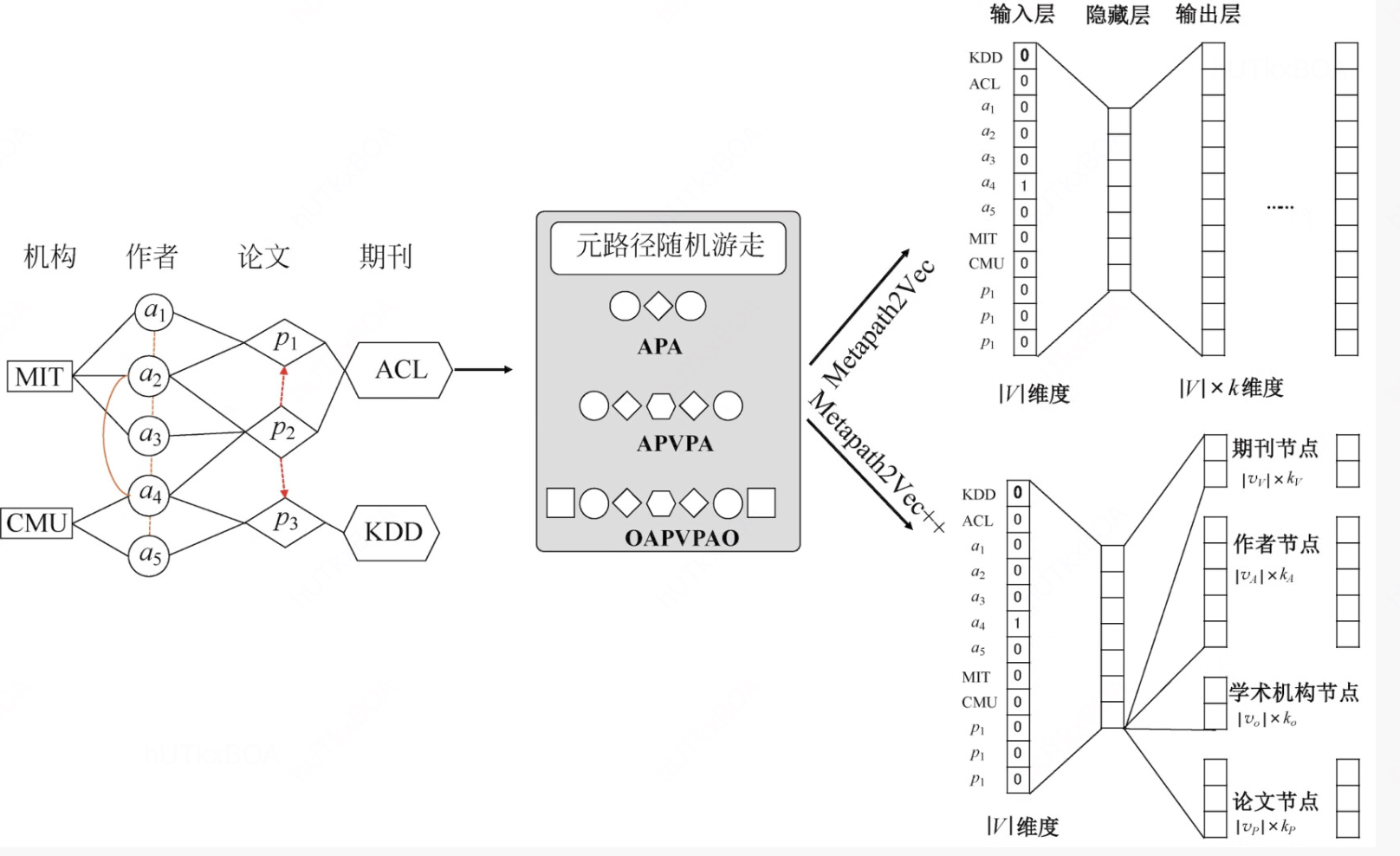
这样咱们也简单的回答了针对异质图的表示问题。