本文想介绍一下MSE这个优化函数,通过MSE这个损失函数来看机器学习中一些底层的理论。
标准方程
J(θ)=E[(y−y^)2](1.1)
公式1.1是均方误差的一个简单的表示,很明显我们就是要求的一个参数能够使得J(θ)最小。最小化的代价函数J(θ)等价于其对θ的梯度为0,则有如下的推导过程
▽J(θ)=▽E[(y−θTx)(y−xTθ)]=▽[E[y2]−2θTE[xy]+θTE[xxT]θ]=−2p+ϕθ=0(1.2)
也可以表达为
ϕθ∗=p(1.3)
其中θ∗表示最优的参数值。同时也称上面的公式为正规方程。
其中,p是输入和输出的互相关向量。
p=[E[x1y],E[x2y],...,E[xly]]=E[xy](1.4)
相应的协方差矩阵为
ϕ=E[xxT](1.5)
如果协方差矩阵是可逆的,就能求解最优线性估计,且解是唯一的,如果是不可逆就有无穷多个解。
特征工程的启发
通过公式1.2对MSE的展开形式, 思考一个有趣的问题, 如果我们想要做一个特征,这个特征符合什么样的特点能够对MSE的收敛更有帮助呢?
这里我们先枚举假设,看看MSE的变化,如果我们加入一个特征X,与Y的相关性较强,与原有的X的相关性也比较强,那么E[XY]增大,但是E[XX]也增大,那么就会导致MSE的变化不可预知是否能变小。当然这就是特征冗余的问题,通过正则项思能解决一部分问题的。
那么假设我们加入一个X’,使得E[XY]增大,但是E[XX]降低,就能十分容易的让MSE减小, 这样的特征的物理概念就是新加入的特征与Y的相关性强,但是与原有的X相关性弱,提供更大的信息增益,所以如果你想找到一个“完美特征”, 你能清楚他的画像吗?
代价函数曲面
根据上文中定义的代价函数可以使用如下的方式表达
J(θ)=σy2−2θTp+θTϕθ(2.1)
将公式2.1加减θ∗Tϕθ∗
J(θ)=J(θ∗)+(θ−θ∗)ϕ(θ−θ∗)(2.2)
其中J(θ∗)如下
J(θ∗)=σy2−2θ∗Tp+θ∗Tϕθ∗=σy2−2θ∗ϕθ∗+θ∗Tϕθ∗=σy2−θ∗Tϕθ∗=σy2−pTθ∗
从上面的公式的能得出一些结论.
- 最优值θ∗的代价总是小于输出变量的方差E[y2]. 如果p=0, 表示x和y不相关。这种情况下,至少就MSE判定标准而言,不能通过观察x对y进行预测。此时的误差与J(θ∗)一致都等于σy2,而则表示的是y在均值为0附近的内在不确定性。相反的如果输入和输出有相关关系,可以消除部分y的不确定性。
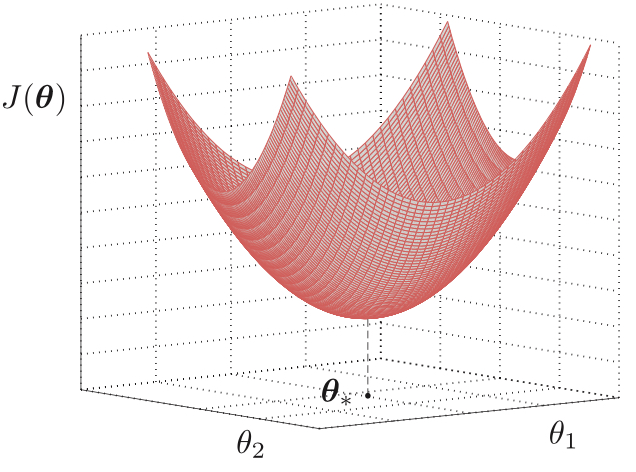
- 除了最优θ∗外的任何θ值,由于ϕ的正定性,如公式2.2中,可知,误差的方差是增加的。且代价函数的MSE曲面如下图。是一个椭圆形,形状取决于ϕ的特征值。
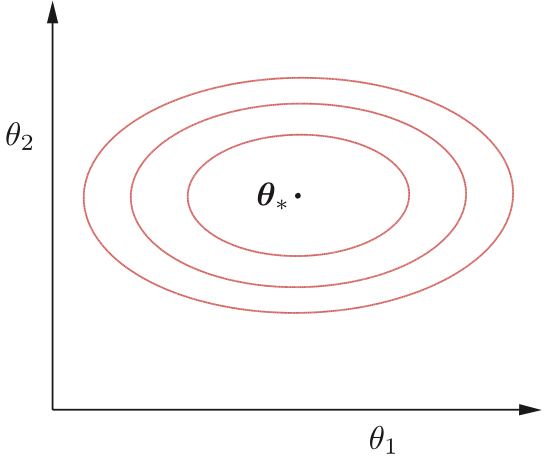
- 如图MSE等高线, 这个等高线的长轴是有输入变量的协方差矩阵ϕ的最大特征值λmax决定,短轴是λmin决定。这里有个小知识点。“最大特征值对应的特征向量方向上包含最多的信息量,如果某几个特征值很小,说明这几个方向信息量很小,可以用来降维,也就是删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用信息量变化不大”。
下图分别展示了MSE曲面和MSE等高线图。
几何理解
首先我们来了解正交的概念,给定两个不相关的随机变量x和y,如果是其内积为0或者是E[x,y]=0就可以称为正交。那么看3.1
y^=θ1x1+...,+θlxl(3.1)
随机变量y^可以解释为向量空间的一个点。它是这个空间中l个元素的组合,因此变量y^必然是这些点张成的自空间中。但是对于真值y却不取决于x的变量,因此我们的目标是想得到一个y^和y的近似,使得e=y−y^的误差最小。可以理解的是当y^,y正交的情况下,这个e最小(欧几里得空间内,直线最短),如下图。也就是
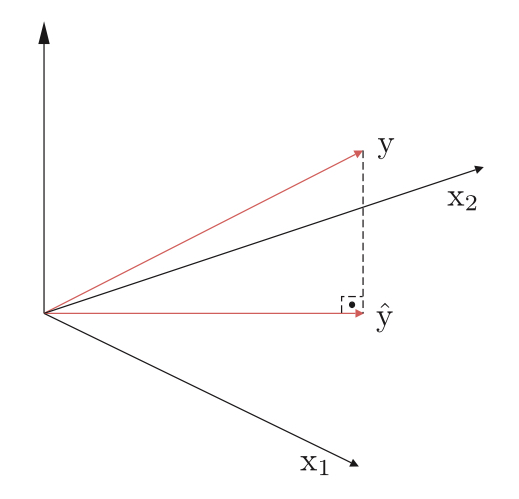
E[ekk]=0k=1,2,3..,l
上面的公式又可以写成
E[(y−i=1∑lθi)xk]=0或者i=1∑lE[xkxi]θi=E[xky]
上面这个公式也是正规方程的一种表达形式,也就是说MSE想要表达是当前输入变量x与y的相关关系,能够通过x的子协方差矩阵和参数θ表达,就能预测出最好的误差效果。
线性回归的例子
y=θox+ηθo∈Rk
其中η是一个与x独立的零均值噪声变量,如果真实系统中θo的维度k能够等于l,也就是把相关的变量全部刻画全,k=l,那么就可能拟合到最优值
θo=θ∗
且最优MSE等于噪声的方差。
滤波
滤波经常也会在机器学习的任务中被提及,也是通过MSE的方式作为评价标准,下面介绍下滤波的三种问题。
- 滤波,在时刻n的估计是基于所有的先前的接受数据信息。
- 平滑,收到到时间区间[0,N]内的数据得到每个时刻n<N的估计
- 预测,基于知道包括时刻n的数据,得到n+x的时间估计