BN(Batch Normalization)
BN是深度学习中缓解过拟合的一个非常常见的手段,不仅能有效的解决梯度爆炸的问题,而且加入了BN的网络往往是更加稳定的还具有一定的正则化的作用。
梯度饱和问题
日常工作中我们经常使用的sigmod激活函数或者tanh激活函数存在饱和的区域,其原因是激活函数输入值过大或者过小,导致的激活函数的梯度接近于0,使得网络收敛过慢。传统的方法是使用Relu激活函数。BN同样也能解决这个问题,它的策略是调用激活函数之前将Wx+b的值归一化到梯度值比较大的区域,假设激活函数为g,BN的激活函数之前使用就如下。
z=g(BN(Wx+b))(1.1)
BN的训练过程
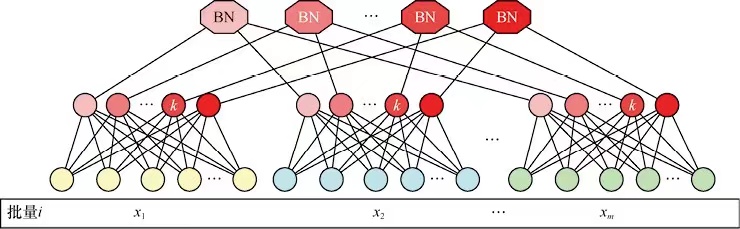
BN的训练过程是以批次为单位的,假设一个批次有m个样本,有d维,那么这个批次每个样本的k个特征归一化如下
xk^=Var(xk)xk−E(xk)(1.2)
其中E和VAR表示第k个特征的这个批次的所有样本的均值和方差。
BN的测试过程
训练的时候,采用SGD的方式可以获得该批次样本的均值和方差,但是使用的时候是单个样本,那么如何使用训练好的模型?在计算BN的输出的时候,我们需要获取均值和方差是通过统计样本得到的。训练的过程中会从训练集合中随机取多个批次的数据集,每个批次m个样本,测试的时候使用的均值和方差就是这些批次的均值和方差。
当然这个过程需要训练完成后再进行数据采样,更多的开源框架训练的时候,顺便把采样的样本的均值和方差保留下来。Keras中,这个变量叫做滑动均值,方差叫做滑动方差,测试的时候就使用这些已经知道的值,进而在测试的时候使用。
CNN中的BN
BN除了可以在MLP中使用,在CNN中表现也比较好,但是在RNN中表现不好。其原因主要在于BN在CNN中的使用方法。CNN和MLP的不同点是CNN中每个样本的隐藏层的输出都是三维的,而MLP是一维的。当在CNN中使用BN的时候,归一化的计量的计算是以通道为单位的。
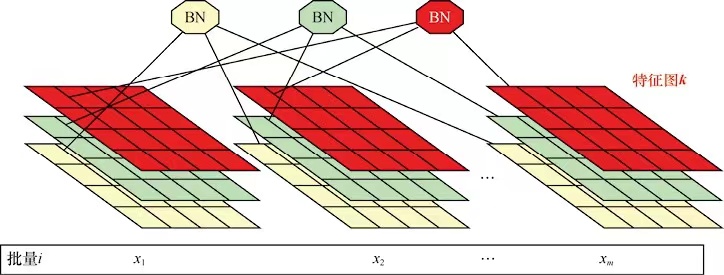
假设一个批次有m个样本,特征尺寸是p×q,通道数维度d,在CNN中,BN的操作以特征图为单位,因此一个BN要统计的数据的个数是m×p×q。
BN的奏效原因
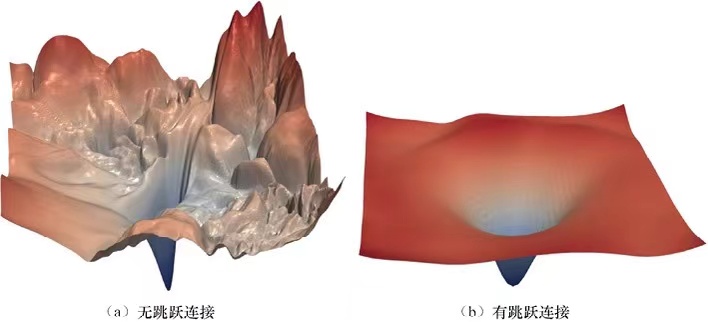
BN的作用是平滑了损失平面,并且残差网络也是起到了平滑了损失平面的作用。。
BN的处理以后的损失函数会满足Lipschitz连续,就是说损失函数的梯度小于一个常数,因此损失平面不会震荡过于剧烈。
LN(layer Normalization)
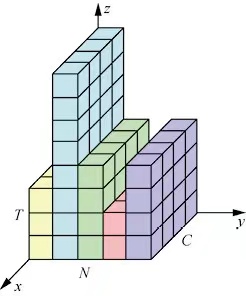
BN不适合RNN等动态网络和批次的尺寸较小的场景。LN能够有效的解决这个问题。LN和BN的不同点是其归一化的维度是相互垂直的.如下图,N表示样本轴,C表示通道数,F表示每个通道的特征数。(b)是BN的方法,它取不同样本的同一个通道进行归一化。而(a)取同一个样本的不同通道进行归一化。
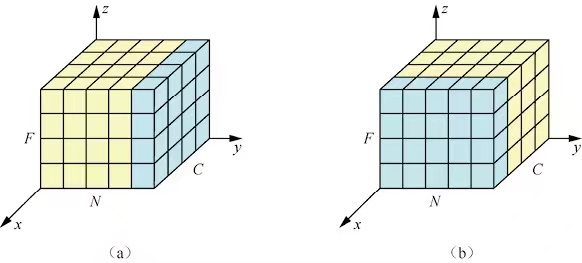
如上图,BN是按照样本数计算归一化的统计量的,但是如果样本很少的情况下,这个统计量不足以反应全局的信息,所以基于少样本的BN效果是十分差的。
BN与RNN
RNN可以展开成一个隐层共享的MLP,随着时间的增多,展开后的MLP的层数也在增多,最终层数由输入数据的时间片决定,所以RNN是一个动态的网络,在一个批次里,通常各个样本长度都是不同的,当统计到比较靠后的时间片时,只有一个样本有数据,基于这样的样本统计不能反应全局分布,所以BN效果不好。
MLP中的LN
这里介绍一些MLp中的LN,设H是一层隐藏节点的数量,I是MLP的层数,我们计算LN的归一化统计量 µ和σ
µl=H1i=1∑Hailσ=H1i=1∑H(ail−µl)2
可以看出上面的统计量和样本数量没有关系,只取决于隐藏节点数量,这样就是使用LN进行归一化统计量。
al^=(σl)2+γal−μl
其中γ是一个很小的常数,只是防止除数为0.在LN中也需要一组参数保证归一化之后不会破坏之前的信息,在LN这个参数叫做增益g和偏置b,假设激活函数为f,那么LN的输出为
hl=f(gl⊙al^+bl)
合并以后
h=f[(σl)2+γg⊙(a−µ)+b]
RNN中的LN
在RNN中可以轻松的使用LN,时刻t的节点其输入时t-1时刻的隐藏层ht−1和t时刻的输入xt.
at=Whhht−1+Wxhxt
接着可以在at上使用归一化操作。
ht=f[(σl)2+γg⊙(at−µt)+b]µt=H1i=1∑Haitσt=H1i=1∑H(ait−µt)2
CNN中的LN
当然如果你尝试将LN添加到CNN中会发现,LN破坏了卷积学习到的特征,模型无法收敛,所以CNN之后使用BN是一个更好的选择。
小结
通过上面的讲解相信大家应该理解了BN和LN的主要区别,BN的效果一般是优于LN的,原因是不同样本、同一特征得到的归一化特征更不容易损失信息。
WN(weight normalization)
WN的做法是将权重向量w在其欧式范数和其方向上解耦成参数向量v 和参数标量g,然后使用SGD分别优化两个参数。
WN也是和样本数量无关的,可以使用RNN等动态网络中。WN一般使用在生成模型、强化学习等噪声敏感的环境中WN效果优于BN。WN也没有额外的参数,计算效率也优于BN。
神经网络的一个节点计算可以表示为
y=ϕ(wx+b)
WN提出的归一化是将w分解成一个参数向量v和一个参数向量g。
w=∣∣v∣∣gv
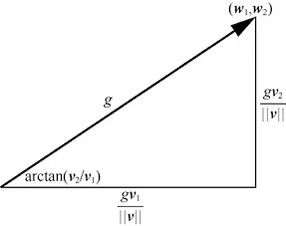
其中||v||表示v的欧式范数,g=|w|,v 表示w的单位方向。当我们固定g=||w||的时候,这个时候相当于仅仅和优化方向v。当v固定的时候就是优化w的范数。
WN原理
v和g更新值的时候可以通过SGD计算如下
▽gL=∣∣v∣∣▽wLv▽vL=∣∣v∣∣g▽wL−∣∣v∣∣2g▽gLv
其中L是损失函数,▽wL为我在L下的梯度值,就可以看出这个过程中没有引入新的参数值。
可以推导上面的公式
▽vL=∣∣v∣∣g▽wL−∣∣v∣∣2g▽gLv=∣∣v∣∣g▽wL−∣∣v∣∣2g∣∣v∣∣▽wLvv=∣∣v∣∣g(I−∣∣v∣∣2vv′)▽wL=∣∣v∣∣g(I−∣∣w∣∣2ww′)▽wL=∣∣v∣∣gMw▽wL
其中Mw=I−∣∣w∣∣2ww′. 导数第二步的推导是因为v和w是同方向的,通过上面的推导反应了WN的两个重要特性。
- ∣∣v∣∣g表明WN会对权重梯度进行∣∣v∣∣g的缩放
- Mw▽wL表明WN会将梯度映射到一个远离▽wL的方向,因为相当与1-xx。
这两个特性会加速模型的收敛
WN的参数初始化
由于WN不像BN有规范化特征尺度的作用,因此WN的初始化需要谨慎。
- v使用均值为0,标准差为0.05的正态分布初始化
- g和偏置b使用第一批训练样本的统计量进行初始化
g←σ[t]1b←σ[t]−μ[t]
使用样本进行初始化,因此这种初始化方法不适用与RNN类的模型。
IN(Instance Normalization)
对于像图像风格迁移这类任务,每个样本的每个像素点信息都很重要,对于BN这种每个批次的所有样本进行归一化的方法是不太适合的,同理LN需要考虑一个样本所有通道的算法可能忽略不同通道之间的差异,也不太适应。
IN是为这种场景诞生的,一种更加适合单个像素有更好要求的场景,如风格迁移,GAN等。IN的算法十分简单,计算归一化的统计量的时候考虑单个样本,单个通道的所有元素。这里就不再深入介绍啦。
GN(group Normalization)
GN是介于LN和IN之间的一种方案,通过将通道数分成几组归一化统计量,GN也是和批次大小无关的算法,所以可以用在批次小的算法中。
µi=m1k∈Si∑xkσi=m1k∈Si∑(xk−µi)2−βxi^=σi1(xi−µi)
这里的区别就是Si是如何取得的,对于BN来讲是从不同批次的同一个通道中获取所有的值,对于LN来讲是用通过同一个批次的不同通道上取所有的值。对于IN来讲是既不跨批次,也不跨通道,GN是将通道分成若干组,在组内进行统计。G实际上是一个超参数。 GN能够奏效的核心原因是如果一个特征图卷积足够多,必然有一些通道的特征是类似的,因此可以将这些类似的特征进行归一化处理。
SN(switchable Normalization)
SN的算法核心是提出一个可微的归一化层,可以容模型根据数据学习归一化方法。
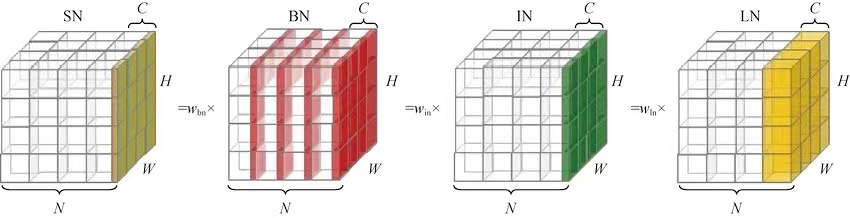
所以SN与任务无关,所有的任务都可以使用SN进行归一化。
强力补充
这里顺便再介绍一个东西,解决梯度爆炸这样的问题还可以使用梯度裁剪的方式。梯度裁剪(gradient clipping)是一种常用的优化技巧,旨在防止梯度爆炸(gradient explosion)问题。在深度学习中,特别是在循环神经网络(RNN)中,由于反向传播计算梯度时存在链式法则,长序列会使得梯度值变得非常大,导致权重参数更新过于剧烈,从而影响模型的训练效果。梯度裁剪就是限制梯度值的大小,以防止梯度爆炸问题的发生。
梯度裁剪的实现方式很简单,可以在反向传播求梯度后,计算出梯度的范数(即 L2 范数),然后将其与一个阈值进行比较,如果超过了阈值,则将梯度按比例缩放到阈值以下,否则不做处理。这样就防止梯度增加过快带来的梯度爆炸的问题。