机器学习之Dropout

本文主要介绍两类常以网络层形式添加模型结构中，一类是Dropout，一类是归一化。

Dropout

Dropout是当发生过拟合以后，第一个考虑使用的网络结果。在训练时，通过将一些节点替换成掩码来减轻节点之间的耦合性，从而起到正则的效果。
当没有添加Dropout的网络是需要全部节点进行学习，而添加了Dropout的网络只需要对其中没有替换为掩码的节点进行训练。
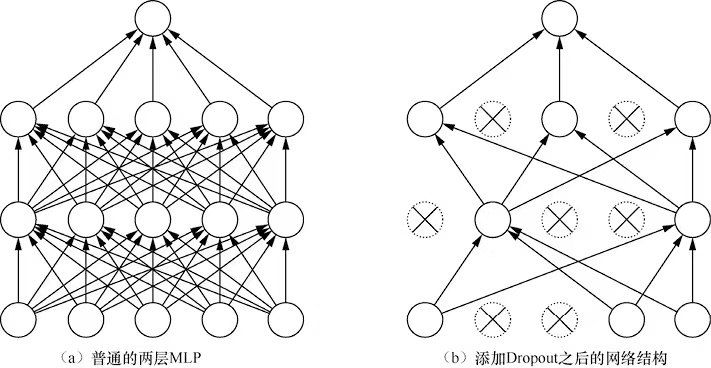
Dropout区别
以上就是添加了Dropout的网络的机构。其实在没有Dropout之前，一般是使用L1和L2正则项的方式解决过拟合的问题。但是没有完全的解决这个问题，以为网络存在共适性的问题。所谓的共适性是指网络中的一些节点有更强的表征能力，随着网络不断训练，具有更强表征能力的节点被不断强化，而表征能力比较弱的节点会别不断弱化，知道可以忽略不计。这个时候的网络只有部分节点是被训练的，浪费了网络的宽度和深度，导致效果提升受到限制。而Dropout能够很好的解决这个问题。

Dropout数学原理

咱们通过一个简单的单层神经网络举例，它的输出是输入的加权和。

O=\sum w_{i} I_{i} \tag{1.1}

单层网络
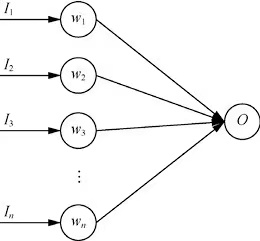
上图是一个无Dropout网络的结构，它的误差 $E_{n}$ 可以如下表示，t是目标值

E_{n}=\frac{1}{2}(t-\sum w'_{i} I_{i})^{2} \tag{1.2}

这里是使用的是w’,是为了找到无Dropout的网络和之后的添加了Dropout的网络的区别， $w'=pw$ ,p是概率值。那么公式1.2就有如下的表示

E_{n}=\frac{1}{2}(t-\sum pw_{i} I_{i})^{2} \tag{1.3}

对于公式1.3求导数

\frac{\partial E_{n}}{\partial w_{i}}=-t_{i}p_{i}I_{i}+w_{i}p_{i}^{2}I_{i}^{2}+\sum_{j=1}^{n} w_{j}p_{i}p_{j}I_{i}I_{j} \tag{1.4}

当我们对公式1.3进行Dropout以后，他的误差就变成如下表达

E_{D}=\frac{1}{2}(t-\sum \sigma_{i} w_{i} I_{i})^{2} \tag{1.5}

其中 $\sigma$ 服从伯努利分布，有p的概率为1，有1-p的概率为0，同样对1.5求导

\frac{\partial E_{D}}{\partial w_{i}}=-t_{i}\sigma_{i}I_{i}+w_{i}\sigma_{i}^{2}I_{i}^{2}+\sum_{j=1}^{n} w_{j}\sigma_{i}\sigma_{j}I_{i}I_{j} \tag{1.6}

对公式1.6求期望

E(\frac{\partial E_{D}}{\partial w_{i}})=-t_{i}p_{i}I_{i}+w_{i}p_{i}^{2}I_{i}^{2}+w_{i}Var(\sigma_{i})I_{i}^{2}+\sum_{j=1}^{n} w_{j}p_{i}p_{j}I_{i}I_{j} \\ =\frac{\partial E_{n}}{\partial w_{i}}+w_{i}Var(\sigma_{i})I_{i}^{2} \\ =\frac{\partial E_{n}}{\partial w_{i}}+w_{i}p_{i}(1-p_{i})I_{i}^{2} \tag{1.7}

通过1.6和1.7能够看出，带有Dropout的网络的梯度的期望等价于带有正则的普通网络，正则项为 $w_{i}p_{i}(1-p_{i})I_{i}^{2}$

Dropout的小技巧

通过上面的证明我们知道了，当丢失率为0.5的时候，Dropout网络具有最强的正则效果。因为(1-p)p在p=0.5的时候取得最大值。
丢失率的选择上，当网络比较浅层的时候，会选择丢失率比较小的数字，一般是0.2，当我网络比较大的时候，一般选择0.5.

CNN中的Dropout

CNN的特征图是有由长宽高组成的三维矩阵。按照传统的Dropout，它丢弃的应该是特征上的像素。但是这个方法不是很奏效，其原因是临近像素之间具有相似性。他们不仅具有相近的邻居。相似的感受野和相同的卷积核，所以即使丢弃也能够通过相邻居节点找回来，随意针对CNN单独设计了Dropout。
一般有三种方式。
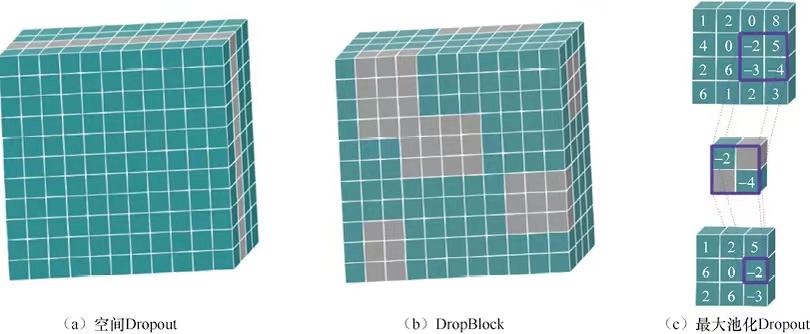
CNN中的Dropout
一种方式是直接通过丢弃通道的方式实现Dropout，这样缓解通道之间的共适问题。也可以随机的丢失一大片区域的像素，这种方法叫做DropoutBlock。最后一种方法是执行最大池化之前，将窗口的像素随机替换成掩码，这样使得窗口内的较小的值也有机会影响网络的效果。