今天我们来介绍运筹优化中的一类问题，存储论问题。在日常生活中通常需要最合理、最经济的存储问题。例如水库蓄水问题等，接下来就来介绍一个存储论包括的相关概念。

1. 需求
2. 补充
3. 费用（存储费，订货费，生产费，缺货费）
4. 存储策略

其中存储策略包括几种方式。

• t-循环策略， 每个固定的时间t，补充一个固定的存储量Q
• （t，S）存储策略，每隔一个固定的时间补充一次，补充的数量不固定，看实际存储量确定，如果实际存储量为L，那么补充数量就是Q=S-L。S是最大存储量
• （s,S）策略，每经过t时间检查存储量L，当L>S的时候不进行补货，否则补充Q=S-L，s称为订购点。
• （t,s,S）策略，每经过时间t检查存储量L，当L>S不进行补货，当l<S补充存储L，让其达到S。

模型一，备货时间很短，不允许缺货

模型假设

1. 当存储降低为0的时候，可以瞬间补充，备货时间为0
2. 需求是连续均匀的，设需求的速度C为常数$R_{2}$
3. 每次订货量不变，订货费不变，订货费$C_{3}$
4. 单位时间内单位存储费不变，存储费为$C_{1}$
5. 不允许缺货，单位缺货费$C_{2}$且无穷大
6. 采用t-循环策略，间隔为t，每次补充量Q

构建模型

t时间内的平均存储量为

$$\frac{1}{t} \int_{0}^{t}R_{2}TdT=\frac{1}{2}R_{2}t \tag{1.1}$$

平均的存储费为$\frac{1}{2}C_{1}R_{2}t$
假设货物的单价是P，订购费为$C_{3}+PQ=C_{3}+PR_{2}t$,从而t时间内平均订购费为$\frac{C_{3}}{t}+PR_{2}$,。平均总费用为

$$C(t)=\frac{1}{2}C_{1}R_{2}t+\frac{C_{3}}{t}+PR_{2} \tag{1.2}$$

求最佳的时间t，需求要求导

$$\frac{dC(t)}{dt}=0\\ \frac{1}{2}C_{1}R_{2}-\frac{C_{3}}{t^{2}}=0 \tag{1.3}$$

最后求的$t=\sqrt{\frac{2C_{3}}{C_{1}R_{2}}}$,最佳的补货量为$Q=R_{2}t=\sqrt{\frac{2C_{3}R_{2}}{C_{1}}}$。此时最小的平均总费用为

$$C=C(t)=\sqrt{2C_{1}C_{3}R_{2}}+PR_{2}\tag{1.4}$$

可以发现货物的单价P和最佳的补货量Q无关，为了计算方面，可以不考虑$PR_{2}$，那么C就用如下的表达式

$$C=C(t)=\sqrt{2C_{1}C_{3}R_{2}}\tag{1.5}$$

生产需要一定的时间，不允许缺口

这个模型除了生产需要一定的时间，其余上文的条件相同。设生产批量为Q，所需要的时间为T，生产速度为$R_{1}=\frac{Q}{T}$, 需求速度为$R_{2}， R_{2}<R_{1}$,此时生产的产品满足需求后剩余部分作为存储，如下图所示。

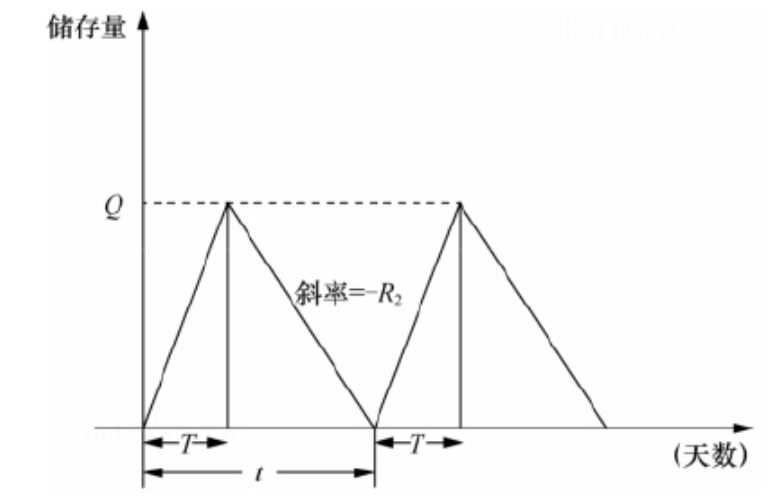
在[0,T]内，存储量以$R_{1}-R_{2}$的速度增加，[T,t]区间内，存储以$R_{2}$速度减少，从上图能看出来

$$(R_{1}-R_{2})T=R_{2}(t-T) \tag{2.1}$$

从而$R_{1}T=R_{2}t$，所以

$$T=\frac{R_{2}t}{R_{1}} \tag{2.2}$$

t时间内平均的存储量为$\frac{1}{2}(R_{1}-R_{2})T$, t时间内的存储费用为$\frac{1}{2} C_{1}(R_{1}-R_{2})T$,设$C_{3}$为t时间内所需要的转配费，那么单位时间的总费用为

$$C(t)=\frac{1}{t}[\frac{1}{2} C_{1}(R_{1}-R_{2})Tt+C_{3}]\\ =\frac{C_{3}}{t}+\frac{1}{2R_{1}} C_{1}(R_{1}-R_{2})R_{2}t \tag{2.3}$$

这个似乎引入导数$\frac{dC(t)}{dt}=0$,求得

$$t=\sqrt{\frac{2C_{3}R_{1}}{C_{1}R_{2}(R_{1}-R_{2})}} \tag{2.4}$$

t就是最佳的周期，最佳的产量为

$$Q=R_{2}t\\ =\sqrt{\frac{2C_{3}R_{1}R_{2}}{C_{1}(R_{1}-R_{2})}} \tag{2.5}$$

最小平均费用为

$$C(t)=\sqrt{2C_{3}C_{1}R_{2}\frac{R_{1}-R_{2}}{R_{1}}} \tag{2.6}$$

最佳生产时间为

$$T=\frac{R_{2}t}{R_{1}}=\sqrt{\frac{2C_{3}R_{2}}{R_{1}C_{1}(R_{1}-R_{2})}} \tag{2.7}$$

可以对比模型一，当R_{1} 趋近与无穷的时候，两个公式是相等的。进入存储的最高数量为

$$S=Q-R_{2}T=\sqrt{\frac{2C_{3}R_{1}R_{2}}{C_{1}(R_{1}-R_{2})}}-R_{2}\sqrt{\frac{2C_{3}R_{2}}{C_{1}R_{1}(R_{1}-R_{2})}} \\ =\sqrt{\frac{2C_{3}R_{2}(R_{1}-R_{2})}{C_{1}R_{1}}} \tag{2.8}$$

模型三，备货时间很短，允许缺货

允许缺货表明企业在存储量降低为0的情况下，还可以等一段时间订货，且缺货的损失很小，允许缺货是对企业有利的。

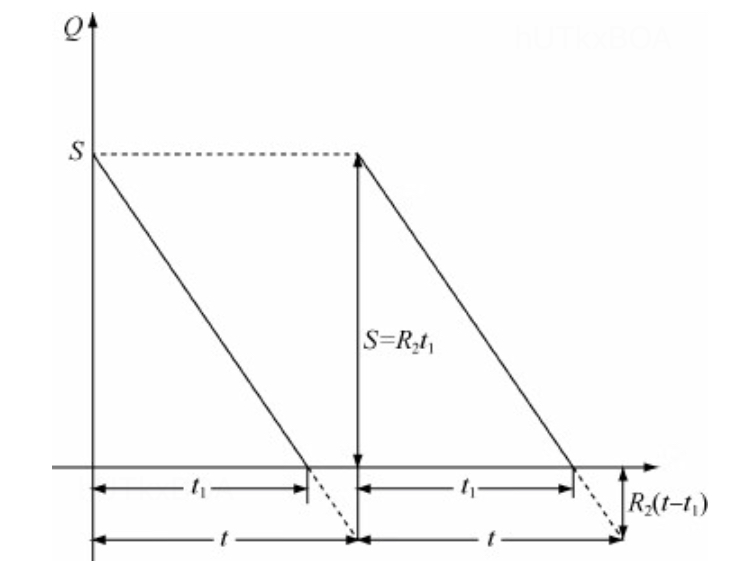
假设最初的存储量为S，可以满足t1的时间需求，那么

$$S=R_{2}t_{1} \tag{3.1}$$

在(t-t1)的时间范围内，平均的缺货量为$\frac{1}{2}R_{2}(t-t_{1})$，则在t时间内的存储费用为

$$C_{1}\frac{1}{2}St_{1}=\frac{1}{2} C_{1} \frac{S^{2}}{R_{2}} \tag{3.2}$$

在t时间内的缺货费为

$$C_{2}\frac{1}{2} R_{2}(t-t_{1})(t-t_{1})=\frac{1}{2} C_{2}\frac{(R_{2}t-S)^{2}}{R_{2}} \tag{3.3}$$

所以备货时间很短和允许缺货的条件下，t时间内的平均总费用为

$$C(t,S)=\frac{1}{t}[C_{1}\frac{S^{2}}{2R_{2}}+C_{2}\frac{(R_{2}t-S)^{2}}{2R_{2}}+C_{3}] \tag{3.4}$$

分别求偏导数$\frac{\partial C}{\partial S}=0, \frac{\partial C}{\partial t}=0$,求得

$$t=\sqrt{\frac{2C_{3}(C_{1}+C_{2})}{C_{1}R_{2}C_{2}}} \tag{3.5}$$

最优的存储为

$$S=\sqrt{\frac{2C_{2}C_{2}R_{2}}{C_{1}(C_{2}+C_{1})}} \tag{3.6}$$

最小费用为

$$C(t,S)=\sqrt{\frac{2C_{1}C_{2}C_{3}R_{2}}{C_{2}+C_{1}}} \tag{3.7}$$

模型四，生产需要时间，允许缺口

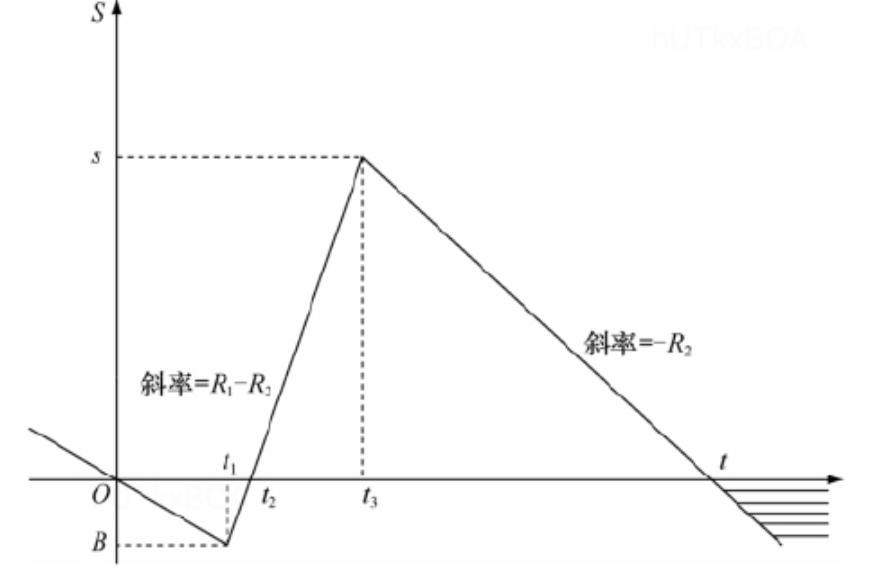
设[0,t]为一个周期，t1为开始生产的时刻，B表示最大的缺货量，[t1,t2]时间内除了满足需求外，补充[0,t1]的缺货。[t2,t3]时间内$R_{1}-R_{2}$的速度增加存储，S表示存货量，在t3时刻停止生产并达到最大值，然后在[t3,t]时间内存储量的需求速度$R_{2}$减少，实际上

$$B=R_{2}t_{1}=(R_{2}-R_{1})(t_{2}-t_{1})\\ t_{1}=\frac{R_{1}-R_{2}}{R_{1}}t_{2} \tag{4.1}$$

最大的存储量为

$$S=(R_{1}-R_{2})(t_{3}-t_{2})=R_{2}(t-t_{3}) \\ t_{3}=\frac{R_{2}}{R_{1}}t+(1-\frac{R_{2}}{R_{1}})t_{2}\tag{4.2}$$

进而求得

$$t_{3}-t_{2}=\frac{R_{2}}{R_{1}}(t-t_{2})\tag{4.3}$$

在[0,t]的时间内费用包括

存储费

$$C_{1}S(t-t_{2})=\frac{1}{2}C_{1}(R_{1}-R_{2})(t_{3}-t_{2})(t-t_{2})\\ =\frac{1}{2}C_{1}(R_{1}-R_{2}) \frac{R_{2}}{R_{1}}(t-t_{2})^{2} \tag{4.4}$$

缺货费

$$C_{2} \frac{1}{2} B t_{2}=C_{2} \frac{1}{2} R_{2} t_{1} t_{2}\\ =\frac{1}{2} C_{2}R_{2} \frac{R_{1}-R_{2}}{R_{1}}t_{2}^{2} \tag{4.5}$$

装配费

$$C(t,t_{2})= \frac{1}{t}[ \frac{1}{2} C_{1}(R_{1}-R_{2})\frac{R_{2}}{R_{1}}(t-t_{2})^{2}+ \frac{1}{2} C_{2}R_{2} \frac{R_{1}-R_{2}}{R_{1}}t_{2}^{2}+C_{3}] \\ =\frac{1}{2} \frac{(R_{1}-R_{2})R_{2}}{R_{1}}[C_{1}t-2C_{1}t_{2}+(C_{1}+C_{2})\frac{t_{2}^{2}}{t}]+\frac{C_{3}}{t} \tag{4.6}$$

分别求导$\frac{\partial C}{\partial t}=0, \frac{\partial C}{\partial t_{2}}=0$。

$$t=\sqrt{\frac{2C_{3}R_{1}(C_{1}+C_{2})}{C_{1}R_{2}C_{2}(R_{1}-R_{2})}} \\ t_{2}=\frac{C_{1}}{C_{1}+C_{2}} t \tag{4.7}$$

订货量Q为

$$Q=R_{2}t=\sqrt{\frac{2C_{3}R_{1}R_{2}(C_{1}+C_{2})}{C_{1}C_{2}(R_{1}-R_{2})}} \tag{4.8}$$

最大存储量为

$$S=R_{2}(t-t_{3})=R_{2}(t-\frac{R_{2}}{R_{1}}t-\frac{R_{1}-R_{2}}{R_{2}}t_{2}) \\ =R_{2}(t-\frac{R_{2}}{R_{1}}t-\frac{R_{1}-R_{2}}{R_{1}}\frac{C_{1}}{C_{2}+C_{1}}t) \\ =\sqrt{\frac{2C_{3}R_{2}C_{2}(R_{1}-R_{2})}{C_{1}R_{1}(C_{1}+C_{2})}} \tag{4.9}$$

最大缺货量为

$$B=R_{2}t_{1}=\frac{R_{2}(R_{1}-R_{2})}{R_{1}}t_{2}\\ =\frac{R_{2}(R_{1}-R_{2})}{R_{1}}\frac{C_{1}}{C_{1}+C_{2}}t \\ =sqrt{\frac{2C_{1}C_{3}R_{2}(R_{1}-R_{2})}{(C_{1}+C_{2})C_{2}R_{1}}} \tag{4.10}$$

最小平均费用为

$$C(t,t_{2})=\sqrt{\frac{2C_{1}C_{2}C_{3}R_{2}(R_{1}-R_{2})}{R_{1}(C_{1}+C_{2})}} \tag{4.11}$$

模型五，价格有折扣的存储问题

一般而言当货物购买量大的情况下，价格是存在折扣的，订货量为Q，对应的货物单价为P(Q), 其中Q是一个集合，其中$Q_{i}$表示价格折扣点， $P_{i}$表示当前的价格。
类似模型一，存储周期的平均费用为

$$C(t)=\frac{1}{2} C_{1}R_{2}t+\frac{C_{3}}{t}+R_{2}P(Q) \tag{5.1}$$

其中$Q=R_{2}t$, C(t)是一个分段的函数，最小费用点为t=\sqrt{\frac{2C_{3}}{C_{1}R_{2}}}}, 但是考虑货物的总价C(t)是也一个逐段下降的趋势，最佳的订货量Q按照下列步骤进行确定。

第一步， $Q=R_{2}t=\sqrt{\frac{2C_{3}R_{2}}{C_{1}}}$, 平均费用为$C=\sqrt{2C_{1}C_{3}R_{2}}+R_{2}P_{j}$, 其中P代表当前段内的价格。
第二步,计算$C^{(i)}=\frac{1}{2} C_{1}R_{2} \frac{Q_{i}}{R_{2}}+\frac{C_{3}R_{2}}{Q_{i}}+R_{2}P_{i}=\frac{1}{2}C_{i}Q_{i}+\frac{R_{2}C_{3}}{Q_{i}}+R_{2}P_{i}$
第三步， 如果$min[C,C^{(j)},...,,C^{(n)}]=C^{*}$, 那么这个C对应的批量就是最小费用订购的批量Q，订阅周期为$t=\frac{Q}{R_{2}}$