神经网络
神经网络是比较初级的一个深度学习模型,但是它的变形有很多种,因为其不可解释的特性,也给这种模型蒙上一层面纱,本章就讲解这个神经网络。
下图就是一个简单的神经网络的结构,从整体上看分为输入层、隐藏层、输出层。
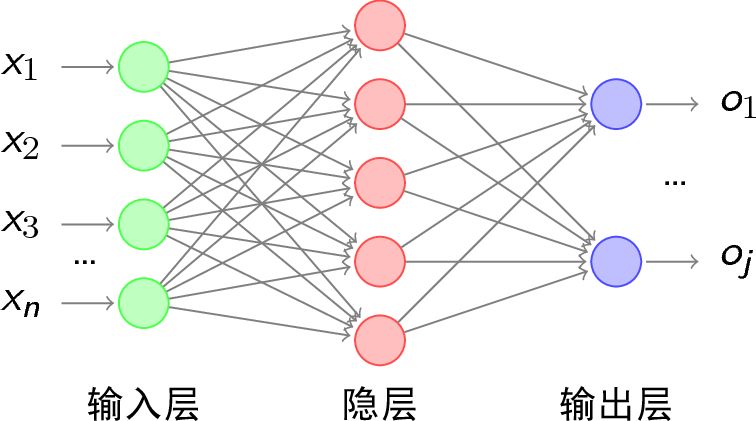
损失函数
首先要确定损失函数是凸函数还是非凸函数,如果是凸函数,那么将会不依赖选取的初始值,一定能找到凸优化的全局最优解,但是如果损失函数为非凸函数,这个就有些特殊了,这个时候参数初始化的值就比较重要,如果选取的不好那么就一定会在局部最优上出不来,相反的如果选取的好也是可能找到全局最优的。
整个网络的方向传播过程也比较简单,利用损失函数求导,更新每一层的参数,直到收敛为止,这里需要注意的是,如果神经网格过于深,会导致损失越传递到输入层,权重更新的越小,也就是梯度消失的意思。
深度前馈神经网络的学习范式
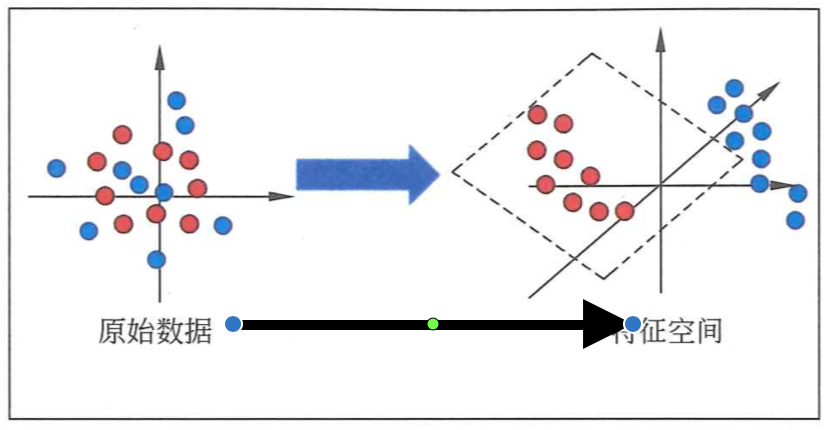
上图十分形象的说明了神经网络的传播到底对数据做了什么,通过对数据进行稀疏转换等操作,找到一个更加高纬度的空间构建样本分类。
那么神经网络的缺点有哪些?
- 训练阶段如果参数较多而样本较少,那么就会出现过拟合的现象
- 优化的目标函数非凸函数,对初始值选取要求较高,否则会出现欠拟合。
- 利用反向传播优化参数可能出现梯度消失的问题。
从物理的角度来讲,前馈神经网络的所有传播无非解决以下几种变换
- 升维或降维
- 放大或缩小
- 旋转
- 平移
- 扭曲或弯曲(非线性完成)
那么我们不断的传播,调整参数细节上到底做了什么呢?
小结
本文没有介绍具体的求导过程,这个是神经网络的原理,数学基础,但是也是相对简单的部分,主要集中在链式求导上比较繁琐,我倒是觉得大家反而不用太关心,但是比较重要的是神经网络到底对我们的数据做了什么?为什么其他模型不能解决,它就能可以。