之前的章节中我们知道,xgboot是可以根据不同场景自定义损失函数的,如果我有一个损失函数,那么我究竟如何通过自定义的方式给到xgb呢,以及我最终的一阶导数和二阶导数到底是相对谁而言的呢?
自定义损失函数
这里我通过一个完整的例子来看看如果我有一个损失函数,怎么使用到我的xgboost模型的。
我们来看一个回归的损失函数Los-Cosh,这个损失函数的原始定义如下。
loss(y,yi)=0∑nlogcosh(yi−y)
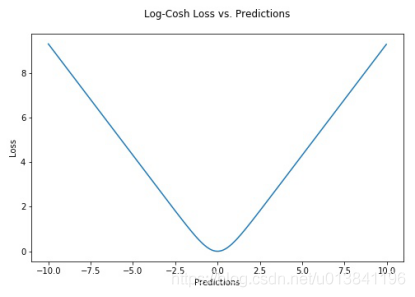
优点
- 对于较小的X值,log(cosh(x))约等于x2/2;对于较大的X值,则约等于abs(x) - log(2)。这意味着Log-cosh很大程度上工作原理和平均方误差很像,但偶尔出现错的离谱的预测时对它影响又不是很大。它具备了Huber损失函数的所有优点,但不像Huber损失,它在所有地方都二次可微。
- Log-cosh也不是完美无缺。如果始终出现非常大的偏离目标的预测值时,它就会遭受梯度问题。
对于这样的一个函数,他怎么放到我们的xgboost中使用呢?
首先我们来看这个函数的求导过程。
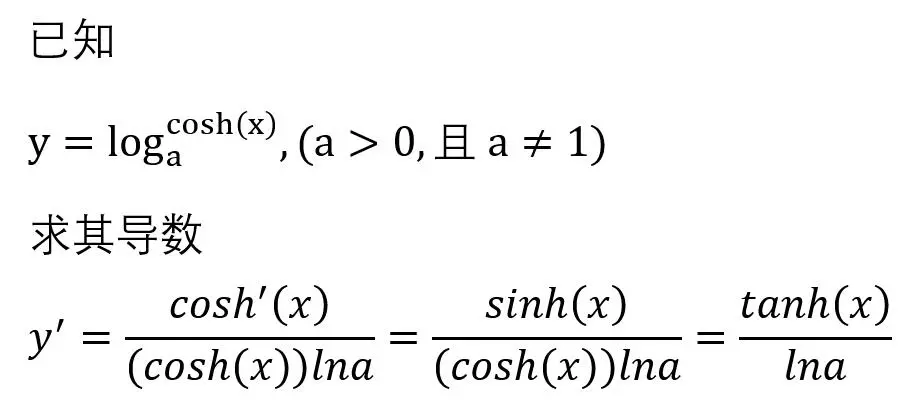
我们发现一阶导数就是tanh(x),二阶导数是cos(x)21,我们在xgboost中做如下的使用
def log_cosh_obj(real, predict):
x = predict - real
grad = np.tanh(x)
# hess = 1 / np.cosh(x)**2 带除法的原方法,可能报ZeroDivisionException
hess = 1.0 - np.tanh(x) ** 2
return grad, hess
这样就能够在我们训练模型的时候修改xgb的损失函数,这里有一个问题需要注意,我们在使用xgb损失函数的时候这个一阶导数二阶导数是相对谁的呢?从上面的计算过程发现,其实这个求导的目标是相对predict - real残差的。
接下来我们看看其他的损失函数在xgb中怎么使用。
def custom_normal_train( y_pred,dtrain):
label = dtrain.get_label()
residual = (label - y_pred).astype("float")
grad = np.where(residual<0, -2*(residual)/(label+1), -10*2*(residual)/(label+1))#对预估里程低于实际里程的情况加大惩罚
hess = np.where(residual<0, 2/(label+1), 10*2/(label+1))#对预估里程低于实际里程的情况加大惩罚
return grad, hess
上面的是美团做ETA预估的损失函数的改动,大家能看出来他的的前身是什么吗?这个其实是MSE的损失函数,加入的惩罚示例。当残差小于0的时候,也就是真值小于预测值的时候,做了一个特殊的惩罚,这里我们暂时不需要管分母咋有个label,其实只是想都除以一个label+1,做的一个比例值。然后二阶导其实是常数。
回归中的局部惩罚损失函数
在回归任务中,我们可能对某个区间段的错误比较敏感,例如股票预测中,我们不希望将利润大于5%的股票预测成利润小于0的场景,所以需要定义一个区间段的惩罚。
def custom_loss(preds, dtrain):
"""
添加额外惩罚,对真值为负、而预测值为正的情况进行加大惩罚
"""
y_true = dtrain.get_label()
errors = y_true - preds
# 添加额外惩罚,对真值为负、而预测值为正的情况进行加大惩罚
additional_penalty = np.where((y_true < 1) & (preds >= 2.5), 40, 1.0)
gradient = -errors * additional_penalty # 梯度
hessian = np.ones_like(gradient) # 二阶导数
return gradient, hessian
additional_penalty相当于我们在某些区间进行额外惩罚的操作。
分位数回归的损失函数
在回归任务中,有点时候我们还希望做某个分位数的回归,也就是对分布的某一段感兴趣,这个时候就用到了分位数回归的损失函数。
def quantile_loss(preds, dtrain):
"""
分位数损失函数
"""
labels = dtrain.get_label()
quantile = 0.6 # 设置分位数值,可以根据需求调整
errors = labels - preds
mask = errors >= 0
grad = quantile * mask - (1 - quantile) * ~mask
hess = np.ones_like(grad)
return grad, hess
这里需要注意一下,如果你使用了分位数回归的损失函数,如果你评估函数还使用正常的损失函数,你可能会看到越训练损失越大的情况,这个时候需要添加分位数的评估函数。
def custom_eval_metric(preds, dtrain):
"""
分位数评估函数
"""
y_true = dtrain.get_label()
quantile = 0.6 # 设置分位数值,可以根据需求调整
errors = y_true - preds
pinball_loss = np.where(errors >= 0, (quantile - 1) * errors, quantile * errors)
mean_pinball_loss = np.mean(pinball_loss)
return 'pinball_loss', mean_pinball_loss
这样你就能看到正常的训练过程啦。
总结
在使用损失函数的导数的时候,精确的定义是使用一阶导数和二阶导数,但是在使用的时候需要活学活用,找到一个近似的就能够起到一个比较好的效果。