终身学习
什么是终身学习呢? 其实就是当一个模型学会了任务A,当学习任务B的时候不会忘记任务A,这个时候你可能会有个问题,我们重新训练一个模型可以吗? 当然可以,只不过这样的模型比较难维护,天然的场景是对于国际化业务每个城市都要维护一个模型成本也是巨大的。那么解决这样的事情主要有以下三种思路。
- Knowledge Retention 知识记忆。我们不希望学完task1的模型,在学习task2后,在task1上表现糟糕。也就是希望模型有一定的记忆能力,能够在学习新知识时,不要忘记老知识。但同时模型不能因为记忆老知识,而拒绝学习新知识。总之在新老task上都要表现比较好。
- Knowledge Transfer 知识迁移。我们希望学完task1的模型,能够触类旁通,即使不学习task2的情况下,也能够在task2上表现不错。也就是模型要有一定的迁移能力。这个和transfer learning有些类似。
- Model Expansion 模型扩张。一般来说,由于需要学习越来越多的任务,模型参数需要一定的扩张。但我们希望模型参数扩张是有效率的,而不是来一个任务就扩张很多参数。这会导致计算和存储问题。
Knowledge Retention 知识记忆
对于这种方法比较常见的是EWC(Elastic Weight Consolidation)算法,它的核心思想是在损失函数上加入一个正则项,使得模型参数更新必须满足一定条件。
L′(θ)=L(θ)+λi∑bi(θi−θib)2
L(θ)为原始的loss function,后面一项为正则项。
bi为参数更新权重,表示参数θi有多重要,能不能变化太多
θi为需要更新的参数,θib为该参数在之前任务上学到的数值。
bi为参数更新权重,表示参数θi能不能变化太多.
- 如果bi很大,则表明θi不能和θib差距过大,也就是尽量不要动θi
- 如果bi很小,则表明θi的变化,不会对最终loss带来很大的影响。
那么这里有一个关键的问题是,bi怎么能确定呢?EWC给出了它的解决方案。它利用二阶导数来确定bi。如果二阶导数比较小,位于一个平坦的盆地中,则表明参数变化对task影响小,此时bi小。如果二阶导数比较大,位于一个狭小的山谷中,则表明参数变化对task影响大,此时bi大。
这里咱们看几个图就直观啦。
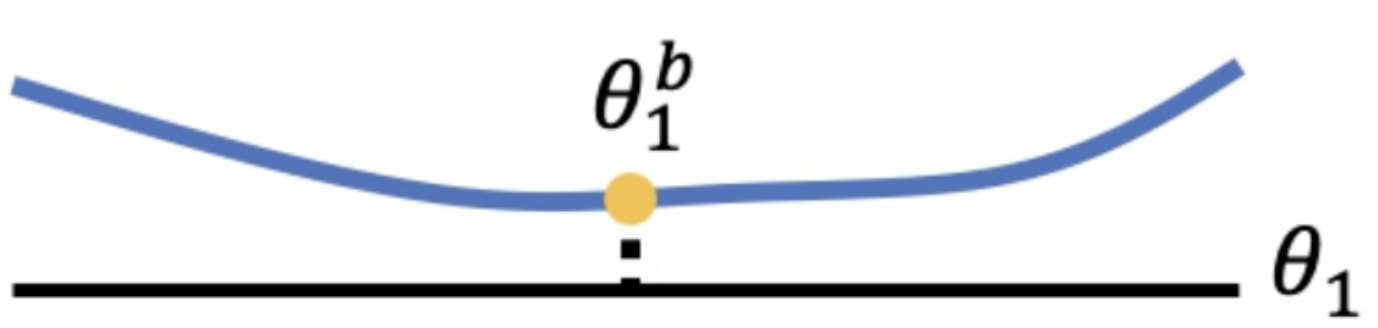
如上图这种情况,其实我们就改动b1影响就不大,但是下图这种形式就不能进行参数更新。
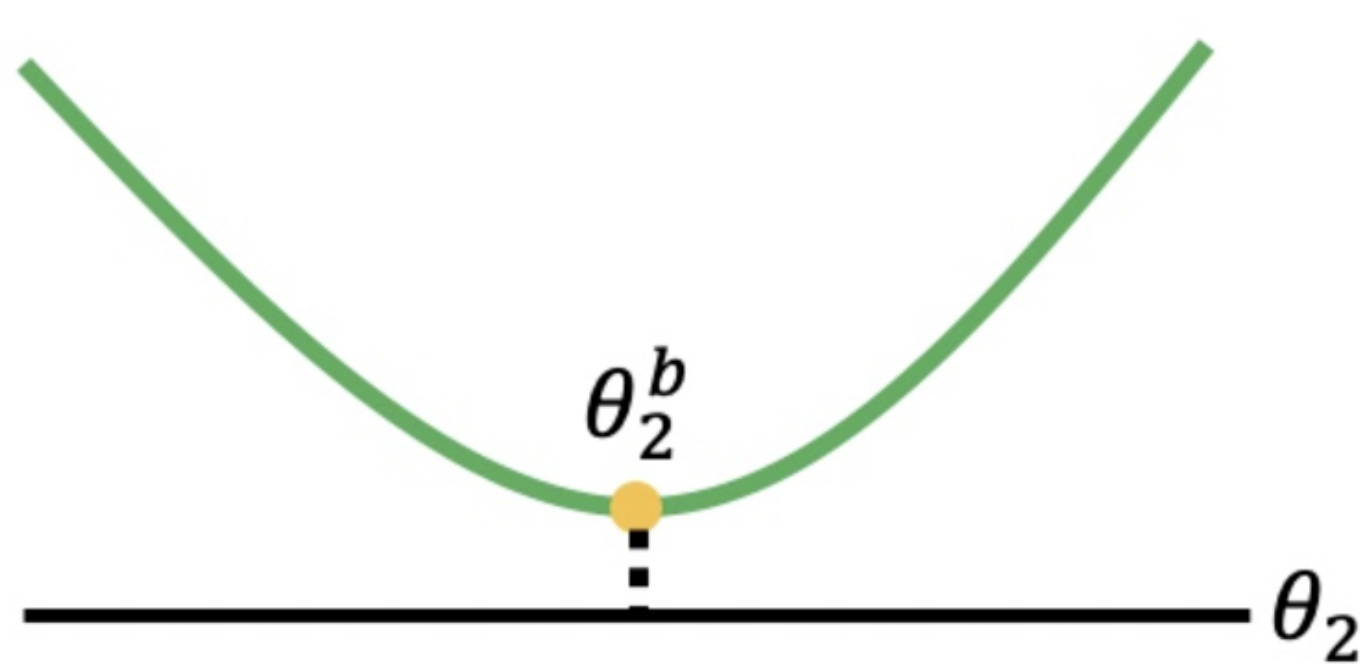
看到这里相信你应该明白了,通过bi的确定,最后我们来确定参数是否更新,随意最后我们更新的参数都是既不影响task1的效果也能让task2效果变好,这也就引进了这个算法的一个致命弱点,如果两个任务相差很大就很难用这种方法更新参数。
Knowledge Transfer 知识迁移
另一个思路解决终身学习的方法是将原来的知识进行迁移,从而防止遗忘,这种方法之前我们在讲元学习的时候是讲过类似的方法,这个一般通过迁移学习实现。
Model Expansion 模型扩张
最后一种方法就是要对模型进行改造,你不是记不住原来的知识吗,我给你增加脑细胞你是不是就能记住了呢?
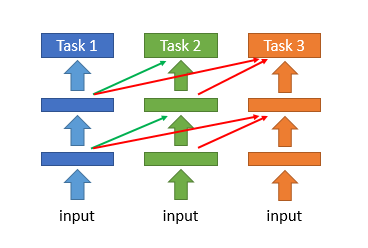
一般来说,由于需要学习越来越多的任务,模型参数需要一定的扩张。但我们希望模型参数扩张是有效率的,而不是来一个任务就扩张很多参数。这会导致计算和存储问题。所以怎么对模型参数进行有效率的扩张,就显得十分关键了。
一种方法是progressive neural network。它将task1每层输出的feature,作为task2对应层的输入,从而让模型在学习后面task的时候,能够记住之前task的一些信息。
网络加宽
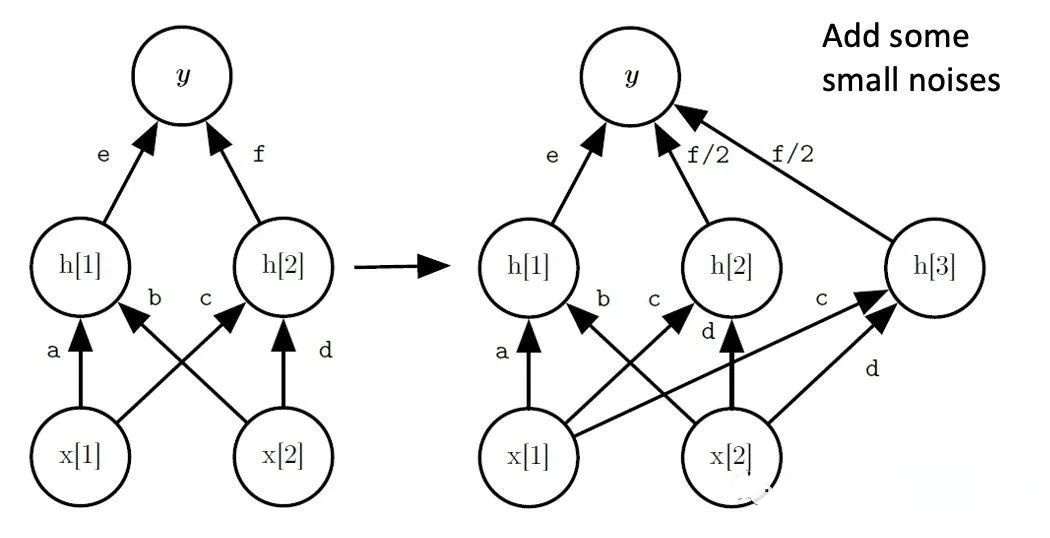
Net2Net。它对网络进行加宽。如下图所示,由神经元h2分裂得到一个神经元h3。初始时和h2一样,h2和h3权重均为之前h2权重的一半。为了防止h2和h3训练过程中始终保持一致,故在h3上添加一些小噪声,使二者能够独立更新。这其实就是知识迁移的方法。
真实场景下的机器学习系统,最终都会变成终身学习系统(Lifelong learning system),不断的有新数据,通过新的数据改善模型,刚开始数据量小,我们使用小的网络,可以防止过拟合并加快训练速度,但是随着数据量的增大,小网络就不足以完成复杂的问题了,这个时候我们就需要在小网络上进行扩展变成一个大网络了。通过不断的更改网络结构使模型一直具备预测各种数据的能力。
评价方法
终身学习的评估方法一定是在不同task之间评估性能。
- ACC
- 记忆能力
- 迁移能力
ACC实际就是所有任务的准确率
记忆能力我们主要想看看学完一个新的任务后,原有任务的性能发生多大的变化
迁移能力是已经学好的模型对没有学习的模型有多少能预测的准。