概率论与数理统计
当你看数据挖掘的相关数据,虽然一遍一遍的看,但是总是不太懂,这个时候你可能需要看看数理统计的相关知识,这是个追根溯源的时代,知识体系也是一样,所以我们开始数学路程吧。
连续随机变量
在生产过程中,我经常面对的是取值是连续的概率分布, 例如身高体重,而在连续随机变量中,我们的频率函数也被密度函数所取代。
∫f(x)dx=1
如果要求(a, b)之间的概率,就可以表示为
∫abf(x)dx=F(b)−F(a)
也就是概率求(a, b)之间的面积。
正态分布
正态分布又称为高斯分布。高斯分布的密度函数如下:
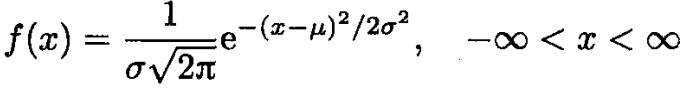
其中μ是均值,σ是标准差。
一般的书中可以表示为 N(\mu,\sigma\^2).
对于一个分布μ=0和σ=1为标准正态分布。
贝塔密度(Beta)
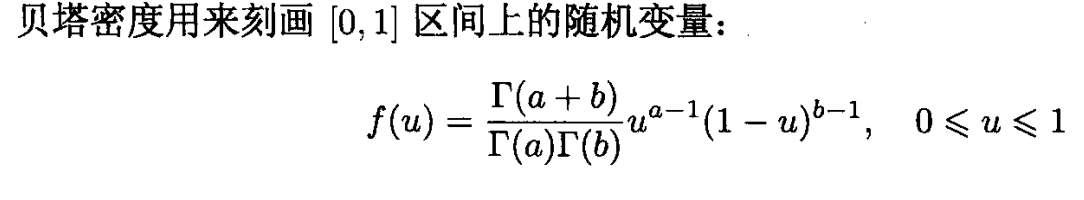
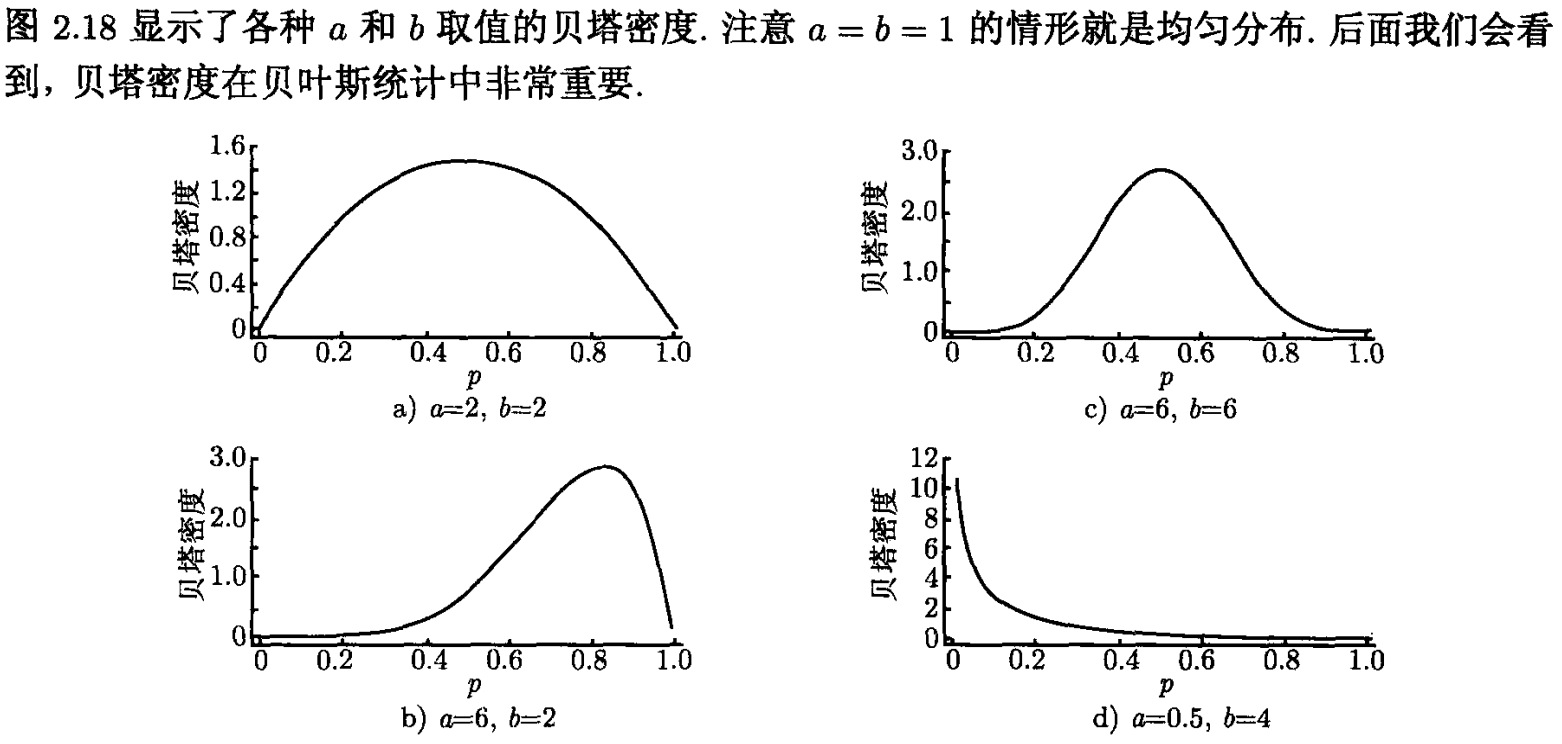
上面就是书本的知识啦,当时截了个图,今天看到做推荐搜索的时候会使用到Thompson sampling,Thompson sampling里会使用到beta分布,一时间也记不起beta分布的概念啦,看了看博客当时果然是偷懒啦,就截图来着。正好这里好好的介绍一下这个beta分布。
beta分布里有两个形状参数,途中是a、b。一般使用‘\alpha,\beta‘表示。然后这个形状参数有一些特性。
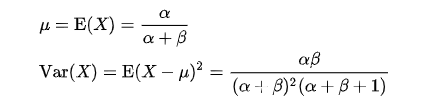
可以通过‘\alpha,\beta‘计算出这个分布的方差。然后来看看一些基本的性质。
共轭先验
共轭先验是指的在贝叶斯学派中,如果先验分布和后验分布属于同类,则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验(Conjugate prior)。
先验分布
贝叶斯学派认为,在我们获得样本结果之前,应该对这个事件有一个认知。在实验之前加入主观判断,可能会取得更好的结果。
后验分布
根据样本的先验分布,再加上实际数据的分布,利用条件概率公式等得到的结果。
似然函数
似然有的时候可能与概率差不多,但是两者的关注点不同。比如我们投硬币,假设这个硬币是质地均匀的公平硬币,连续投两次,都出现正面的概率是0.25;而似然主要关注,都出现了正面的情况下,这枚硬币是否是个公平硬币。当两面都是正面的朝上的似然函数:(其实以结果来看,更偏向于质地不均匀)
对应到上面的例子,咱们来看看一个经典案例。
棒球中的平均击球率是用一个运动员击中棒球的次数除以他总的击球数量,棒球运动员的击球概率一般在0.266左右。假设我们要预测一个运动员在某个赛季的击球率,我们可以计算他以往的击球数据计算平均击球率。但是在赛季刚开始的时候,他击球次数少,因此无法准确预测。比如他只打了一次球,那击球率就是100%或者0。但是显然我们并不会这样预测。
那么怎么使用beta分布拟合棒球运动员真实的击球分布呢?
先验Beta分布
假设所有的运动员击球率在0.27左右,范围一般是0.21到0.35之间。可以用参数α=81和β=219的Beta分布表示。因为当这两个值时,期望是α/(α+β),即0.27;并且分布的主要区间在0.2-0.35之间。
实际数据 二项分布
假设,到目前为止,这个运动员在这个赛季总共打了n次球,击中了x次,这满足二项分布。
后验分布
由于 Beta分布与二项分布共轭先验,由上面的推导可知,后验分布仍然满足Beta分布。结果变成了Beta(α+x,β+(n−x))。
因此,假如我们知道在这个赛季,该运动员打了300次球,击中了100次,那么最终的后验概率为Beta(181, 419)。这样就引入了先验分布后计算得到棒球运动员的实际水平,其实也就是一个结果修正的问题。
那么这个beta分布到底还有有什么用途呢?
在推荐搜索中,topic推荐汇总,经常会用到EE模型,也就是搜索探索模型,是一个典型的强化学习模型,这个时候选择是否出一个topic选项夹就是一个
问题,我们根据历史的动作选出当前情况下应该出一个选项夹的过程,就可以采用beta分布的知识,假设出每种选项夹都是一个beta分布,这个时候需要找到出那个选项夹的转化的概率更大。也称为Thompson Sampling。
切比雪夫不等式
设随机变量X具有数学期望E(X)=μ,方差D(X)=σ2,对于任意ε>0,都有
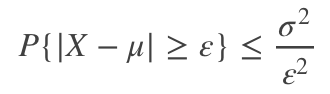
方差越大,X落在区间外的概率越大,X的波动也就越大,与方差的意义统一了。
适用范围
期望、方差都存在的随机变量。
用途
对于随机变量落在期望附近区域内(或外)给出一个界的估计。