概率论与数理统计
当你看数据挖掘的相关数据,虽然一遍一遍的看,但是总是不太懂,这个时候你可能需要看看数理统计的相关知识,这是个追根溯源的时代,知识体系也是一样,所以我们开始数学路程吧。
随机变量
如果随机变量的取值范围是{x1,x2..},且有∑p(x)=1的函数p,我们称这个函数是随机变量x的概率质量函数或是频率函数。有时候利用随机变量的累计分布函数比较方便。
F(x)=P(X<x)
伯努利随机变量
伯努利随机变量仅仅取两个值,分别是0和1,各自的概率我p和1-p,因此它的频率函数为
p(1)=p
p(0)=1−p
p(x)=0
一种比较熟悉的表达是
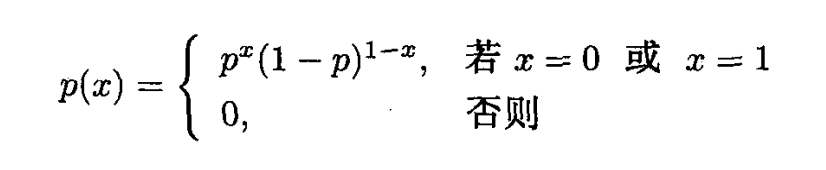
###二项分布
假设进行n次伯努利实验,k次成功的概率为:
p(k)=C(n,k)pk(1−p){n−k}
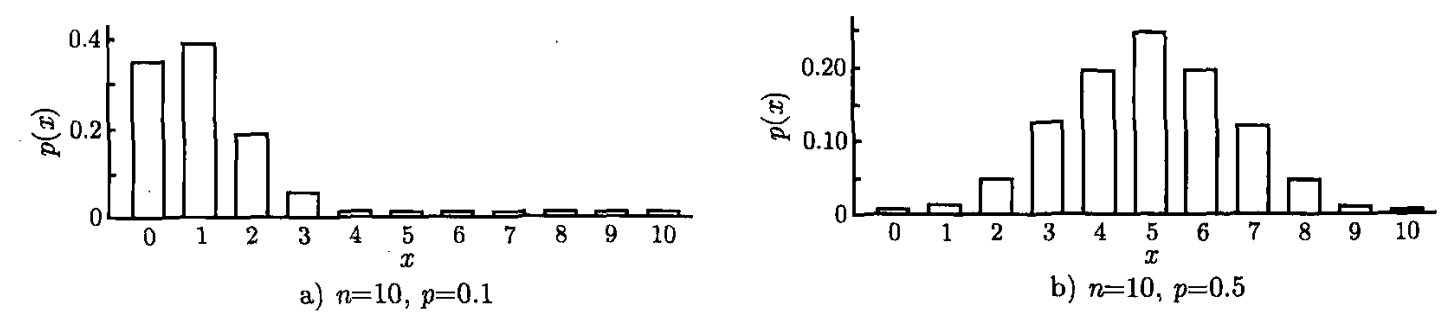
以上就是随着p的变化,二项分布的频率函数。
几何分布
几何分布也是由多个独立的伯努利实验构成的,但是是无穷次的实验序列构成,每次成功的概率是p,直到第一次成功所做的实验次数,因此当X=k时,实验成功,前k-1次全部失败,则集合分布的发生概率为:
p(k)=(1−p){k−1}p
需要注意的是,这些独立实验的概率和也是1
P=∑(1−p)jp=1
超几何分布
超几何分布假设盒里有n个球,r个黑球和n-r个白球,从盒里无重复的抽取m个球,X表示抽到黑球的个数。
$$
X=\frac{(r,k)(n-r,m-k)}{(n,m)}
$$
泊松分布
参数为λ的频率函数是:
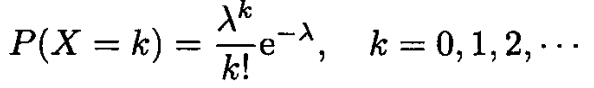
随着参数的变化,泊松分布的变化如下图。