概率论与数理统计

当你看数据挖掘的相关数据，虽然一遍一遍的看，但是总是不太懂，这个时候你可能需要看看数理统计的相关知识，这是个追根溯源的时代，知识体系也是一样，所以我们开始数学路程吧。本节我们要学一学经常被提到且常用的分布，算是积攒经验了，后面很多机器学习数学建模都是基于现在的本钱，所以咱们来开始学习吧。

卡方分布

设 $X_1,X_2,......X_n$相互独立, 都服从标准正态分布N(0,1), 则称随机变量$\chi^2=X1^2+X2^2+...+Xn^2$所服从的分布为自由度为 n 的χ2分布

卡方分布的期望是和方差分别是：

E（χ2）=n，方差D(χ2)=2n

$\chi^{2}$分布有两个主要用途：

（1）用于检验拟合优度，也就是可以检验一组数据与指定曲线的拟合程度，或检验某组观察值是否符合某种分布。

（2）检验两个变量的独立性，通过这个方法检查两个变量之间是否存在某种关联

拟合优度检验

我从网上找到一个比较好的例子，来说明这一用途。

开发了一台体重秤，我想通过与标准体重秤对比，看看我开发的体重秤在精度上是否能够和标准设备相媲美，是否与标准设备存在显著差异，于是我找来5个人，我知道他们总体重值为300kg，所以我只需要知道4个人的体重，就可以知道第五个人的体重，因此，确定了自由度为4，然后设定了显著性水平=0.05。对于每一个人，各用我开发的体重秤和标准体重秤称量一次，我就获得了每个人的期望值（标准称量结果）与我的观察值（我开发的体重秤称量结果），然后带入卡方公式求得卡方值，与查表所得临界值进行比较，如果大于临界值，说明差异显著。

变量独立性检验

与拟合优度检验的差别在于需要通过观察值算出期望值，这要依靠概率。。。 首先要为两个变量构建列联表，假设我们要检验一场赌局的结果是否与庄家有关系

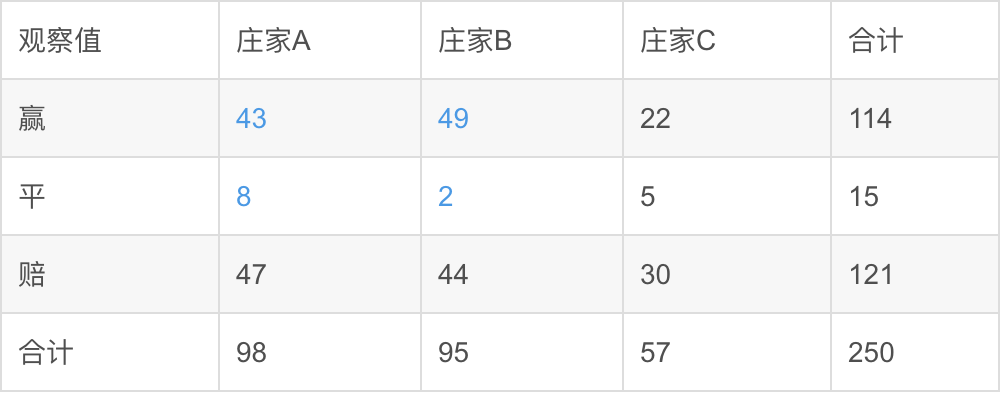
据此依靠概率建立期望值，我们假设庄家和是否赢局无关，则依据此假设建立起来的A坐庄且赢的概率=A坐庄率X赢局率

A坐庄率=98/250

赢局率 =114/250

于是与A坐庄且赢的观察值所对应的期望值为250XA坐庄率X赢局率
以此类推，可求得其他期望值。

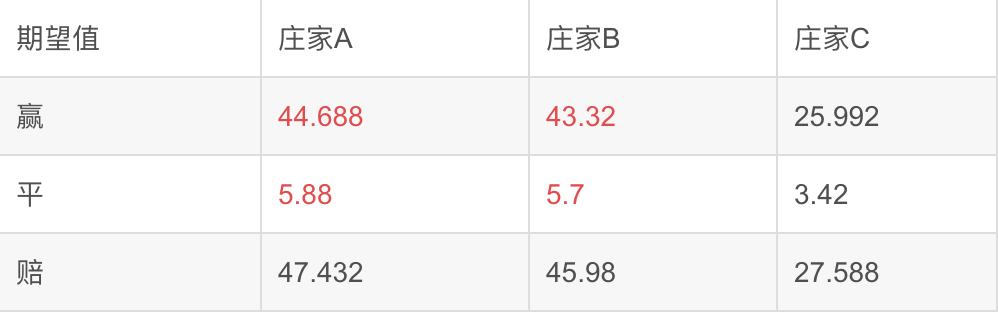
自由度是在考虑限制条件的情况下，可以自由选择的独立信息的数目。鉴于我们知道每一行和每一列的总和，因此，只需知道表中红色部分的内容即可，因此自由度为4.

当卡方结果大于临界值，说明观察值和期望值有差别，由于我们的假设认为是否赢局和庄家没有关系，基于此假设，计算得到期望值，可实际观察值和期望值却有明显差别，则说明两个变量不独立，反之，如果卡方结果小于临界值，则独立。

就是因为我们在假设两个变量相互独立的情况下得到的期望值，如果观察值与期望值无显著差别，说明观察值符合我们的假设。

卡方分布随着自由度变化的图像

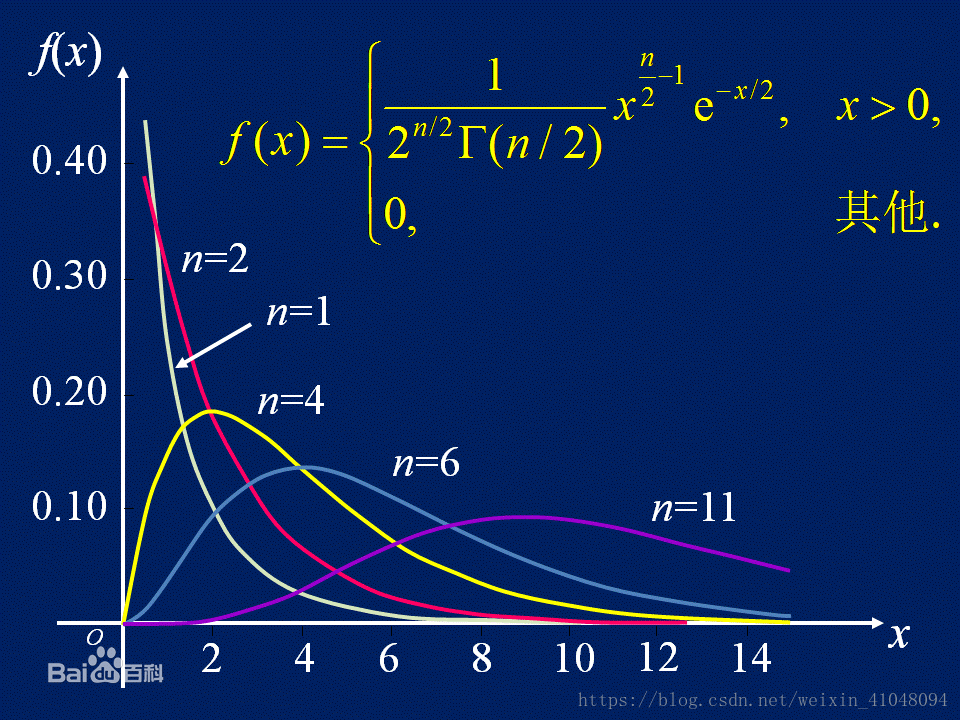
卡方公式

假设有两个分类变量X和Y，它们的值域分别为{x1, x2}和{y1, y2}，其样本频数列联表为：

若要推断的论述为H1：“X与Y有关系”，可以利用独立性检验来考察两个变量是否有关系，并且能较精确地给出这种判断的可靠程度。

\chi\^2=\frac\{(ad-bc)2*n\}\{(a+b)(c+d)(a+c)(b+d)\}

自由度v=(行数-1)(列数-1)

要求样本含量应大于40且每个格子中的理论频数不应小于5。当样本含量大于40但理论频数有小于5的情况时卡方值需要校正，当样本含量小于40时只能用确切概率法计算概率

t分布

“t”，是伟大的Fisher为之取的名字。Fisher最早将这一分布命名为“Student’s distribution”，并以“t”为之标记。

t分布常常用于根据小样本来估计呈正态分布且方差值未知的样本的均值。（如果总体的方差已知的话，则应该用正态分布来估计总体的均值。）(所以一个前提是：t分布的样本的总体必须符合正态分布)

t分布一般用于小样本(样本量比较小)的情形。

假设X服从标准正态分布即X_{N(0,1)，Y服从自由度n的卡方分布即Y}χ2（n），且X与Y是相互独立的，那么Z=X/sqrt(Y/n)的分布成为自由的为n的t分布，记为Z~t(n).

对于Z~t(n)，其数学期望E(Z) = 0，n>1;方差D(Z)=n/n-2 , n>2 。

特征

以0为中心，左右对称的单峰分布；

t分布是一簇曲线，其形态变化与n（即其自由度）大小有关。自由度n越小，t分布曲线越低平；自由度n越大，t分布曲线越接近标准正态分布（u分布）曲线，当自由度无限大时，t分布就成了正态分布

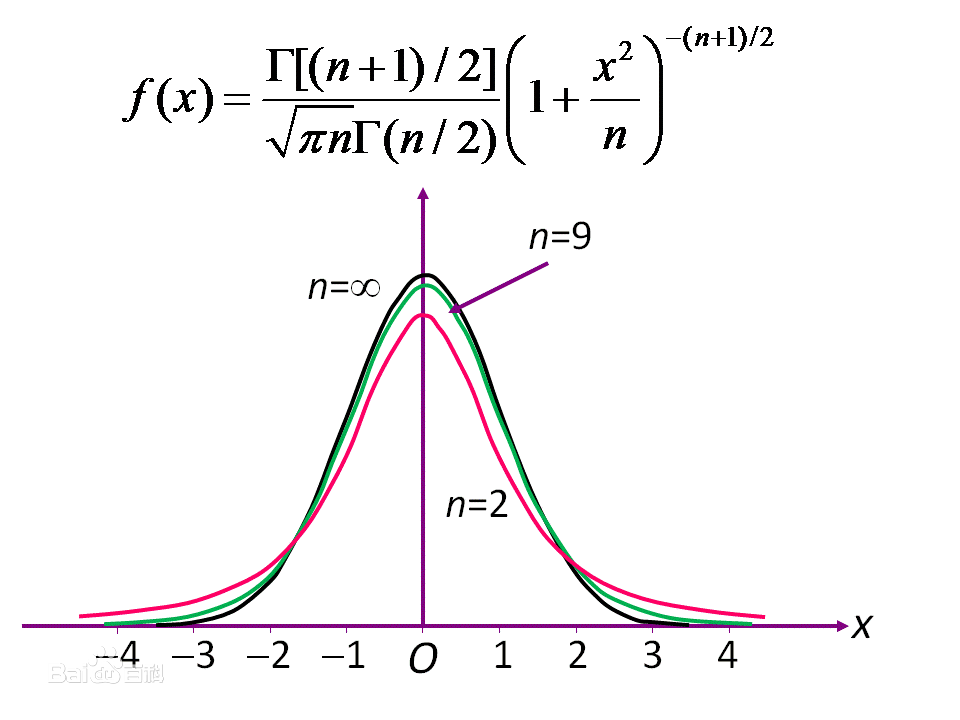
.随着自由度逐渐增大，t分布逐渐接近标准正态分布。

注意：
在概率论和统计学中，t-分布 经常应用在 对正态分布的总体的均值 进行估计。t检验改进了Z检验，不论样本数量大或小皆可应用。在样本数量大(超过120)时，可以应用Z检验，但Z检验用在小的样本会产生很大的误差，因此样本很小的情况下得改用t检验。

F分布

设X1服从自由度为m的χ2分布,X2服从自由度为n的χ2分布，且X1、X2相互独立，则称变量$F=\frac\{X1/m\}\{X_2/n\}$所服从的分布为F分布，其中第一自由度为m,第二自由度为n.

特征

1.期望E(F)=n/(n-2)，方差$D(F)=2n^2(m+n-2)/m(n-2)^2(n-4)$

2.若F_{F(m,n)，则1/F}F(n,m)

3.若F_F(1,n)，TT(n)，则F=T\^2