多层感知机

​ 首先我们来介绍多层感知机，其实根据字面的意思我们已经能够了解大半，就是将一个简单的感知机进行连接，其中层数可以任意挑选，中的维度都可以任意挑选。它的样式是这样的。

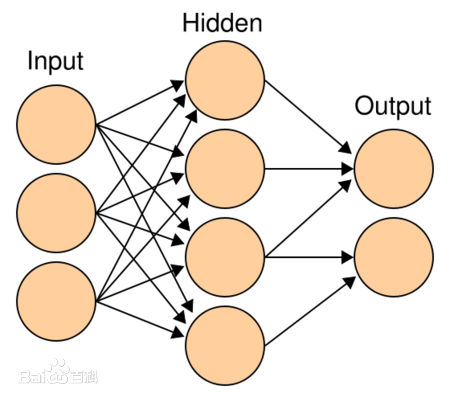
结构比较简单，输入层进来以后就和隐藏层进行权重转换，直到输出层。它的激活函数不是我们在我们的系统上搜索[感知机]

的文章中提到的示例函数，一般采用sigmod或者是tahn激活函数，因为激活函数在本文是需要求导的，所以选择的时候要相对比较小心，示例函数不是左右的定义域都是可导的，这个也是本文算法的一个改进。

BP算法

我们开始进入正题，首先我们简单了解下BP算法的求导过程。

$$x_{j}^{l}=\sum_{k}w_{ji}^{l}y_{i}^{l-1}+ \theta_{j}^{i} \tag{1.1}$$

$$y_{j}^{l}=f(x_{j}^{l})\tag{1.2}$$

$w_{ji}^{l}$表示第l-1层的第i个参数，$x_{j}^{l}$表示第l层的第j个神经元输入，$y_{j}^{l}$是第l层的第j个神经元的输出，$\theta$表示相应的偏置，$f(.)$表示激活函数。

损失函数

$$C=\frac{1}{2}||Y-y^{l}||^2 \tag{1.3}$$

其中$Y$表示标签，$y^{l}$表示神经网络的最后一层输出，C就是损失其实就是拟合程度。

接下来就是我们如何调整中间的权重让损失最小的过程。我们来定义每一层的损失$\delta$,$\delta_{j}^{l}$表示第l层第j个神经元的损失。

$$\delta_{j}^{l}=\frac{\partial C}{\partial x_{j}^{l}} \tag{1.4}$$

集合公式1.1和1.2,

$$\delta_{j}^{l}=\frac{\partial C}{\partial y_{j}^{l}} f^{'}(x_{j}^{l}) \tag{1.5}$$

因为前一次神经元的输出是后一层神经元的输入，

$$\delta_{j}^{l}=\frac{\partial C}{\partial x_{j}^{l}}=\sum \frac{\partial C}{\partial x_{i}^{l+1}} \frac{\partial x_{i}^{l+1}}{\partial x_{i}^{l}}=\sum \frac{\partial x_{i}^{l+1}}{\partial x_{i}^{l}} \delta_{i}^{l+1} \tag{1.6}$$

在公式1.6中$x_{i}^{l+1}$是$x_{i}^{l}$的函数，所以

$$x_{i}^{l+1}=\sum_{j} w_{ij}^{l+1}y_{j}^{l}+\theta_{i}^{l+1}=\sum w_{ij}^{l+1}f(x_{j}^{l}) + \theta_{i}^{l+1} \tag{1.7}$$

对上面公式的$x_{j}^{i}$求导

$$\frac{\partial x_{k}^{l+1}}{\partial x_{j}^{l}}=w_{ij}^{l+1} f'(x_{j}^{l}) \tag{1.8}$$

$$\delta^{l}_{j}=\sum w_{ij}^{l+1}\delta^{l+1}_{j}f'(x_{j}^{l}) \tag{1.9}$$

以上求导的过程就是反向传播的过程。权重更新通过公式1.10

$$x_{j}^{l+1}=\sum w_{ij}^{l}y_{i}^{l-1} + \theta \tag{1.10}$$

那么

$$\frac{\partial C}{\partial w_{ji}^{l}}=\frac{\partial C}{\partial x_{j}^{l}} \frac{\partial x_{j}^{l}}{\partial w_{ji}^{l}}=\delta_{j}^{l}y_{i}^{l-1} \tag{1.11}$$

$$\frac{\partial C}{\partial \theta_{j}^{l}}=\frac{\partial C}{\partial x_{j}^{l}} \frac{\partial x_{j}^{l}}{\partial \theta_{ji}^{l}}=\delta_{j}^{l} \tag{1.12}$$

梯度更新法则为

$$w_{ji}^{l}=w_{ji}^{l}-\alpha \frac{\partial C}{\partial w_{ji}^{l}}=w_{ji}^{l}-\alpha \delta_{j}^{l} y^{l-1}_{i} \tag{1.13}$$

$$\theta_{j}^{l}=\theta_{j}^{l}-\alpha \frac{\partial C}{\partial \theta_{j}^{l}}=\theta_{j}^{l}-\alpha \delta_{j}^{l} \tag{1.14}$$

简单实现

import numpy as np

n = 0
lr = 0.05

X = np.array([
    [1, 1, 2, 3],
    [1, 1, 4, 5],
    [1, 1, 1, 1],
    [1, 1, 5, 3],
    [1, 1, 0, 1]])
Y = np.array([1, 1, -1, 1, -1])

W = (np.random.random(X.shape[1]) - 0.5) * 2


def get_update():
    global X, Y, W, lr, n
    n += 1
    new_out = np.dot(X, W.T)
    new_W = W + lr * (Y - new_out.T).dot(X) / int(X.shape[0])
    W = new_W


def main():
    for _ in range(1000):
        get_update()
        print np.dot(X, W.T)
    last_output = np.dot(X, W.T)
    print last_output

if __name__ == '__main__':
    main()

关键的一行就是第21行的权重更新，本文只是实现一个非常简单的神经网络，仅供学习使用，希望大家能了解这个里面的原理。