激活函数

我们在感知机和BP算法中都提到了激活函数这一个概念，在神经网络一文中也提到这一个概念，我们通过隐藏层来的转换是对原始数据进行线性的转换，例如拉伸和缩小旋转，只有通过非线性的激活函数才能将原始和数据进行扭曲等的操作，既然激活函数这么好，那么我们都有哪些激活函数呢，激活函数之间有什么可以选择的空间吗？

sigmod函数

这个是比较常用的激活函数。

$$f(x)=\frac{1}{1+e^{-x}} \tag{1.1}$$

sigmod的函数。左边是原始函数图像，右边是导数图像。

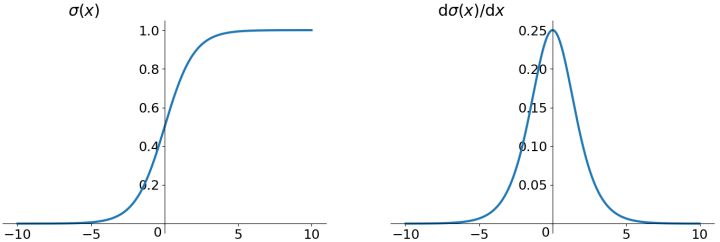
我们能够容易发现几个特点，在值域y上始终为正的。

优点

1. 便于求导
2. 平滑
3. 可以作为概率，辅助模型解释

缺点

1. 幂运算相对耗时
2. 导数值小于 1，反向传播易导致梯度消失（Gradient Vanishing）
3. 输出值不以零为中心，可能导致模型收敛速度慢

其他几个缺点比较容易理解，但是这个缺点3是为什么呢？为什么非的以零为中心收敛就不会慢呢？

我们想通过数学的方式来解释这一点。

这里首先需要给收敛速度做一个诠释。模型的最优解即是模型参数的最优解。通过逐轮迭代，模型参数会被更新到接近其最优解。这一过程中，迭代轮次多，则我们说模型收敛速度慢；反之，迭代轮次少，则我们说模型收敛速度快。

参数更新

首先我们要从参数更新的的角度来考虑这个问题，如果对参数更新有问题，我们可以参考本站的[BP算法]的内容。

$$w = w -\alpha \frac{\partial C}{\partial w} \tag{1.2}$$

其中$C$是损失函数，$w$是学出来的参数。对于$\alpha$是学习率，也就是超参数，我们不会更改太多，那么核心就是计算$\frac{\partial C}{\partial w}$，然后我们考虑，对于某个神经元来说。

$$f(x;w,b)=f(z)=f(\sum w_i x_i +b) \tag{1.3}$$

而对于参数$w_i$来说

$$\frac{\partial C}{\partial w}=\frac{\partial C}{\partial f} \frac{\partial f}{\partial z} \frac{\partial z}{\partial w}=x_i \frac{\partial C}{\partial f} \frac{\partial f}{\partial z} \tag{1.4}$$

$$w_i = w_i - \alpha x_i \frac{\partial C}{\partial f} \frac{\partial f}{\partial z} \tag{1.5}$$

从公式1.4 1.5能够看出，$w_i$的实际更新方向实际上是由$x_i \frac{\partial C}{\partial f} \frac{\partial f}{\partial z}$决定的，而$\frac{\partial C}{\partial f} \frac{\partial f}{\partial z}$是导数，而sigmod的导数恒为正，所以$\frac{\partial C}{\partial f} \frac{\partial f}{\partial z}$也是正的。所以梯度的方向完全取决于输入$x_i$的符号。

举个栗子

$$f(x;w,b)=f(w_0x_0+w_1x_1+b)$$

参数$w$的值与最优解有如下关系。

\begin{equation} f(\boldsymbol{x}) =\left\{ \begin{array}{ll} w_0<w_{0}^{*} \\ w_{1} >=w_{1}^{*} \end{array}\right. \end{equation}

这也就是说，我们希望 $𝑤_0$ 适当增大，但希望 $w_1$ 适当减小。考虑到上一小节提到的更新方向的问题，这就必然要求 $x_0$ 和 $x_1$ 符号相反,而$x$是输入数据，我们不让让他们符号相反。但是这个时候为了模型收敛，只能如下图一样。

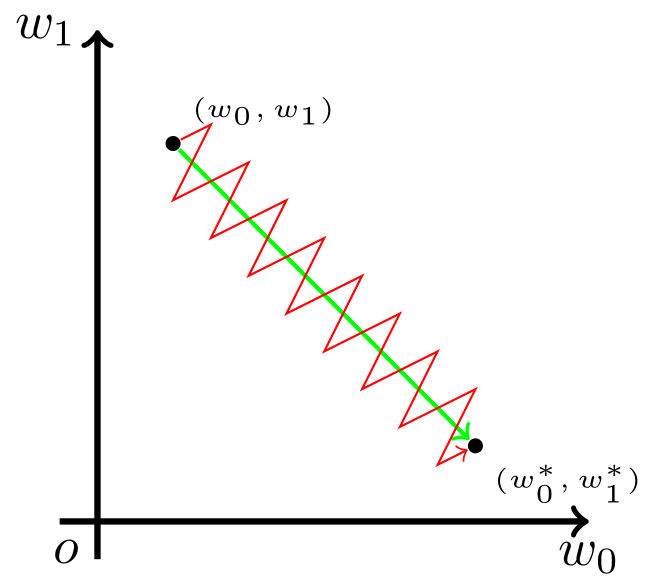
如图，模型参数走绿色箭头能够最快收敛，但由于输入值的符号总是为正，所以模型参数可能走类似红色折线的箭头。如此一来，使用 Sigmoid 函数作为激活函数的神经网络，收敛速度就会慢上不少了。

Softmax函数

顺势可以提一下Softmax函数，这个函数是sigmod的多分类形式，具体计算方式如下。

$$SoftMax(x_{i})=\frac{e^{x_{i}}}{\sum_{j=1}^{K} e^{x_{j}}}$$

下面说一个这个函数的问题，当$x_{i}$是一个很大的值|c|的情况下，分子就会溢出，这个时候叫做上溢，另一种情况是当|c|很大，但是c是一个负数的时候，就会造成下溢的问题。

上下溢解决办法

引入一个$M=max(x_{i})$, 然后计算$SoftMax(x_{i})$的值就能解决上溢的问题，这个时候你会发现结果值是不变的。这个叫做softmax的冗余性。

下溢解决办法

此时分母是一个极小的正数，有可能四舍五入为0的情况。这个时候再去计算log，相当于计算log(0)。是一个无穷的值，这个时候就是下溢的问题。 这个时候看看咱们之前的方法是否能解决这个问题，在用梯度下降法最小化交叉熵损失函数的时候，对参数求导需要计算log(softmax)。这个时候如果softmax的结果为0，那么就会出现下溢的问题， 用这个方法同样可以保证不会出现log(0)的情况，因为softmax的分母至少有一项为1，就不会等于0了。

$$log()=\frac{e^{x-M}}{\sum_{i=1}^{K}e^{x^{i}-M}}\\ =log(e^{x-M})-log(\sum_{i=1}^{K}e^{x_{i}-M}) \\ =(x-M)-log(\sum_{i=1}^{K}e^{x_{i}-M})$$

这种情况下，即使$x_{i}=M$，可见用这个方法同样可以保证不会出现log(0)的情况，因为softmax的分母至少有一项为1，就不会等于0了。

tanh函数

$$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \tag{1.6}$$

tanh的函数表达如公式1.6描述的一样。

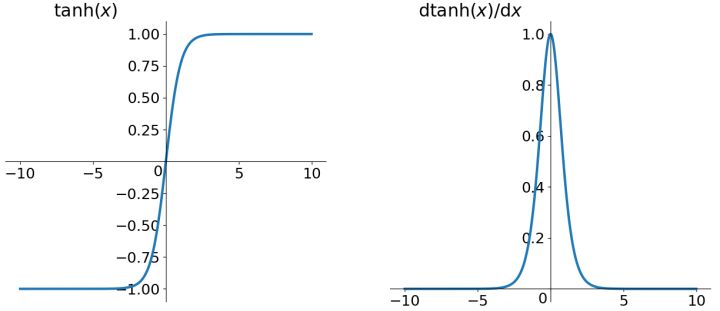
根据上面的讲解，我们发现tanh函数解决了不以零为中心的问题，但是梯度消失和幂运算的问题仍然存在。

ReLU函数

$$f(x)=max{0,x} \tag{1.7}$$

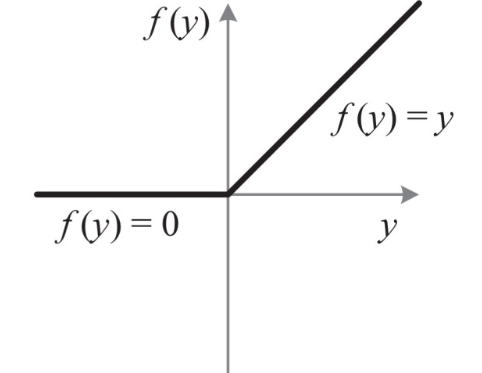
经过上面的讲解，其实Relu函数是解决了上面提到的梯度消失的问题，而且计算速度很快，只需要判断是否大于0就可以。收敛速度远远快于上面提到的激活函数，但是Relu函数仍然不是零均值的输出分布。并且存在Dead Relu Problem，就是传说中的某些神经元永远不会参与计算，导致相应的参数无法更新。会有如下两个原因导致这个问题，从而导致训练过程中参数更新过大。解决办法是使用Xavier初始化方法，以及避免使用较大的学习率，或者使用Adagrad等自动调节学习率算法。

1. 参数初始化
2. 学习率过高

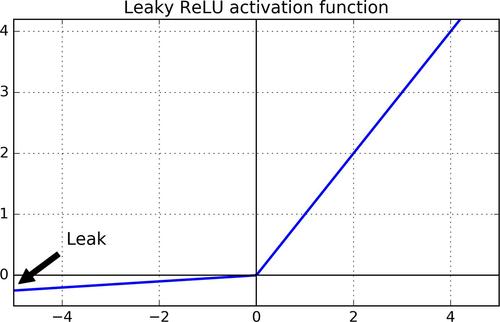
leaky ReLU

leaky ReLU是专门为了解决RuLU中的Dead ReLU的问题，将ReLU的前半段设置成$0.01x$,而非0。理论上Leaky ReLU 继承ReLU的所有优点，并且还没有Dead ReLU的问题。

$$f(x)=max{0.01x,x} \tag{1.8}$$

指数线性单元ELU

\begin{equation} f(\boldsymbol{x}) =\left\{ \begin{array}{ll} \alpha (e^x - 1), & x<=0 \\ x, & x>0 \end{array}\right. \end{equation}

指数线性单元能够使神经元平均激活均值趋于0，对噪声更具有鲁棒性，但是计算量较大。

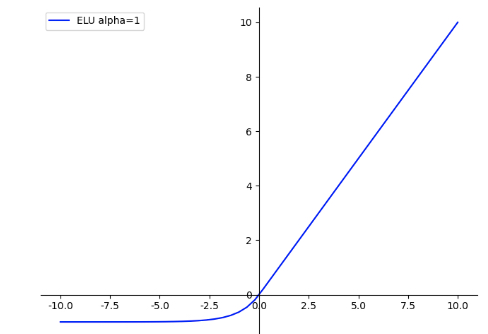
$$ELU=max(0,x)+min(0,r(exp(x)-1))$$

1. ELU具有Relu的大多数优点，不存在Dead Relu问题，输出的均值也接近为0值；
2. 该函数通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向0加速学习；
3. 该函数在负数域存在饱和区域，从而对噪声具有一定的鲁棒性；

饱和

当我们的x趋近于正无穷，h（x）'趋近于0，那么我们称之为右饱和。
当我们的n趋近于负无穷，h（x）'趋近于0，那么我们称之为左饱和。
当一个函数既满足左饱和又满足右饱和的时候我们就称之为饱和。

SELU

\begin{equation} f(\boldsymbol{x}) =\lambda \left\{ \begin{array}{ll} \alpha (e^x - 1)& x<=0 \\ x, & x>0 \end{array}\right. \end{equation}

其实就是ELU乘了个lambda，关键在于这个lambda是大于1的。以前relu，prelu，elu这些激活函数，都是在负半轴坡度平缓，这样在activation的方差过大的时候可以让它减小，防止了梯度爆炸，但是正半轴坡度简单的设成了1。而selu的正半轴大于1，在方差过小的的时候可以让它增大，同时防止了梯度消失。这样激活函数就有一个不动点，网络深了以后每一层的输出都是均值为0方差为1。
当其中参数取为$\lambda=1.0507, \alpha=1.6733$时，在网络权重服从标准正态分布的条件下，各层输出的分布会向标准正态分布靠拢。这种「自我标准化」的特性可以避免梯度消失和爆炸的问题，让结构简单的前馈神经网络获得甚至超越 state-of-the-art 的性能。

自归一化神经网络中提出只需要把激活函数换成SELU就能使的数据经过几层转换以后变成一个固定分布。