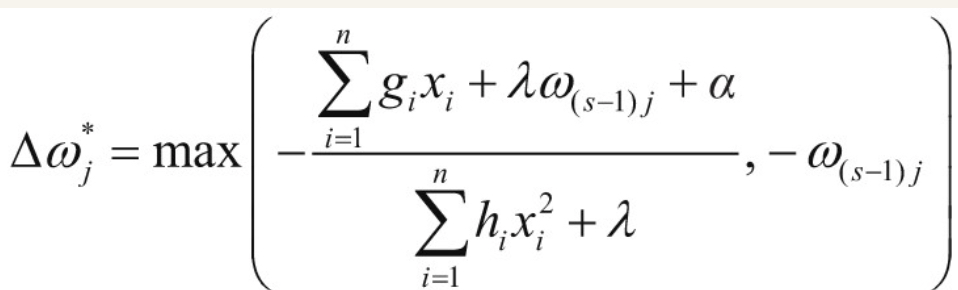XGBoost不仅实现了以CART为基础的树模型，还实现了一个以Elastic Net和并行坐标下降为基础的线性模型，此时XGBoost相当于一个同时带有L1正则和L2正则的逻辑回归（分类问题）或者线性回归（回归问题）。通过对前面章节的学习，我们对XGBoost的树模型有了一个比较深入的理解。本节将介绍XGBoost线性模型的实现原理。

Elastic Net回归

在统计学模型中，回归分析是评估变量间关系的统计过程。它可以衡量变量之间的相关性，常被应用于预测分析、时间序列模型及发现变量的因果关系。例如，房价面积及其价格预测就是很经典的回归问题。回归分析作为建模和分析工具主要有如下优势：
1）可以衡量自变量与因变量之间的显著关系；
2）可以衡量多个自变量对一个因变量的影响强度

回归分析有多种很多实现方法，包括线性回归、逻辑回归。XGBoost线性模型采用的回归方式Elastic Net。为了更好地理解Elastic Net回归，我们首先介绍岭回归（ridge regression）和套索回归（lasso regression）。

岭回归

岭回归是一种用于多重共线性（自变量高度相关）数据的回归技术。它实际是一种改良版的最小二乘法，可避免最小二乘法因为某些噪声数据产生过拟合。岭回归在标准最小二乘平方误差的基础上增加了正则项

$$J(w)=\sum_{i=0}^{i=m}(y^{i}-w^{T}x^{i})^2+\lambda \sum_{j=1}^{n}w_{j}^{2}$$

公式中的正则项就是L2正则项。岭回归通过L2正则项惩罚不重要特征的参数ω实现防止模型过拟合，提高泛化能力。

套索回归

套索回归和岭回归类似，只不过套索回归采用了L1正则而非L2正则。L1的惩罚函数采用了绝对值，这样会导致一些参数趋向于0，相当于从n个变量中进行了变量选择。

$$J(w)=\sum_{i=0}^{i=m}(y^{i}-w^{T}x^{i})^2+\lambda \sum_{j=1}^{n}|w_{j}|$$

3.Elastic Net回归

套索回归虽然可以使参数稀疏化（将一些参数收缩为0），但是它也存在一些限制：如果p>n，即变量维度大于样本量，则套索回归最多只能选择出n个变量，选择的特征数量受限于样本量；对于分组变量，套索回归只能选择其中一个变量而忽略其他变量。Elastic Net回归解决了这些限制，它在套索回归的基础上增加了L2正则。L2正则使得损失函数成为严格凸函数，因此它拥有唯一的最小值。Elastic Net回归同时结合了岭回归L1正则和套索回归L2正则，具备了岭回归和套索回归的双重特点。Elastic Net回归通过lambda1和lambda2两个参数来平衡两种正则项的组合。

$$J(w)=\sum_{i=0}^{i=m}(y^{i}-w^{T}x^{i})^2+\lambda_{2} \sum_{j=1}^{n}|w_{j}|+\lambda_{1} \sum_{j=1}^{n}w_{j}^{2}$$

坐标下降法

坐标下降法（coordinate descent method）是大数据优化领域经典的优化算法。坐标下降法的策略是在每一轮迭代过程中进行单个坐标（每个特征可看作一个坐标）方向的更新，即在当前点处沿着一个坐标方向进行一维搜索，直到找到函数的局部极小值，然后按此方法循环遍历其他不同坐标，直至函数收敛。坐标下降法的执行步骤如下。
1）选择一个初始参数向量ω。
2）固定迭代轮数或者直至模型收敛：

①从1～n中选择一个索引i；
②选择步长α。
③更新$ω_{i}$为

$$w_{i}-\alpha \frac{\partial}{w_{i}}(w)$$

坐标下降法和梯度下降法的主要区别是下降方向的选取。坐标下降法是每次沿一个坐标方向进行更新，而梯度下降法则是每次沿一个梯度方向进行更新。相比于梯度下降，坐标下降通常在一轮迭代中需要更少的内存，具有良好的可用性和可扩展性，但坐标下降比梯度下降需要更多的迭代轮数才能达到收敛。

XGBoost线性模型的实现

Elastic Net回归和并行坐标下降法，它们是XGBoost线性模型实现的基础.
XGBoost线性模型的目标函数定义为.

$$obj=\frac{1}{n} \sum_{0}^{n}L(y^{i}, y^{'})+ \Omega(w,b) \tag{1.1}$$

$y^{i}$为第i个样本在模型s轮时得到的预测值；$y^{'}$为第i个样本的真实值；L为损失函数；Ω为正则化项。
其中

$$\Omega(w,b)=\frac{1}{2}\lambda ||w||^{2} + \frac{1}{2} \lambda_{b}b^{2}+\alpha ||w||_1$$

m为特征的数量；λ为L2正则项对参数ω的系数；$λ_{b}$为L2正则对偏移量b的系数；α为L1正则项的系数。正则化项Ω由L1正则项和L2正则项两项组成，这符合Elastic Net回归的定义.

梯度计算

因为向量乘积满足分配率，所以可以对线性模型的参数进行如下改写：

$$w_{s}^{t} x+b_{s}=(w_{s-1}^{t}+△w^{t})x+b_{s-1}+△b$$

式中，$ω_{s}$为第s轮训练时的参数；$ω_{s-1}$为s-1轮的参数；△ω为两轮训练中ω的变化；$b_{s}$、$b_{s-1}$分别第s轮和第s-1轮训练时的偏移；△b为两轮训练中b的变化。由此，式1.1可以写为

$$obj^{s}=\frac{1}{n} \sum_{0}^{n}L(y^{i}, y^{'(s-1)}+△wx_{i}+△b)+ \Omega(w,b) \tag{1.1}$$

和XGBoost树模型一样，可以对线性模型公式进行泰勒展开：

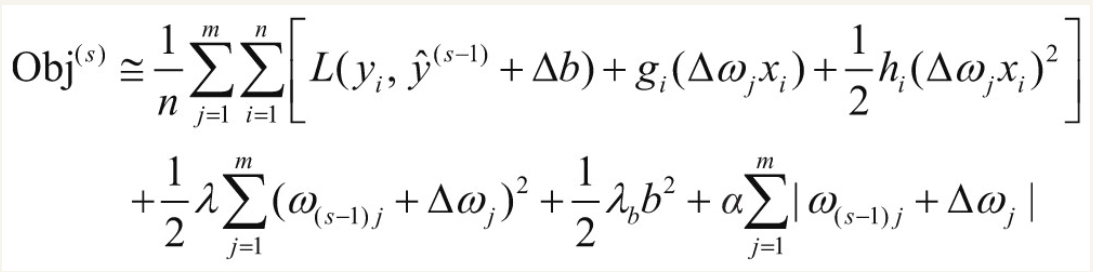
为了简化问题，暂时只考虑L2正则项，去掉L1正则项和常数项，上述公式整理可得

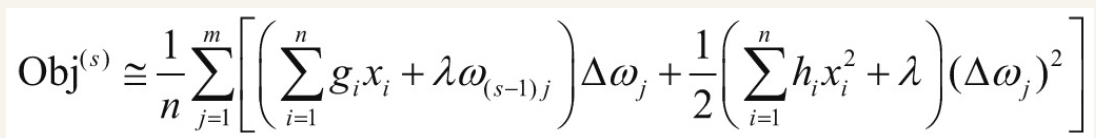
此时目标函数相当于一个以△ω_{j}为自变量的一元二次函数，根据一元二次函数最值公式，可以得到△ω_{j}最优值：

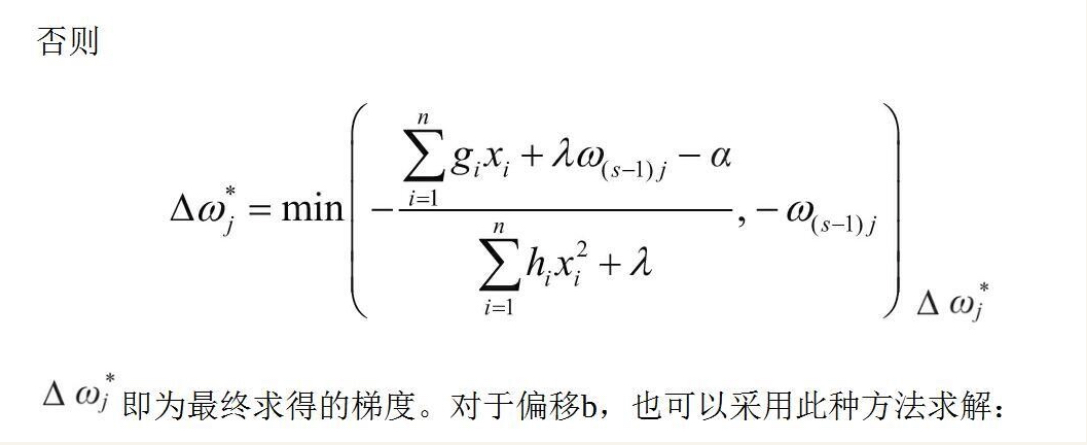
此时重新引入L1正则项，首先判断ω_{(s-1)}_j+△ω_{j}$与0的大小关系。如果ω_{(s-1)}_{j}+△ω_{j}≥0，则