卷积
CNN已经成为图片分类比较成熟的算法,但是,很少人了解其中的数学原理,这里就先从卷积讲起,后面也会主要到卷积神经网络。希望大家能够很好的理解这个内容,为了以后学习卷积神经网络做准备。
卷积的定义
连续下的定义
(f∗g)(n)=∫f(t)g(n−t)
离散下的定义
(f∗g)(n)=∑f(t)g(n−t)
这里你会发现 括号内的变量加起来岂不就是n, 对的,这就是卷积
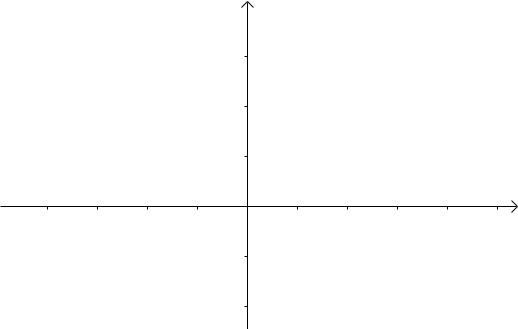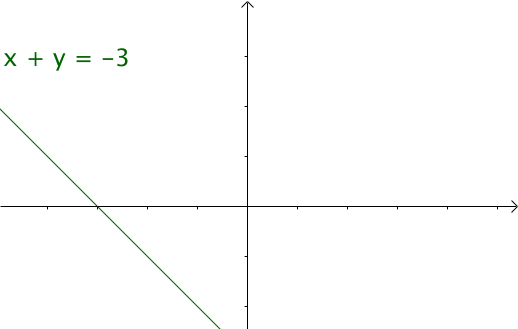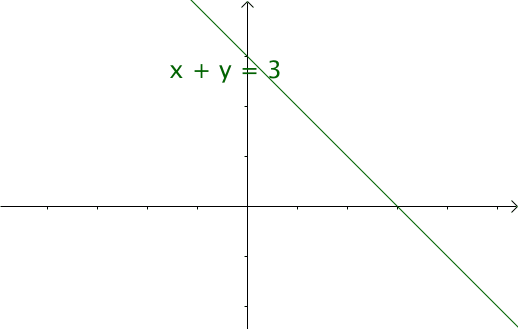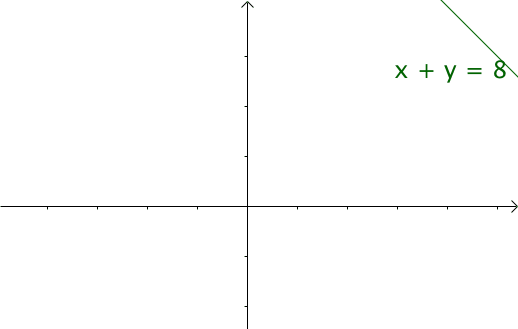
这个就是函数的动画,当然这个图画应该是很多网站都会有的,对的 我是粘贴过来的。
例子
我们考虑一下这种卷积怎么使用呢?
举个栗子
咱们抛两个筛子,结果点数和为4的概率是多少呢:
(f∗g)(n)=∑f(m)g(4−m)
其实我们更关心的是在图像处理中的应用,以为我们将来要学习一个叫做CNN的算法。咱们举个老掉牙的例子吧。
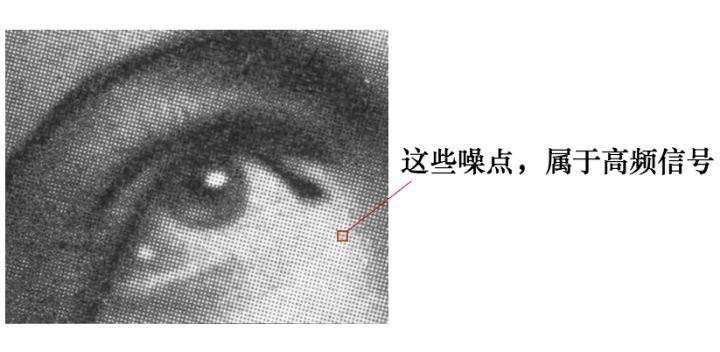
咱们好平滑这些噪点,其实这个可以用数据挖掘的特征理解一下,当数据还有些强特征的时候,反而看一列就能得到分类,这样往往是不好的,这个特征并不是真的强特征。我们希望得到更加泛化的表达。就变成如下的样子。

卷积平滑
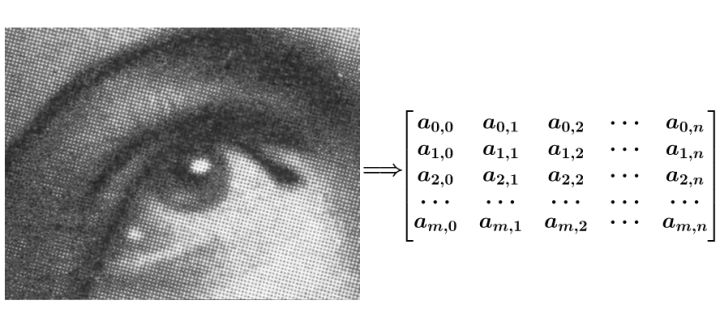
然后用下面这个平均矩阵(说明下,原图的处理实际上用的是正态分布矩阵,这里为了简单,就用了算术平均矩阵)来平滑图像:
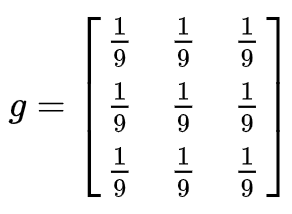
刚才有个问题没有解决,怎么将这些噪声去除呢,一个比较普通的方法就是将噪点分摊给周边的,让他的颜色不要太明显。
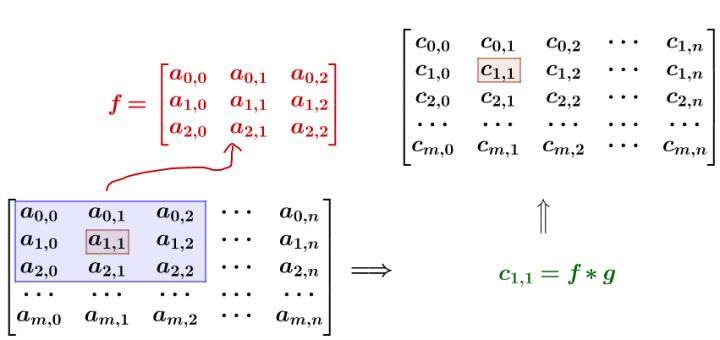
这个即使平滑a1的过程。
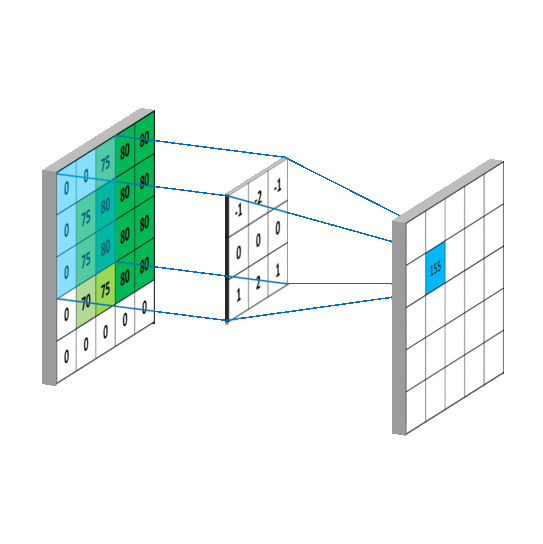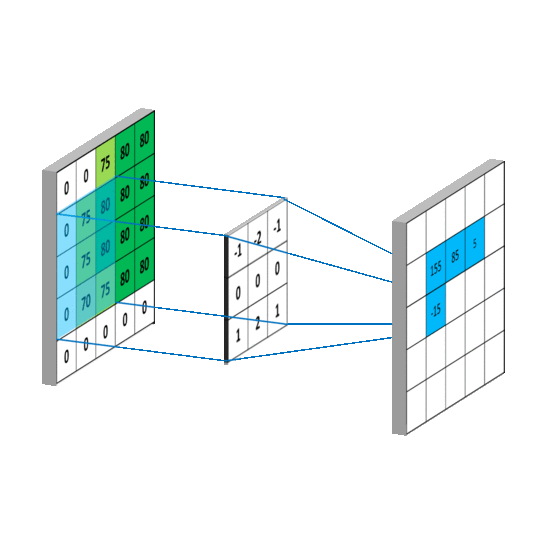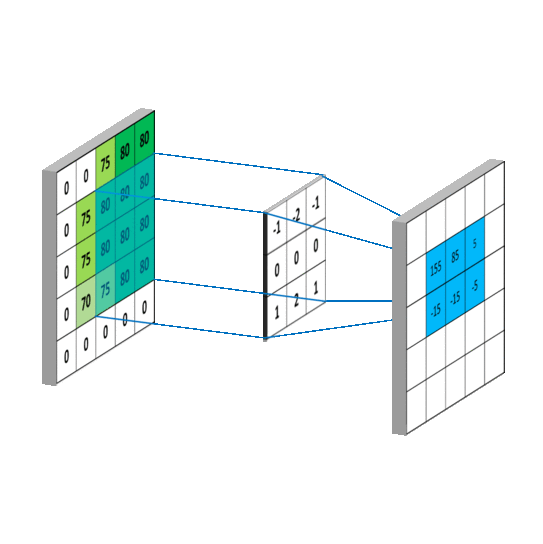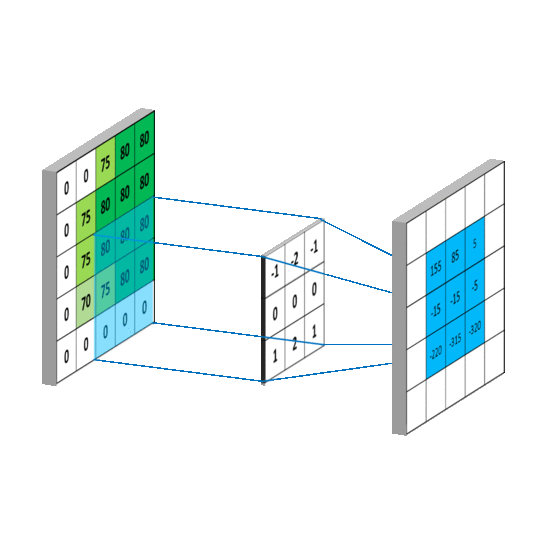
下面这个动图就是平滑的过程,需要说明的是g是上面的平均矩阵,而f是原图的抽取。

写成卷积公式就是:
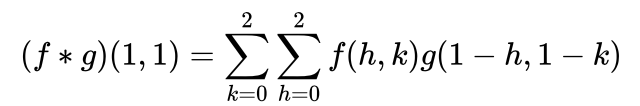
来看一个CNN最喜欢的动图: