#线性规划
本节开始我们就来讲解线性规划问题。看看我们该如何解决带有条件约束的最优解问题。
线性规划简单例子
先从实际问题出发,让我们来了解一下我们将要解决的那种问题?
某制造商生产四种不同的产品,分别用X1,X2,X3,X4来表示,生产过程需要三种原料,其中工作人数和原料等参数如下表,问题当然就是如何保证收益最大。
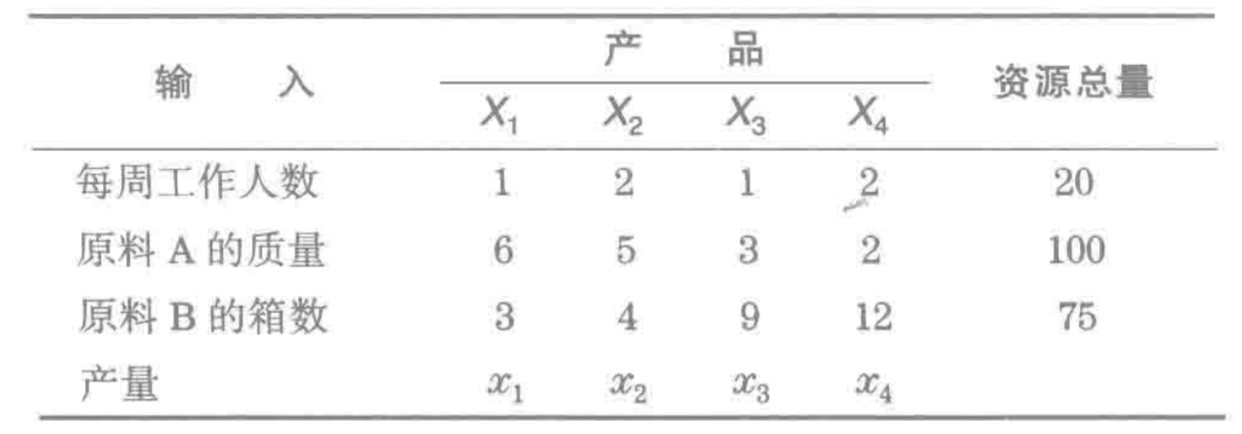
假设产品X1,X2,X3,X4单价分别是6,4,7,5美分,那么对于总收入来说
F=6x1+4x2+7x3+5x4
且需要满足
x1+2x2+x3+x4<=20
6x1+5x2+3x3+2x4<=100
3x1+4x2+9x3+12x4<=20
这样就符合线性优化的基本形式
maxCTx
sbj. Ax<=b
对应我们上面的问题
CT=[6,4,7,5]
后面我们会讲这种问题怎么来获取最优解。
二维线性规划
线性规划很多问题都可以使用二维空间进行说明,因此讨论一般形式的之前,先考虑二维的线性规划的意义。
max CTx
sbj. Ax<=b
x>0
假设
C\^T=[1,5]
w1=[5,6]
w2=[3,2]
A=[w1,w2]\^T
b=[30, 20]\^T
方程组x1+5x2=f,代表一个直线族,当函数f等于某个实数的时,就能确定该问题的一个直线,可以选择x1、x2来找到让原方程最大。
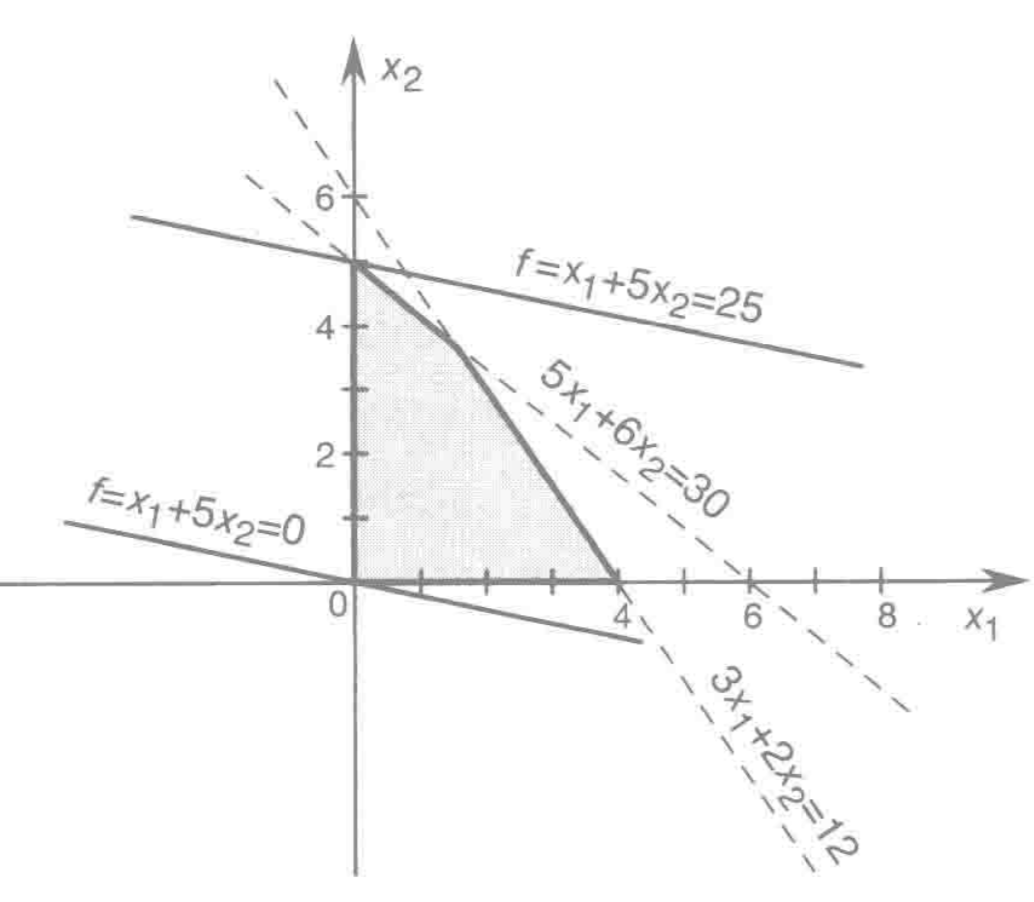
图中阴影的面积就是这个问题的可行域,就是所有可能的取值范围.
这个问题的解是 w=[0,5]
线性规划的标准型
max CTx
sbj. Ax<=b
x>0
以上是线性规划的标准型,很多问题都能够化成标准型然后求解的
如:
考虑优化问题
max x2−x1
sbj. 3x1=x2−5
∣x2∣<=2
x1<=0
转化成标准形:
1.将目标函数变为x1−x2
2.x1=−x1′
3.将∣x2∣<=2转化为x2<=2 和 −x2<=2
4.引入松弛变量[^1][^2] x3和x4,将不等式变为x2+x3=2和−x2+x4=2
5.另x−2=u−v,
那边标准型如下:
min −x1′−u+v
sbj. 3x1′+u−v=5
u−v+x3=2
v−u+x4=2
u,v,x3,x4>=0
基本解
从上面的例子能看看出,任何不等式约束都能够转化成标准型,即问题的线性条件是线性等式,也就是解决标准型的方程。
定义
[xbT,0T] 是Ax=b的基本解,向量xb中的元素称为基变量,B的列向量称为基本列向量。
如果基本解中某些基变量为0,那么这个解称为退化基本解
满足$$Ax=b,x>=0$$的向量称为基本解
如果某个可行解也是基本解,那么就称为基本可行解
如果基本可行解是退化的基本解,那么称为退化基本可行解
其大致的解决方式,往往是利用行列式变换,求解。
结语
下节中我们将聊一聊,这种方程组怎么解。