线性规划
前面铺垫了不少,接下来咱们来看看都怎么解这一堆方程。
矩阵概念
1.如果矩阵E是由单位阵I经过交换矩阵的两行得到的,就是第一类矩阵
2.如果E是由单位阵乘以一个数得到,就叫做第二类矩阵
3.如果E是由单位阵乘以一个数再加到另一行得到的,就叫做第三类矩阵。
定理:对一个矩阵进行第一类、第二类、第三类变换得到的矩阵。相当于对该矩阵乘以一个初等矩阵。
对于
Ax=b
如果A是可逆的,实际上就是求一下等式
x=A−1b
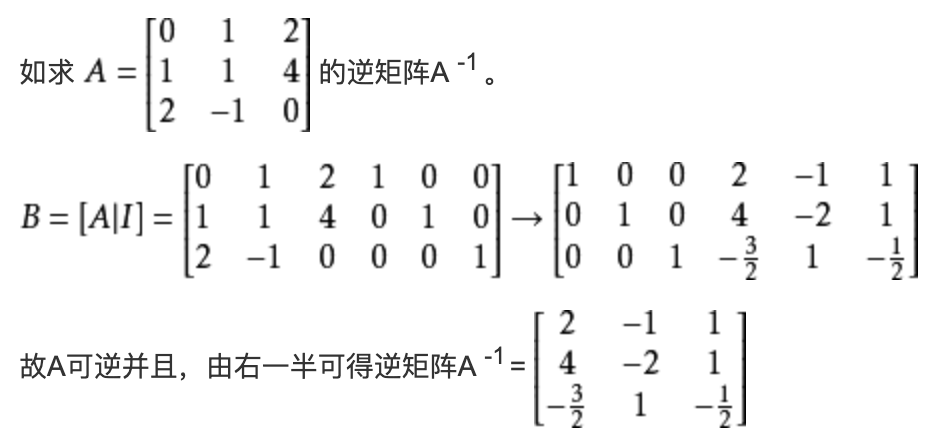
以上就是使用行列式变换来求逆矩阵。
增广矩阵的规范型
所谓的规范形:
[Im,Y1,,,,Yn]
单纯形法
单纯形法基本思路:从一个初始的基本可行解出发,选中一条达到最优基本可行解的最佳途径。
本节并不会多讲,过程比较繁琐但是很容易查到相关资料。
对偶
每个线性规划都有一个与之相对应的一个对偶问题,我们解决对偶问题比较简单。
考虑如下线性规划问题
minimizecTxs.t.Ax>=bx>=0
对偶问题
maximizeλTbs.t.λTA<=cTλ>=0

这里我们一般将遇到的问题的求解转化为解其对偶问题。